Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Đề thi học kì 1 Toán 7 Chân trời sáng tạo - Đề 2

Đề thi cuối kì 1 toán 7 CTST có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 7

Môn: Toán

Dạng tài liệu: Đề thi

Bộ sách: Chân trời sáng tạo

Loại: Tài liệu Lẻ

Loại File: PDF

Phân loại: Tài liệu Tính phí

Đề thi học kì 1 môn Toán 7 - Đề số 2 (sách Chân trời sáng tạo) đi kèm đáp án chi tiết, là tài liệu ôn tập không thể thiếu trong giai đoạn chuẩn bị cho kì thi cuối kì. Đề thi này không chỉ là nguồn ôn luyện chất lượng, giúp các em học sinh củng cố kiến thức và làm quen với cấu trúc đề thi thực tế, mà còn là nguồn tham khảo quan trọng để quý thầy cô xây dựng đề kiểm tra và tổ chức ôn luyện hiệu quả cho học sinh. Mời các bạn tham khảo chi tiết nội dung đề thi ngay dưới đây.

Mời tải về để xem chi tiết.

Đề thi cuối học kì 1 Toán 7 Chân trời sáng tạo

I. PHẦN TRẮC NGHIỆM: (3,0 điểm)

Khoanh vào chữ cái đặt trước câu trả lời đúng.

Câu 1: Trong các câu sau, câu nào sai?

A. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương

B. Số tư nhiên hớn hơn số hữu tỉ âm

C. Số nguyên âm không phải là số hữu tỉ

D. Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm

Câu 2: Số đối của số hữu tỉ $\frac{-1}{12}$ $\frac{-1}{12}$ là

A. 12;

B. $-\frac{1}{12}$ $-\frac{1}{12}$;

C. $\frac{1}{12}$ $\frac{1}{12}$;

D. −12.

Câu 3: Căn bậc hai số học của 25 là

A. −5;

B. ±5;

C. $-\sqrt{25}$ $-\sqrt{25}$;

D. 5.

Câu 4: Số $\sqrt{3}$ $\sqrt{3}$ thuộc tập hợp số nào sau đây?

A. ℤ;

B. 𝕀;

C. ℚ;

D. ℕ.

Câu 5: Cho điểm M nằm ngoài đường thẳng d. Có bao nhiêu đường thẳng qua M và song song với d?

A. 0;

B. 1;

C. 2;

D. vô số.

Câu 6: Cho lăng trụ đứng có kích thước như hình vẽ.

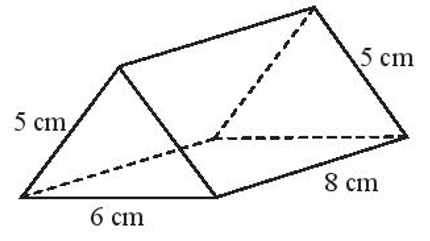
Số nào trong các số sau đây là diện tích xung quanh của hình lăng trụ đứng đó?

A. 120 cm²;

B. 24 cm²;

C. 128 cm²;

D. 200 cm².

Câu 7: Một hình lăng trụ đứng tứ giác có độ dài cạnh bên là 20cm và đáy là hình thoi với độ dài hai đường chéo là 18cm;30cm. Tính thể tích của hình lăng trụ đó.

A. $6\,300\,c{m^3}$ $6\,300\,c{m^3}$

B. $5\,400\,c{m^3}$ $5\,400\,c{m^3}$

C. $3\,600c{m^3}$ $3\,600c{m^3}$

D. $4\,800\,c{m^3}$ $4\,800\,c{m^3}$

Câu 8: Trong các câu sau, câu nào cho một định lí?

A. Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia;

B. Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia;

C. Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song;

D. Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.

Câu 9: Biểu đồ dưới đây cho biết tỉ số phần trăm diện tích trồng các loại cây ăn quả ở một trang trại.

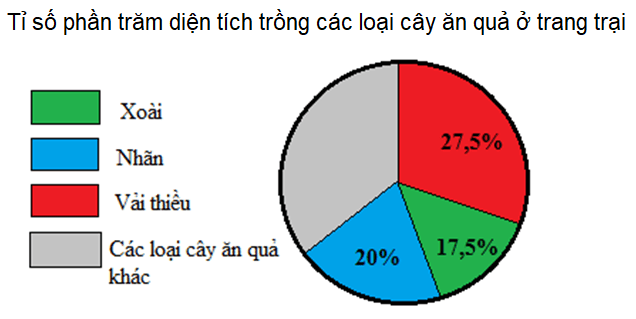
Căn cứ vào biểu đồ sau đây, hãy cho biết tỉ số phần trăm diện tích trồng các loại cây ăn quả khác là bao nhiêu?

A. 27,5%;

B. 20%;

C. 17,5%;

D. 35%.

Câu 10: Cho biểu đồ sau:

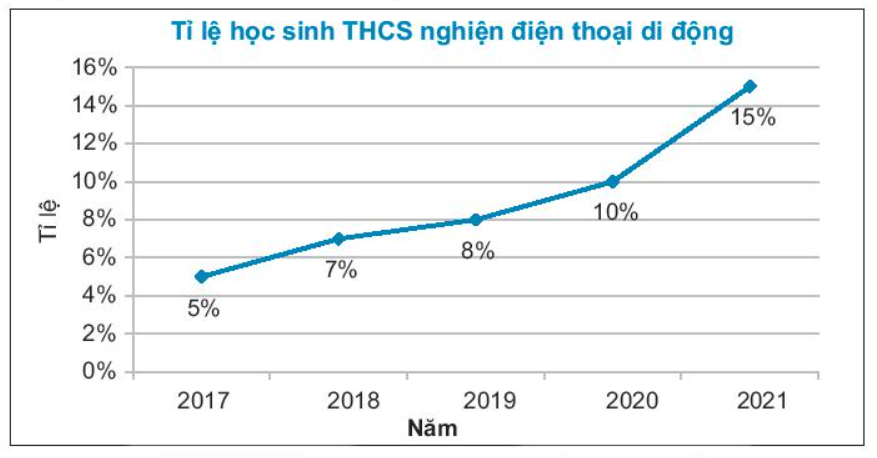
Năm nào có tỉ lệ học sinh THCS nghiện điện thoại cao nhất?

A. 2021;

B. 2020;

C. 2019;

D. 2018.

Phần II. Tự luận (7 điểm):

Bài 1: (2,0 điểm)

Tính hợp lí (nếu có thể):

a) $\dfrac{{ - 15}}{{14}}:\dfrac{{17}}{{23}} - \dfrac{{15}}{{14}}:\dfrac{{17}}{{11}} - \dfrac{6}{7}$ $\dfrac{{ - 15}}{{14}}:\dfrac{{17}}{{23}} - \dfrac{{15}}{{14}}:\dfrac{{17}}{{11}} - \dfrac{6}{7}$

b) $\left( {\dfrac{{ - 5}}{3} + \dfrac{{ - 3}}{2}} \right):\dfrac{{17}}{{13}} + \left( {\dfrac{7}{2} + \dfrac{{ - 1}}{3}} \right):\dfrac{{17}}{{13}}$ $\left( {\dfrac{{ - 5}}{3} + \dfrac{{ - 3}}{2}} \right):\dfrac{{17}}{{13}} + \left( {\dfrac{7}{2} + \dfrac{{ - 1}}{3}} \right):\dfrac{{17}}{{13}}$

c) ${3^2}.\dfrac{1}{{243}}{.81^2}.\dfrac{1}{{{3^3}}}$ ${3^2}.\dfrac{1}{{243}}{.81^2}.\dfrac{1}{{{3^3}}}$

d) $\left( {{{4.2}^5}} \right):\left( {{2^3}.\dfrac{1}{{16}}} \right)$ $\left( {{{4.2}^5}} \right):\left( {{2^3}.\dfrac{1}{{16}}} \right)$

Bài 2: (2,0 điểm)

Tìm x, biết:

a) $\left( { - 0,2} \right) - x.\dfrac{1}{6} = \dfrac{2}{3}$ $\left( { - 0,2} \right) - x.\dfrac{1}{6} = \dfrac{2}{3}$

b) $\left( {\dfrac{1}{3}x - \dfrac{8}{{13}}} \right).\left( {2,5 + \dfrac{{ - 7}}{5}:x} \right) = 0$ $\left( {\dfrac{1}{3}x - \dfrac{8}{{13}}} \right).\left( {2,5 + \dfrac{{ - 7}}{5}:x} \right) = 0$

c) $5.\left( {\dfrac{1}{{\sqrt {25} }} - x} \right) - \sqrt {\dfrac{1}{{81}}} = \dfrac{{ - 1}}{9}$ $5.\left( {\dfrac{1}{{\sqrt {25} }} - x} \right) - \sqrt {\dfrac{1}{{81}}} = \dfrac{{ - 1}}{9}$

d) $\left| x \right| - \dfrac{{23}}{{17}} = 0$ $\left| x \right| - \dfrac{{23}}{{17}} = 0$

Bài 3: (1,5 điểm)

Một chiếc khay nhựa đựng đồ có dạng hình hộp chữ nhật như hình vẽ bên dưới.

Dựa vào kích thước trên hình (coi mép khay nhựa không đáng kể), hãy tỉnh:

a) Diện tích xung quanh của chiếc khay.

b) Diện tích nhựa để làm chiếc khay trên.

c) Thể tích nước khay nhựa có thể chứa được.

Bài 4: (1,0 điểm)

Chi phí xây dựng nhà được biểu diễn qua biểu đồ hình quạt tròn sau:

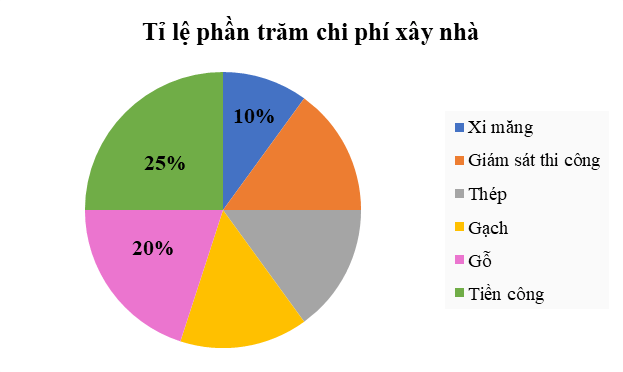
a) Tính số phần trăm chi phí gạch. Biết rằng chi phí giám sát thi công, thép, gạch bằng nhau.

b) Biết rằng để xây dựng một ngôi nhà bác An đã chi trả hết 2,5 tỉ đồng. Hỏi chi phí trả tiền công là bao nhiêu?

Bài 5: (0,5 điểm)

Cho hai góc có cạnh tương ứng song song cùng nhọn hoặc cùng tù. Biết hai tia phân giác của chúng không cùng nằm trên một đường thẳng. Chứng minh rằng hai tia phân giác này song song với nhau.

***************

Tải về

Chọn file muốn tải về: