Giải Toán lớp 6 Bài 15: Phân tích một số ra thừa số nguyên tố
Giải bài tập trang 50, 51 SGK Toán lớp 6 tập 1: Phân tích một số ra thừa số nguyên tố với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán lớp 6. Lời giải bài tập Toán 6 gồm các bài giải tương ứng với từng bài học trong sách giúp cho các em học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán.
Giải bài tập Toán lớp 6: Phân tích một số ra thừa số nguyên tố
- A. Lý thuyết phân tích ra thừa số nguyên tố
- B. Giải Toán lớp 6 tập 1 trang 50, 51
- Câu hỏi trang 50 SGK Toán 6 tập 1
- Bài 125 trang 50 SGK Toán 6 tập 1
- Bài 126 trang 50 SGK Toán 6 tập 1
- Bài 127 trang 50 SGK Toán 6 tập 1
- Bài 128 trang 50 SGK Toán 6 tập 1
- Bài 129 trang 50 SGK Toán 6 tập 1
- Bài 130 trang 50 SGK Toán 6 tập 1
- Bài 131 trang 50 Toán SGK 6 tập 1
- Bài 132 trang 51 SGK Toán 6 tập 1
- Bài 133 trang 51 SGK Toán 6 tập 1
A. Lý thuyết phân tích ra thừa số nguyên tố
+ Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
*Lưu ý:
+ Dạng phân tích ra thừa số nguyên tố của mỗi số nguyên tố là chính nó.
+ Mọi hợp số đều phân tích được ra thừa số nguyên tố.
* Muốn phân tích một số tự nhiên a lớn hơn 1 ra thừa số nguyên tố ta có thể làm như sau:
+ Kiểm tra xem 2 có phải là ước của a hay không. Nếu không ta xét số nguyên tố 3 và cứ như thế đối với các số nguyên tố lớn dần.
+ Giả sử p là ước nguyên tố nhỏ nhất của a, ta chia a cho p được thương b.
+ Tiếp tục thực hiện quy trình trên đối với b.
+ Quá trình trên kéo dài cho đến khi ta được thương là 1.
* Lưu ý:
+ Dù phân tích một số tự nhiên ra thừa số nguyên tố bằng cách nào thì cũng được cùng một kết quả.
+ Trong cách phân tích một số ra thừa số nguyên tố, ta thường viết các ước nguyên tố theo thứ tự từ nhỏ đến lớn.
B. Giải Toán lớp 6 tập 1 trang 50, 51
Câu hỏi trang 50 SGK Toán 6 tập 1
Phân tích số 420 ra thừa số nguyên tố:
Hướng dẫn:
* Muốn phân tích một số tự nhiên a lớn hơn 1 ra thừa số nguyên tố ta có thể làm như sau:
+ Kiểm tra xem 2 có phải là ước của a hay không. Nếu không ta xét số nguyên tố 3 và cứ như thế đối với các số nguyên tố lớn dần.
+ Giả sử p là ước nguyên tố nhỏ nhất của a, ta chia a cho p được thương b.
+ Tiếp tục thực hiện quy trình trên đối với b.
+ Quá trình trên kéo dài cho đến khi ta được thương là 1.
Lời giải:
Ta có:
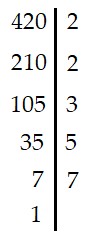 | Vậy 420 = 2.2.3.5.7 = 22.3.5.7 |
Bài 125 trang 50 SGK Toán 6 tập 1
Phân tích các số sau ra thừa số nguyên tố:
| a) 60 | b) 84; | c) 285; |
| d) 1035; | e) 400; | g) 1000000 |
Hướng dẫn:
* Muốn phân tích một số tự nhiên a lớn hơn 1 ra thừa số nguyên tố ta có thể làm như sau:
+ Kiểm tra xem 2 có phải là ước của a hay không. Nếu không ta xét số nguyên tố 3 và cứ như thế đối với các số nguyên tố lớn dần.
+ Giả sử p là ước nguyên tố nhỏ nhất của a, ta chia a cho p được thương b.
+ Tiếp tục thực hiện quy trình trên đối với b.
+ Quá trình trên kéo dài cho đến khi ta được thương là 1.
Lời giải:
a) 60
Ta có:
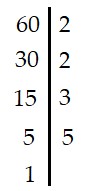 | Vậy 60 = 2.2.3.5 = 22.3.5 |
b) 84
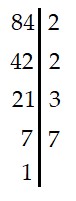 | Vậy 84 = 2.2.3.7 = 22.3.7 |
c) 285
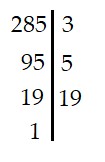 | Vậy 285 = 3.5.19 |
d) 1035
 | Vậy 1035 = 3.3.5.23 = 32.5.23 |
e) 400
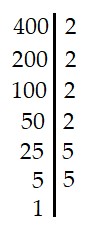 | Vậy 400 = 2.2.2.2.5.5 = 24.52 |
g) 1 000 000
Ta có: 1 000 000 = 10.10.10.10.10.10.10
Vậy 1 000 000 = (2.5).(2.5).(2.5).(2.5).(2.5).(2.5) = 26.56
Bài 126 trang 50 SGK Toán 6 tập 1
An phân tích các số 120, 306, 567 ra thừa số nguyên tố như sau:
120 = 2.3.4.5
306 = 2.3.51
567 = 92.7
An làm như trên có đúng không? Hãy sửa lại trong trường hợp An làm không đúng.
Hướng dẫn:
+ Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
Lời giải:
+ An làm không đúng vì chưa phân tích hết ra thừa số nguyên tố. Chẳng hạn, 4, 51, 9 không phải là các số nguyên tố.
+ Sửa lại:
120 = 2.3.4.5 = 2.3.2.2.5 = 23.3.5
306 = 2.3.51 = 2.3.3.17 = 2.32.17
567 = 92.7 = 9.9.7 = 3.3.3.3.7 = 34.7
Bài 127 trang 50 SGK Toán 6 tập 1
Phân tích các số sau ra thừa số nguyên tố rồi cho biết mỗi số đó chia hết cho các số nguyên tố nào?
| a) 225 | b) 1800 | c) 1050 | d) 3060 |
Hướng dẫn:
* Muốn phân tích một số tự nhiên a lớn hơn 1 ra thừa số nguyên tố ta có thể làm như sau:
+ Kiểm tra xem 2 có phải là ước của a hay không. Nếu không ta xét số nguyên tố 3 và cứ như thế đối với các số nguyên tố lớn dần.
+ Giả sử p là ước nguyên tố nhỏ nhất của a, ta chia a cho p được thương b.
+ Tiếp tục thực hiện quy trình trên đối với b.
+ Quá trình trên kéo dài cho đến khi ta được thương là 1.
Lời giải:
a) 225
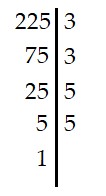 | Vậy 225 = 3.3.5.5 = 32.52 225 chia hết cho 2 và 5 |
b) 1800
 | Vậy 1800 = 2.2.2.3.3.5.5 = 23.32.52 1800 chia hết cho 2; 3 và 5 |
c) 1050
 | Vậy 1050 = 2.3.5.5.7 = 2.3.52.7 1050 chia hết cho 2; 3; 5 và 7 |
d) 3060
 | Vậy 3060 = 2.2.3.3.5.17 = 22.32.5.17 3060 chia hết cho 2; 3; 5 và 17 |
Bài 128 trang 50 SGK Toán 6 tập 1
Cho số a = 23.52.11. Mỗi số 4, 8, 16, 11, 20 có là ước của a hay không?
Hướng dẫn:
+ Nếu số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b, còn b gọi là ước của a.
Lời giải:
+ Có 23.52.11 = 2.2.2.52.11 = 4.2.52.11 ⋮ 4 nên 4 là ước của a.
+ Có 23.52.11 = 2.2.2.52.11 = 8.52.11 ⋮ 8 nên 8 là ước của a.
+ Vì 16 = 24 mà a chia hết cho lũy thừa cao nhất của 2 là 23 nên 16 không là ước của a.
+ Có 23.52.11 ⋮ 11 nên 11 là ước của a.
+ Có 23.52.11 = 2.2.2.5.5.11 = 2.20.5.11 ⋮ 20 nên 20 là ước của a.
Bài 129 trang 50 SGK Toán 6 tập 1
a) Cho số a = 5.13. Hãy viết tất cả các ước của a.
b) Cho số b = 25 . Hãy viết tất cả các ước của b.
c) Cho số c = 32.7. Hãy viết tất cả các ước của c.
Hướng dẫn:
+ Nếu số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b, còn b gọi là ước của a.
+ Muốn tìm các ước của một tích m.n ta tìm các ước của m, của n và tích của mỗi ước của m với một ước của n.
Lời giải:
a) a = 5.13 có các ước là 1, 5, 13 và 5.13 = 65. Vậy Ư(a) = {1; 5; 13; 65}
b) Các ước của 25 là 1, 2, 22, 23, 24, 25. Vậy Ư(b) = {1; 2; 4; 8; 16; 32}
c) Các ước của 32.7 là 1, 3, 32, 7, 3.7, 32.7. Vậy Ư(c) = {1; 3; 7; 9; 21; 63}
Bài 130 trang 50 SGK Toán 6 tập 1
Phân tích các số sau ra thừa số nguyên tố rồi tìm tập hợp các ước của mỗi số:
51; 75; 42; 30.
Hướng dẫn:
* Muốn phân tích một số tự nhiên a lớn hơn 1 ra thừa số nguyên tố ta có thể làm như sau:
+ Kiểm tra xem 2 có phải là ước của a hay không. Nếu không ta xét số nguyên tố 3 và cứ như thế đối với các số nguyên tố lớn dần.
+ Giả sử p là ước nguyên tố nhỏ nhất của a, ta chia a cho p được thương b.
+ Tiếp tục thực hiện quy trình trên đối với b.
+ Quá trình trên kéo dài cho đến khi ta được thương là 1.
* Nếu số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b, còn b gọi là ước của a.
Lời giải:
* Số 51
Ta có:
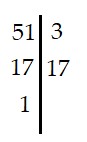 | Vậy 51 = 3.17 → Ư(51) = {1; 3; 17; 51} |
* Số 75
Ta có:
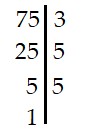 | Vậy 75 = 3.5.5 = 3.52 → Ư(75) = {1; 3; 5; 15; 25; 75} |
* Số 42
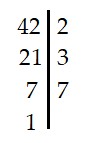 | Vậy 42 = 2.3.7 → Ư(42) = {1; 2; 3; 6; 7; 14; 21; 42} |
* Số 30
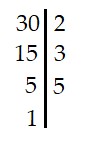 | Vậy 30 = 2.3.5 → Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30} |
Bài 131 trang 50 Toán SGK 6 tập 1
a) Tích của hai số tự nhiên bằng 42. Tìm mỗi số.
b) Tích của hai số tự nhiên a và b bằng 30. Tìm a và b, biết rằng a < b.
Hướng dẫn:
+ Viết tập hợp ước của hai số 42 và 30. Từ đó tìm các cặp số thỏa mãn bài toán.
Lời giải:
a) Gọi hai số tự nhiên có tích bằng 42 là a và b (a, b > 0)
Có 42 = a.b nên a, b ∈ Ư(42) = {1; 2; 3; 6; 7; 14; 21; 42}
Ta có bảng:
| Giá trị a | 1 | 2 | 3 | 6 | 7 | 14 | 21 | 42 |
| Giá trị b | 42 | 21 | 14 | 7 | 6 | 3 | 2 | 1 |
b) Gọi hai số tự nhiên có tích bằng 42 là a và b (b > a > 0)
Có 30 = a.b nên a, b ∈ Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}
Ta có bảng:
| Giá trị a | 1 | 2 | 3 | 5 | 6 | 10 | 15 | 30 |
| Giá trị b | 30 | 15 | 10 | 6 | 5 (loại) | 3 (loại) | 2 (loại) | 1 (loại) |
Bài 132 trang 51 SGK Toán 6 tập 1
Tâm có 28 viên bi. Tâm muốn xếp số bi đó vào túi sao cho số bi ở các túi đều bằng nhau. Hỏi Tâm có thể xếp 28 viên bi đó vào mấy túi ? (kể cả trường hợp xếp vào một túi).
Hướng dẫn:
+ Số bi ở mỗi túi đều bằng nhau nên số bi ở mỗi túi và số túi đều thuộc tập ước của 28.
+ Ta tìm tập ước của 28 để tìm số bi ở mỗi túi và số túi.
Lời giải:
+ Vì số bi ở các túi bằng nhau nên số túi phải là ước của 28.
+ Ta có 28 = 4.7 = 22.7. Suy ra Ư(28) = {1; 2; 4; 7; 14; 28}.
+ Vậy số túi có thể là: 1; 2; 4; 7; 14; 28 túi
Bài 133 trang 51 SGK Toán 6 tập 1
a) Phân tích số 111 ra thừa số nguyên tố rồi tìm tập hợp các ước của 111.
b) Thay dấu * bởi chữ số thích hợp: 
\(\overline {**} .* = 111\)
Hướng dẫn:
* Muốn phân tích một số tự nhiên a lớn hơn 1 ra thừa số nguyên tố ta có thể làm như sau:
+ Kiểm tra xem 2 có phải là ước của a hay không. Nếu không ta xét số nguyên tố 3 và cứ như thế đối với các số nguyên tố lớn dần.
+ Giả sử p là ước nguyên tố nhỏ nhất của a, ta chia a cho p được thương b.
+ Tiếp tục thực hiện quy trình trên đối với b.
+ Quá trình trên kéo dài cho đến khi ta được thương là 1.
Lời giải:
a) Ta có:
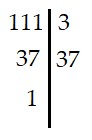 | Vậy 111 = 3.37 → Ư(111) = {1; 3; 37; 111} |
b) Vì \(\overline {**} .* = 111\) nên \(\overline {**}\) và * đều là các ước của 111
\(\overline {**}\) có hai chữ số, mà ước có hai chữ số của 111 là 37 nên \(\overline {**} = 37\) và * = 3
-----------
Bài tiếp theo: Giải bài tập Toán 6 trang 53, 54 SGK tập 1: Ước chung và bội chung
Ngoài ra các em học sinh có thể tham khảo các bài giải SGK môn Toán lớp 6, Môn Ngữ văn 6, Môn Vật lý 6, môn Sinh Học 6, Lịch sử 6, Địa lý 6....và các đề thi học kì 1 lớp 6 và đề thi học kì 2 lớp 6 để chuẩn bị cho các bài thi đề thi học kì đạt kết quả cao.
Tham khảo các dạng bài tập Toán 6:
