Giải Toán lớp 6 bài 4: Rút gọn phân số

Giải bài tập môn Toán lớp 6

Giải Toán lớp 6 tập 2 trang 15, 16: Rút gọn phân số

A. Lý thuyết rút gọn phân số
- 1. Cách rút gọn phân số
- 2. Phân số tối giản
B. Giải bài tập SGK Toán lớp 6 tập 2 trang 15, 16

Giải bài tập SGK Toán lớp 6 Đại số Chương 3 bài 4: Rút gọn phân số sẽ giúp các em học sinh định hướng và gợi ý cách giải các bài tập trang 15, 16 môn Toán lớp 6 tập 2 nhằm giúp các em ôn tập và nắm vững hơn nội dung chính của bài học. Bên cạnh đó, việc tham khảo tài liệu còn giúp các em dễ dàng hoàn thiện bài tập của mình, nắm được cách giải để vận dụng vào giải các bài tập liên quan đến phân số.

A. Lý thuyết rút gọn phân số

1. Cách rút gọn phân số

Muốn rút gọn phân số ta chia cả tử và mẫu của phân số cho một ước chung (khác 1 và -1) của chúng.

2. Phân số tối giản

Phân số tối giản (hay phân số không rút gọn được nữa) là phân số mà tử và mẫu chỉ có một ước chung là 1 và -1.

Để rút gọn phân số về phân số tối giản, ta chia tử số và mẫu số của phân số cho ƯCLN của tử số và mẫu số phân số đó.

B. Giải bài tập SGK Toán lớp 6 tập 2 trang 15, 16

Bài 15 trang 15 SGK Toán 6 tập 2

Rút gọn các phân số sau:

a) $\frac{{22}}{{55}}$ $\frac{{22}}{{55}}$

b) $\frac{{ - 63}}{{81}}$ $\frac{{ - 63}}{{81}}$

c) $\frac{{20}}{{ - 140}}$ $\frac{{20}}{{ - 140}}$

d) $\frac{{ - 25}}{{ - 75}}$ $\frac{{ - 25}}{{ - 75}}$

Hướng dẫn:

Muốn rút gọn phân số ta chia cả tử và mẫu của phân số cho một ước chung (khác 1 và -1) của chúng.

Lời giải:

a) $\frac{{22}}{{55}} = \frac{{22:11}}{{55:11}} = \frac{2}{5}$ $\frac{{22}}{{55}} = \frac{{22:11}}{{55:11}} = \frac{2}{5}$

b) $\frac{{ - 63}}{{81}} = \frac{{\left( { - 63} \right):9}}{{81:9}} = \frac{{ - 7}}{9}$ $\frac{{ - 63}}{{81}} = \frac{{\left( { - 63} \right):9}}{{81:9}} = \frac{{ - 7}}{9}$

c) $\frac{{20}}{{ - 140}} = \frac{{20:\left( { - 20} \right)}}{{\left( { - 140} \right):\left( { - 20} \right)}} = \frac{{ - 1}}{7}$ $\frac{{20}}{{ - 140}} = \frac{{20:\left( { - 20} \right)}}{{\left( { - 140} \right):\left( { - 20} \right)}} = \frac{{ - 1}}{7}$

d) $\frac{{ - 25}}{{ - 75}} = \frac{{\left( { - 25} \right):\left( { - 25} \right)}}{{\left( { - 75} \right):\left( { - 25} \right)}} = \frac{1}{3}$ $\frac{{ - 25}}{{ - 75}} = \frac{{\left( { - 25} \right):\left( { - 25} \right)}}{{\left( { - 75} \right):\left( { - 25} \right)}} = \frac{1}{3}$

Bài 16 trang 15 SGK Toán 6 tập 2

Bộ răng đầy đủ của một người trưởng thành có 32 chiếc trong đó có 8 răng cửa, 4 răng nanh, 8 răng cối nhỏ và 12 răng hàm. Hỏi mỗi loại răng chiếm mấy phần của tổng số răng (Viết dưới dạng phân số).

Hướng dẫn:

Muốn rút gọn phân số ta chia cả tử và mẫu của phân số cho một ước chung (khác 1 và -1) của chúng.

Lời giải:

Có: $\frac{8}{{32}} = \frac{{8:8}}{{32:8}} = \frac{1}{4};\,\,\,\frac{4}{{32}} = \frac{{4:4}}{{32:4}} = \frac{1}{8};\,\,\,\frac{{12}}{{32}} = \frac{{12:4}}{{32:4}} = \frac{3}{8}$ $\frac{8}{{32}} = \frac{{8:8}}{{32:8}} = \frac{1}{4};\,\,\,\frac{4}{{32}} = \frac{{4:4}}{{32:4}} = \frac{1}{8};\,\,\,\frac{{12}}{{32}} = \frac{{12:4}}{{32:4}} = \frac{3}{8}$

Vậy răng cửa chiếm $\frac{1}{4}$ $\frac{1}{4}$ tổng số răng.

Răng nanh chiếm $\frac{1}{8}$ $\frac{1}{8}$ tổng số răng.

Răng cối nhỏ chiếm $\frac{1}{4}$ $\frac{1}{4}$ tổng số răng.

Răng hàm chiếm $\frac{3}{8}$ $\frac{3}{8}$ tổng số răng

Bài 17 trang 15 SGK Toán 6 tập 2

Rút gọn:

a) $\frac{{3.5}}{{8.24}}$ $\frac{{3.5}}{{8.24}}$	b) $\frac{{2.14}}{{7.8}}$ $\frac{{2.14}}{{7.8}}$	c) $\frac{{3.7.11}}{{22.9}}$ $\frac{{3.7.11}}{{22.9}}$
d) $\frac{{8.5 - 8.2}}{{16}}$ $\frac{{8.5 - 8.2}}{{16}}$	e) $\frac{{11.4 - 11}}{{2 - 13}}$ $\frac{{11.4 - 11}}{{2 - 13}}$

Hướng dẫn:

Ta có thể phân tích tử và mẫu của phân số ra thừa số nguyên tố rồi chia cả tử và mẫu cho thừa số chung.

Lời giải:

a) $\frac{{3.5}}{{8.24}} = \frac{{3.5}}{{8.8.3}} = \frac{5}{{8.8}} = \frac{5}{{64}}$ $\frac{{3.5}}{{8.24}} = \frac{{3.5}}{{8.8.3}} = \frac{5}{{8.8}} = \frac{5}{{64}}$

b) $\frac{{2.14}}{{7.8}} = \frac{{2.2.7}}{{7.2.2.2}} = \frac{1}{2}$ $\frac{{2.14}}{{7.8}} = \frac{{2.2.7}}{{7.2.2.2}} = \frac{1}{2}$

c) $\frac{{3.7.11}}{{22.9}} = \frac{{3.7.11}}{{2.11.3.3}} = \frac{7}{{2.3}} = \frac{7}{6}$ $\frac{{3.7.11}}{{22.9}} = \frac{{3.7.11}}{{2.11.3.3}} = \frac{7}{{2.3}} = \frac{7}{6}$

d) $\frac{{8.5 - 8.2}}{{16}} = \frac{{8.\left( {5 - 2} \right)}}{{8.2}} = \frac{{8.3}}{{8.2}} = \frac{3}{2}$ $\frac{{8.5 - 8.2}}{{16}} = \frac{{8.\left( {5 - 2} \right)}}{{8.2}} = \frac{{8.3}}{{8.2}} = \frac{3}{2}$

e) $\frac{{11.4 - 11}}{{2 - 13}} = \frac{{11.\left( {4 - 1} \right)}}{{ - 11}} = \frac{{11.3}}{{ - 11}} = \frac{3}{{ - 1}} = - 3$ $\frac{{11.4 - 11}}{{2 - 13}} = \frac{{11.\left( {4 - 1} \right)}}{{ - 11}} = \frac{{11.3}}{{ - 11}} = \frac{3}{{ - 1}} = - 3$

Bài 18 trang 15 SGK Toán 6 tập 2

Viết các số đo thời gian sau đây với đơn vị là giờ (chú ý rút gọn nếu có thể):

a) 20 phút

b) 35 phút

c) 90 phút.

Hướng dẫn :

Vì 1 giờ = 60 phút nên 1 phút = $\frac{1}{{60}}$ $\frac{1}{{60}}$ giờ

Muốn rút gọn phân số ta chia cả tử và mẫu của phân số cho một ước chung (khác 1 và -1) của chúng.

Lời giải

a) 20 phút = $\frac{{20}}{{60}}$ $\frac{{20}}{{60}}$ giờ = $\frac{1}{3}$ $\frac{1}{3}$ giờ

b) 35 phút = $\frac{{35}}{{60}}$ $\frac{{35}}{{60}}$ giờ = $\frac{7}{{12}}$ $\frac{7}{{12}}$ giờ

c) 90 phút = $\frac{{90}}{{60}}$ $\frac{{90}}{{60}}$ giờ = $\frac{3}{2}$ $\frac{3}{2}$giờ

Bài 19 trang 15 SGK Toán 6 tập 2

Đổi ra mét vuông (viết dưới dạng phân số tối giản):

25 dm² 36 dm² 450 cm² 575 cm²

Hướng dẫn:

Có 1m² = 100 dm² = 10000 cm²

Muốn rút gọn phân số ta chia cả tử và mẫu của phân số cho một ước chung (khác 1 và -1) của chúng.

Lời giải:

Có:

25dm²= $\frac{{25}}{{100}}$ $\frac{{25}}{{100}}$m² = $\frac{1}{4}$ $\frac{1}{4}$m²

36dm² = $\frac{{36}}{{100}}$ $\frac{{36}}{{100}}$m² = $\frac{9}{{25}}$ $\frac{9}{{25}}$m²

450cm² = $\frac{{450}}{{10000}}$ $\frac{{450}}{{10000}}$m² = $\frac{9}{{200}}$ $\frac{9}{{200}}$m²

575cm² = $\frac{{575}}{{10000}}$ $\frac{{575}}{{10000}}$m² = $\frac{{23}}{{400}}$ $\frac{{23}}{{400}}$m²

Bài 20 trang 15 SGK Toán 6 tập 2

Tìm các cặp phân số bằng nhau trong các phân số sau đây:

$\frac{{ - 9}}{{33}};\,\,\,\frac{{15}}{9};\,\,\,\frac{3}{{ - 11}};\,\,\,\frac{{ - 12}}{{19}};\,\,\,\frac{5}{3};\,\,\,\frac{{60}}{{ - 95}}$ $\frac{{ - 9}}{{33}};\,\,\,\frac{{15}}{9};\,\,\,\frac{3}{{ - 11}};\,\,\,\frac{{ - 12}}{{19}};\,\,\,\frac{5}{3};\,\,\,\frac{{60}}{{ - 95}}$

Hướng dẫn:

Rút gọn các phân số về phân số tối giản để tìm các phân số bằng nhau.

Lời giải:

Có:

$\frac{{ - 9}}{{33}} = \frac{{\left( { - 9} \right):\left( { - 3} \right)}}{{33:\left( { - 3} \right)}} = \frac{3}{{ - 11}}$ $\frac{{ - 9}}{{33}} = \frac{{\left( { - 9} \right):\left( { - 3} \right)}}{{33:\left( { - 3} \right)}} = \frac{3}{{ - 11}}$

$\frac{{15}}{9} = \frac{{15:3}}{{9:3}} = \frac{5}{3}$ $\frac{{15}}{9} = \frac{{15:3}}{{9:3}} = \frac{5}{3}$

$\frac{{60}}{{ - 95}} = \frac{{60:\left( { - 5} \right)}}{{\left( { - 95} \right):\left( { - 5} \right)}} = \frac{{ - 12}}{{19}}$ $\frac{{60}}{{ - 95}} = \frac{{60:\left( { - 5} \right)}}{{\left( { - 95} \right):\left( { - 5} \right)}} = \frac{{ - 12}}{{19}}$

Bài 21 trang 15 SGK Toán 6 tập 2

Trong các phân số sau đây, tìm phân số không bằng phân số nào trong các phân số còn lại:

$\frac{{ - 7}}{{42}};\,\,\,\frac{{12}}{{18}};\,\,\,\frac{3}{{ - 18}};\,\,\,\frac{{ - 9}}{{54}};\,\,\,\frac{{ - 10}}{{ - 15}};\,\,\,\frac{{14}}{{20}}$ $\frac{{ - 7}}{{42}};\,\,\,\frac{{12}}{{18}};\,\,\,\frac{3}{{ - 18}};\,\,\,\frac{{ - 9}}{{54}};\,\,\,\frac{{ - 10}}{{ - 15}};\,\,\,\frac{{14}}{{20}}$

Hướng dẫn:

Rút gọn các phân số về phân số tối giản để tìm các phân số bằng nhau.

Lời giải:

Có: $\frac{{ - 7}}{{42}} = \frac{{ - 1}}{6};\,\,\,\frac{{12}}{{18}} = \frac{2}{3};\,\,\,\frac{3}{{ - 18}} = \frac{{ - 1}}{6};\,\,\,\frac{{ - 9}}{{54}} = \frac{{ - 1}}{6};\,\,\,\frac{{ - 10}}{{ - 15}} = \frac{2}{3};\,\,\,\frac{{14}}{{20}} = \frac{7}{{10}}$ $\frac{{ - 7}}{{42}} = \frac{{ - 1}}{6};\,\,\,\frac{{12}}{{18}} = \frac{2}{3};\,\,\,\frac{3}{{ - 18}} = \frac{{ - 1}}{6};\,\,\,\frac{{ - 9}}{{54}} = \frac{{ - 1}}{6};\,\,\,\frac{{ - 10}}{{ - 15}} = \frac{2}{3};\,\,\,\frac{{14}}{{20}} = \frac{7}{{10}}$

Vậy phân số $\frac{14}{20}$ $\frac{14}{20}$ không bằng phân số nào trong các phân số còn lại.

Bài 22 trang 15 SGK Toán 6 tập 2

Điền số thích hợp vào ô trống:

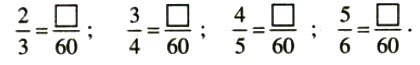
Giải Toán lớp 6 bài 4: Rút gọn phân số

Hướng dẫn:

Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.

Lời giải:

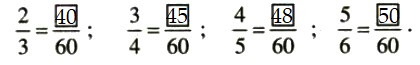
Bài 23 trang 16 SGK Toán 6 tập 2

Cho tập hợp A = {0;-3;5}. Viết tập hợp B các phân số $\frac{m}{n}$ $\frac{m}{n}$ mà m, n ∈ A. (Nếu có hai phân số bằng nhau thì chỉ cần viết một phân số).

Hướng dẫn:

Người ta gọi $\frac{a}{b}$ $\frac{a}{b}$ với a, b ∈ Z, b ≠ 0 là một phân số, a là tử số, b là mẫu số của phân số.

Lời giải:

Hướng dẫn giải

Vì 0 không thể là mẫu số nên các phân số phải tìm chỉ có thể có mẫu bằng - 3 hoặc 5.

Các phân số có mẫu số bằng -3 là: $\frac{0}{{ - 3}};\,\,\,\frac{{ - 3}}{{ - 3}};\,\,\,\frac{5}{{ - 3}}$ $\frac{0}{{ - 3}};\,\,\,\frac{{ - 3}}{{ - 3}};\,\,\,\frac{5}{{ - 3}}$

Các phân số có mẫu số bằng 5 là: $\frac{0}{5};\,\,\,\frac{{ - 3}}{5};\,\,\,\frac{5}{5}$ $\frac{0}{5};\,\,\,\frac{{ - 3}}{5};\,\,\,\frac{5}{5}$

Vì $\frac{0}{{ - 3}} = \frac{0}{5} = 0;\,\,\,\frac{{ - 3}}{{ - 3}} = \frac{5}{5} = 1$ $\frac{0}{{ - 3}} = \frac{0}{5} = 0;\,\,\,\frac{{ - 3}}{{ - 3}} = \frac{5}{5} = 1$

Vậy ta có tập hợp $B = \left\{ {\frac{{ - 5}}{3};\frac{{ - 3}}{5};0;1} \right\}$ $B = \left\{ {\frac{{ - 5}}{3};\frac{{ - 3}}{5};0;1} \right\}$

Bài 24 trang 16 SGK Toán 6 tập 2

Tìm các số nguyên x và y, biết:

$\frac{3}{x} = \frac{y}{{35}} = \frac{{ - 36}}{{84}}$ $\frac{3}{x} = \frac{y}{{35}} = \frac{{ - 36}}{{84}}$

Hướng dẫn:

Thực hiện rút gọn phân số $\frac{{ - 36}}{{84}}$ $\frac{{ - 36}}{{84}}$ để tìm x và y.

Lời giải:

Có $\frac{{ - 36}}{{84}} = \frac{{\left( { - 36} \right):\left( { - 12} \right)}}{{84:\left( { - 12} \right)}} = \frac{3}{{ - 7}}$ $\frac{{ - 36}}{{84}} = \frac{{\left( { - 36} \right):\left( { - 12} \right)}}{{84:\left( { - 12} \right)}} = \frac{3}{{ - 7}}$. Vậy x = - 7

Có $\frac{{ - 36}}{{84}} = \frac{3}{{ - 7}} = \frac{{3.\left( { - 5} \right)}}{{\left( { - 7} \right).\left( { - 5} \right)}} = \frac{{ - 15}}{{35}}$ $\frac{{ - 36}}{{84}} = \frac{3}{{ - 7}} = \frac{{3.\left( { - 5} \right)}}{{\left( { - 7} \right).\left( { - 5} \right)}} = \frac{{ - 15}}{{35}}$. Vậy y = -15

Bài 25 trang 16 SGK Toán 6 tập 2

Viết tất cả các phân số bằng $\frac{{15}}{{39}}$ $\frac{{15}}{{39}}$ mà tử và mẫu là các số tự nhiên có hai chữ số.

Hướng dẫn:

Rút gọn phân số $\frac{{15}}{{39}}$ $\frac{{15}}{{39}}$ về phân số tối giản.

Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.

Lời giải:

Có $\frac{{15}}{{39}} = \frac{{15:3}}{{39:3}} = \frac{5}{{13}}$ $\frac{{15}}{{39}} = \frac{{15:3}}{{39:3}} = \frac{5}{{13}}$

Ta có $\frac{5}{{13}} = \frac{{5.2}}{{13.2}} = \frac{{10}}{{26}};\,\,\,\frac{5}{{13}} = \frac{{5.4}}{{13.4}} = \frac{{20}}{{52}};\,\,\frac{5}{{13}} = \frac{{5.5}}{{13.5}} = \frac{{25}}{{65}}$ $\frac{5}{{13}} = \frac{{5.2}}{{13.2}} = \frac{{10}}{{26}};\,\,\,\frac{5}{{13}} = \frac{{5.4}}{{13.4}} = \frac{{20}}{{52}};\,\,\frac{5}{{13}} = \frac{{5.5}}{{13.5}} = \frac{{25}}{{65}}$

$\frac{5}{{13}} = \frac{{5.6}}{{13.6}} = \frac{{30}}{{78}};\,\,\,\frac{5}{{13}} = \frac{{5.7}}{{13.7}} = \frac{{35}}{{91}}$ $\frac{5}{{13}} = \frac{{5.6}}{{13.6}} = \frac{{30}}{{78}};\,\,\,\frac{5}{{13}} = \frac{{5.7}}{{13.7}} = \frac{{35}}{{91}}$

Vậy các phân số thỏa mãn yêu cầu đề bài là: $\frac{5}{{13}};\,\,\,\frac{{10}}{{26}};\,\,\,\frac{{15}}{{39}};\,\,\,\frac{{20}}{{52}};\,\,\,\frac{{25}}{{65}};\,\,\,\frac{{30}}{{78}};\,\,\,\frac{{35}}{{91}}$ $\frac{5}{{13}};\,\,\,\frac{{10}}{{26}};\,\,\,\frac{{15}}{{39}};\,\,\,\frac{{20}}{{52}};\,\,\,\frac{{25}}{{65}};\,\,\,\frac{{30}}{{78}};\,\,\,\frac{{35}}{{91}}$

Bài 26 trang 16 SGK Toán 6 tập 2

Cho đoạn thẳng AB:

Giải Toán lớp 6 bài 4: Rút gọn phân số

Hãy vẽ vào vở các đoạn thẳng CD, EF, GH, IK biết rằng:

CD = $\frac{3}{4}$ $\frac{3}{4}$AB; EF = $\frac{5}{6}$ $\frac{5}{6}$AB; GH = $\frac{1}{2}$ $\frac{1}{2}$AB; IK = $\frac{5}{4}$ $\frac{5}{4}$AB

Hướng dẫn:

Đoạn AB được chia thành 12 đoạn nhỏ bằng nhau. Do đó CD = $\frac{3}{4}$ $\frac{3}{4}$AB = $\frac{9}{{12}}$ $\frac{9}{{12}}$AB

Vậy: CD bằng 9 đoạn nhỏ, EF bằng 10 đoạn nhỏ, GH bằng 6 đoạn nhỏ, IK bằng 15 đoạn nhỏ.

Lời giải:

Bài 27 trang 16 SGK Toán 6 tập 2

Đố: Một học sinh đã " rút gọn" như sau:

$\frac{{10 + 5}}{{10 + 10}} = \frac{5}{{10}} = \frac{1}{2}$ $\frac{{10 + 5}}{{10 + 10}} = \frac{5}{{10}} = \frac{1}{2}$

Bạn đó giải thích: "Trước hết em rút gọn cho 10, rồi rút gọn cho 5". Đố em làm như vậy đúng hay sai? Vì sao?

Hướng dẫn giải

Theo quy tắc rút gọn, ta phải chia cả tử và mẫu của phân số cho cùng một số khác 0, nhưng học sinh này đã trừ cả tử và mẫu cho 10 nên bạn làm như vậy không đúng.

Chia sẻ, đánh giá bài viết

70

13.878

Bài trước

Bài sau

Chia sẻ bởi:
Nguyễn Thị Phương
Nhóm:
Sưu tầm
Ngày: 23/02/2021

Tải về

Chọn file muốn tải về: