Giải Toán lớp 6 bài 8: Tính chất cơ bản của phép cộng phân số

Giải bài tập môn Toán lớp 6

Giải bài tập trang 29, 30, 31 SGK Toán lớp 6 tập 2: Tính chất cơ bản của phép cộng phân số

A. Lý thuyết tính chất cơ bản của phép cộng phân số
B. Giải bài tập SGK Toán lớp 6 tập 2 trang 28, 29, 30, 31

Giải bài tập trang 28, 29, 30, 31 SGK Toán lớp 6 tập 2: Tính chất cơ bản của phép cộng phân số với các gợi ý đáp án và cách giải bài tập trong SGK sẽ giúp các em ghi nhớ và khắc sâu nội dung chính của bài học để vận dụng vào việc giải bài tập. Mời các em tham khảo tài liệu để dễ dàng hoàn thiện bài tập và sưu tầm thêm cho mình những phương pháp giải bài tập nhanh, chính xác.

A. Lý thuyết tính chất cơ bản của phép cộng phân số

Các tính chất: Tương tự như phép cộng số nguyên, phép cộng phân số có các tính chất cơ bản sau đây:

a) Tính chất giao hoán: $\frac{a}{b} + \frac{c}{d} = \frac{c}{d} + \frac{a}{b}$ $\frac{a}{b} + \frac{c}{d} = \frac{c}{d} + \frac{a}{b}$

b) Tính chất kết hợp: $\left( {\frac{a}{b} + \frac{c}{d}} \right) + \frac{p}{q} = \frac{a}{b} + \left( {\frac{c}{d} + \frac{p}{q}} \right)$ $\left( {\frac{a}{b} + \frac{c}{d}} \right) + \frac{p}{q} = \frac{a}{b} + \left( {\frac{c}{d} + \frac{p}{q}} \right)$

c) Cộng với số 0: $\frac{a}{b} + 0 = 0 + \frac{a}{b} = \frac{a}{b}$ $\frac{a}{b} + 0 = 0 + \frac{a}{b} = \frac{a}{b}$

B. Giải bài tập SGK Toán lớp 6 tập 2 trang 28, 29, 30, 31

Bài 47 trang 28 SGK Toán 6 tập 2

Tính nhanh:

a) $\frac{{ - 3}}{7} + \frac{5}{{13}} + \frac{{ - 4}}{7};$ $\frac{{ - 3}}{7} + \frac{5}{{13}} + \frac{{ - 4}}{7};$

b) $\frac{{ - 5}}{{21}} + \frac{{ - 2}}{{21}} + \frac{8}{{24}}$ $\frac{{ - 5}}{{21}} + \frac{{ - 2}}{{21}} + \frac{8}{{24}}$

Hướng dẫn:

Sử dụng tính chất giao hoán và kết hợp của phân số để tính nhanh.

Lời giải:

a) $\frac{{ - 3}}{7} + \frac{5}{{13}} + \frac{{ - 4}}{7} = \left( {\frac{{ - 3}}{7} + \frac{{ - 4}}{7}} \right) + \frac{5}{{13}} = - 1 + \frac{5}{{13}} = \frac{{ - 13}}{{13}} + \frac{5}{{13}} = \frac{{ - 8}}{{13}}$ $\frac{{ - 3}}{7} + \frac{5}{{13}} + \frac{{ - 4}}{7} = \left( {\frac{{ - 3}}{7} + \frac{{ - 4}}{7}} \right) + \frac{5}{{13}} = - 1 + \frac{5}{{13}} = \frac{{ - 13}}{{13}} + \frac{5}{{13}} = \frac{{ - 8}}{{13}}$

b) $\frac{{ - 5}}{{21}} + \frac{{ - 2}}{{21}} + \frac{8}{{24}} = \left( {\frac{{ - 5}}{{21}} + \frac{{ - 2}}{{21}}} \right) + \frac{1}{3} = \frac{{ - 7}}{{21}} + \frac{1}{3} = \frac{{ - 1}}{3} + \frac{1}{3} = \frac{0}{3} = 0$ $\frac{{ - 5}}{{21}} + \frac{{ - 2}}{{21}} + \frac{8}{{24}} = \left( {\frac{{ - 5}}{{21}} + \frac{{ - 2}}{{21}}} \right) + \frac{1}{3} = \frac{{ - 7}}{{21}} + \frac{1}{3} = \frac{{ - 1}}{3} + \frac{1}{3} = \frac{0}{3} = 0$

Bài 48 trang 28 SGK Toán 6 tập 2

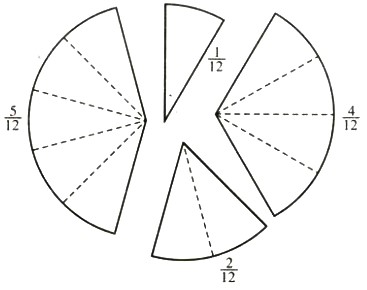
Đố: Cắt một tấm bìa hình tròn bán kính 2,5cm thành 4 phần không bằng nhau như hình 8. Đố em đặt các miếng bìa đã cắt cạnh nhau để được:

a) $\frac{1}{4}$ $\frac{1}{4}$ hình tròn;

b) $\frac{1}{2}$ $\frac{1}{2}$ hình tròn;

c) $\frac{7}{{12}},\,\,\,\frac{2}{3},\,\,\,\,\frac{3}{4},\,\,\,\frac{5}{6},\,\,\,\frac{{11}}{{12}}$ $\frac{7}{{12}},\,\,\,\frac{2}{3},\,\,\,\,\frac{3}{4},\,\,\,\frac{5}{6},\,\,\,\frac{{11}}{{12}}$ và $\frac{{12}}{{12}}$ $\frac{{12}}{{12}}$ hình tròn.

Giải bài tập trang 29, 30, 31 SGK Toán lớp 6 tập 2

Hình 8

Hướng dẫn:

Tách các phân số thành tổng của các phân số có mẫu số bằng 12: $\frac{1}{{12}},\,\,\frac{5}{{12}},\,\,\,\frac{4}{{12}},\,\,\,\frac{2}{{12}}$ $\frac{1}{{12}},\,\,\frac{5}{{12}},\,\,\,\frac{4}{{12}},\,\,\,\frac{2}{{12}}$.

Lời giải:

a) Có $\frac{1}{4} = \frac{3}{{12}} = \frac{1}{{12}} + \frac{2}{{12}}$ $\frac{1}{4} = \frac{3}{{12}} = \frac{1}{{12}} + \frac{2}{{12}}$ → Ghép hai tấm $\frac{1}{{12}},\,\frac{2}{{12}}$ $\frac{1}{{12}},\,\frac{2}{{12}}$ cạnh nhau.

b) Có $\frac{1}{2} = \frac{6}{{12}} = \frac{5}{{12}} + \frac{1}{{12}}$ $\frac{1}{2} = \frac{6}{{12}} = \frac{5}{{12}} + \frac{1}{{12}}$ → Ghép hai tấm $\frac{1}{{12}},\,\frac{5}{{12}}$ $\frac{1}{{12}},\,\frac{5}{{12}}$ cạnh nhau.

c) Có $\frac{7}{{12}} = \frac{5}{{12}} + \frac{2}{{12}}$ $\frac{7}{{12}} = \frac{5}{{12}} + \frac{2}{{12}}$ → Ghép hai tấm $\frac{2}{{12}},\,\frac{5}{{12}}$ $\frac{2}{{12}},\,\frac{5}{{12}}$ cạnh nhau.

$\frac{2}{3} = \frac{8}{{12}} = \frac{4}{{12}} + \frac{4}{{12}}$ $\frac{2}{3} = \frac{8}{{12}} = \frac{4}{{12}} + \frac{4}{{12}}$ → Ghép hai tấm $\frac{4}{{12}},\,\frac{4}{{12}}$ $\frac{4}{{12}},\,\frac{4}{{12}}$ cạnh nhau.

$\frac{3}{4} = \frac{9}{{12}} = \frac{5}{{12}} + \frac{4}{{12}}$ $\frac{3}{4} = \frac{9}{{12}} = \frac{5}{{12}} + \frac{4}{{12}}$ → Ghép hai tấm $\frac{4}{{12}},\,\frac{5}{{12}}$ $\frac{4}{{12}},\,\frac{5}{{12}}$ cạnh nhau.

$\frac{5}{6} = \frac{{10}}{{12}} = \frac{5}{{12}} + \frac{5}{{12}}$ $\frac{5}{6} = \frac{{10}}{{12}} = \frac{5}{{12}} + \frac{5}{{12}}$→ Ghép hai tấm $\frac{5}{{12}},\,\frac{5}{{12}}$ $\frac{5}{{12}},\,\frac{5}{{12}}$ cạnh nhau.

$\frac{{11}}{{12}} = \frac{5}{{12}} + \frac{5}{{12}} + \frac{1}{{12}}$ $\frac{{11}}{{12}} = \frac{5}{{12}} + \frac{5}{{12}} + \frac{1}{{12}}$→ Ghép ba tấm $\frac{1}{{12}},\,\frac{5}{{12}},\,\frac{5}{{12}}$ $\frac{1}{{12}},\,\frac{5}{{12}},\,\frac{5}{{12}}$ cạnh nhau.

$\frac{{12}}{{12}} = \frac{5}{{12}} + \frac{5}{{12}} + \frac{2}{{12}}$ $\frac{{12}}{{12}} = \frac{5}{{12}} + \frac{5}{{12}} + \frac{2}{{12}}$→ Ghép ba tấm $\frac{2}{{12}},\,\frac{5}{{12}},\,\frac{5}{{12}}$ $\frac{2}{{12}},\,\frac{5}{{12}},\,\frac{5}{{12}}$ cạnh nhau.

Bài 49 trang 29 SGK Toán 6 tập 2

Hùng đi xe đạp, 10 phút đầu đi được $\frac{1}{3}$ $\frac{1}{3}$ quãng đường, 10 phút thứ hai đi được $\frac{1}{4}$ $\frac{1}{4}$ quãng đường, 10 phút cuối cùng đi được $\frac{2}{9}$ $\frac{2}{9}$ quãng đường. Hỏi sau 30 phút Hùng đi được bao nhiêu phần quãng đường?

Hướng dẫn:

Số phần quãng đường Hùng đi bằng tổng các quãng đường mà Hùng đí được mỗi 10 phút.

Lời giải:

Sau 30 phút Hùng đi được quãng đường là: $\frac{1}{3} + \frac{1}{4} + \frac{2}{9} = \frac{{29}}{{36}}$ $\frac{1}{3} + \frac{1}{4} + \frac{2}{9} = \frac{{29}}{{36}}$ (quãng đường).

Bài 50 trang 29 SGK Toán 6 tập 2

Điền số thích hợp vào ô trống ở bảng dưới:

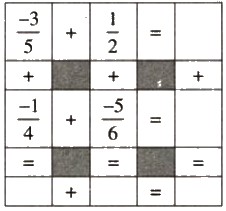
Giải bài tập trang 29, 30, 31 SGK Toán lớp 6 tập 2

Hướng dẫn:

Thực hiện phép cộng phân số để hoàn thành bảng.

Lời giải:

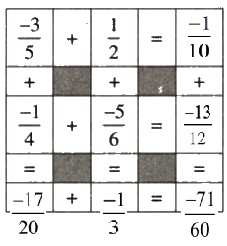
Bài 51 trang 29 SGK Toán 6 tập 2

Tìm năm cách chọn ba trong bảy số sau đây để khi cộng lại được tổng là 0:

$\frac{{ - 1}}{6},\,\,\,\frac{{ - 1}}{3},\,\,\,\frac{{ - 1}}{2},\,\,\,0,\,\,\,\frac{1}{2},\,\,\,\frac{1}{3},\,\,\,\frac{1}{6}$ $\frac{{ - 1}}{6},\,\,\,\frac{{ - 1}}{3},\,\,\,\frac{{ - 1}}{2},\,\,\,0,\,\,\,\frac{1}{2},\,\,\,\frac{1}{3},\,\,\,\frac{1}{6}$

Ví dụ: $\frac{{ - 1}}{2} + \frac{1}{3} + \frac{1}{6} = 0$ $\frac{{ - 1}}{2} + \frac{1}{3} + \frac{1}{6} = 0$

Hướng dẫn:

Các số đối nhau có tổng bằng 0.

Lựa chọn hai phân số có tổng là số đối của phân số thứ ba, khi đó tổng của ba số sẽ bằng 0.

Lời giải:

Cách 1: $\frac{{ - 1}}{2} + \frac{1}{3} + \frac{1}{6} =0$ $\frac{{ - 1}}{2} + \frac{1}{3} + \frac{1}{6} =0$

Cách 2: $\frac{1}{2} + \frac{{ - 1}}{3} + \frac{{ - 1}}{6} = 0$ $\frac{1}{2} + \frac{{ - 1}}{3} + \frac{{ - 1}}{6} = 0$

Cách 3: $\frac{1}{2} + \frac{{ - 1}}{2} + 0 = 0$ $\frac{1}{2} + \frac{{ - 1}}{2} + 0 = 0$

Cách 4: $\frac{1}{3} + \frac{{ - 1}}{3} + 0 = 0$ $\frac{1}{3} + \frac{{ - 1}}{3} + 0 = 0$

Cách 5: $\frac{1}{6} + \frac{{ - 1}}{6} + 0 = 0$ $\frac{1}{6} + \frac{{ - 1}}{6} + 0 = 0$

Bài 52 trang 29 SGK Toán 6 tập 2

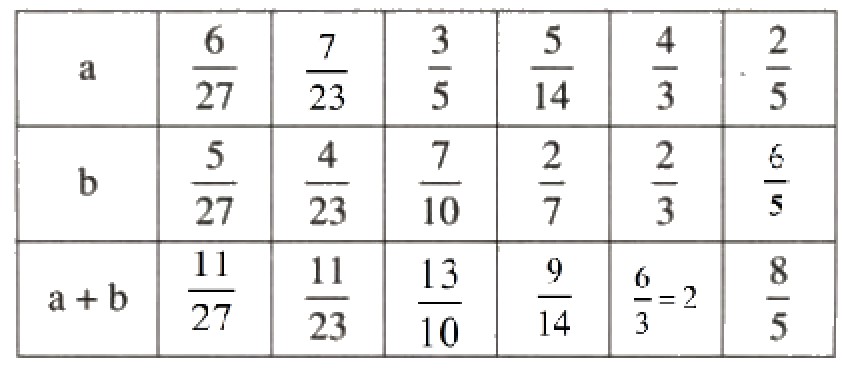
Điền số thích hợp vào ô trống:

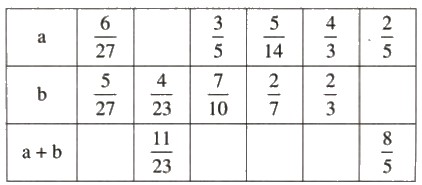
Giải bài tập trang 29, 30, 31 SGK Toán lớp 6 tập 2

Hướng dẫn:

Sử dụng phép cộng hai phân số để điền các số thích hợp vào ô trống.

Lời giải:

Giải bài tập trang 29, 30, 31 SGK Toán lớp 6 tập 2

Bài 53 trang 30 SGK Toán 6 tập 2

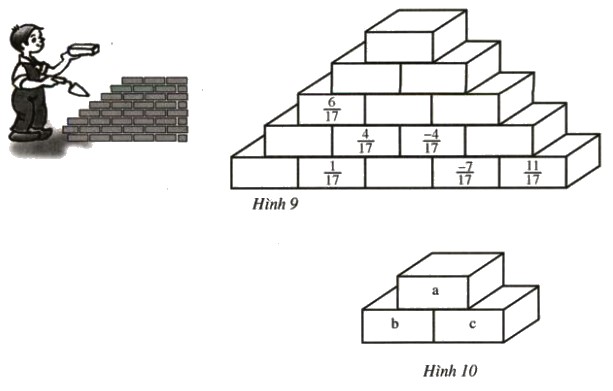
"Xây tường".

Em hãy "xây bức tường" ở hình 9 này bằng các điền các phân số thích hợp vào các viên gạch theo quy tắc sau:

a = b + c (h.10)

Giải bài tập trang 29, 30, 31 SGK Toán lớp 6 tập 2

Hướng dẫn:

Sử dụng phép cộng hai phân số để điền các số thích hợp vào ô trống.

Lời giải:

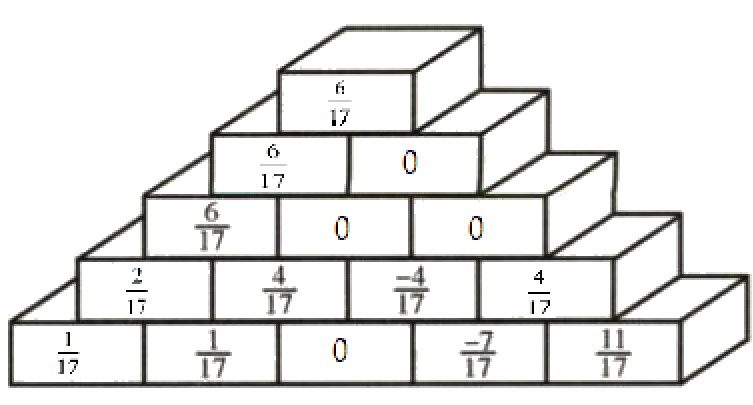
Giải bài tập trang 29, 30, 31 SGK Toán lớp 6 tập 2

Bài 54 trang 30 SGK Toán 6 tập 2

Trong vở bài tập của bạn An có bài làm sau:

a) $\frac{{ - 3}}{5} + \frac{1}{5} = \frac{4}{5}$ $\frac{{ - 3}}{5} + \frac{1}{5} = \frac{4}{5}$

b) $\frac{{ - 10}}{{13}} + \frac{{ - 2}}{{13}} = \frac{{ - 12}}{{13}}$ $\frac{{ - 10}}{{13}} + \frac{{ - 2}}{{13}} = \frac{{ - 12}}{{13}}$

c) $\frac{2}{3} + \frac{{ - 1}}{6} = \frac{4}{6} + \frac{{ - 1}}{6} = \frac{3}{6} = \frac{1}{2}$ $\frac{2}{3} + \frac{{ - 1}}{6} = \frac{4}{6} + \frac{{ - 1}}{6} = \frac{3}{6} = \frac{1}{2}$

d) $\frac{{ - 2}}{3} + \frac{2}{{ - 5}} = \frac{{ - 2}}{3} + \frac{{ - 2}}{5} = \frac{{ - 10}}{{15}} + \frac{{ - 6}}{{15}} = \frac{{ - 4}}{{15}}$ $\frac{{ - 2}}{3} + \frac{2}{{ - 5}} = \frac{{ - 2}}{3} + \frac{{ - 2}}{5} = \frac{{ - 10}}{{15}} + \frac{{ - 6}}{{15}} = \frac{{ - 4}}{{15}}$

Hãy kiểm tra lại các đáp số và sửa lại chỗ sai (nếu có).

Hướng dẫn:

Bạn An làm sai ở quy tắc cộng hai số nguyên cùng dấu và cộng hai số nguyên khác dấu khi cộng các tử số của phân số có cùng mẫu số.

Lời giải:

a) $\frac{{ - 3}}{5} + \frac{1}{5} = \frac{-2}{5}$ $\frac{{ - 3}}{5} + \frac{1}{5} = \frac{-2}{5}$

b) Bài làm đúng.

c) Bài làm đúng.

d) $\frac{{ - 2}}{3} + \frac{2}{{ - 5}} = \frac{{ - 2}}{3} + \frac{{ - 2}}{5} = \frac{{ - 10}}{{15}} + \frac{{ - 6}}{{15}} = \frac{{ - 16}}{{15}}$ $\frac{{ - 2}}{3} + \frac{2}{{ - 5}} = \frac{{ - 2}}{3} + \frac{{ - 2}}{5} = \frac{{ - 10}}{{15}} + \frac{{ - 6}}{{15}} = \frac{{ - 16}}{{15}}$

Bài 55 trang 30 SGK Toán 6 tập 2

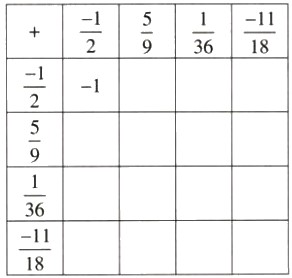
Điền số thích hợp vào ô trống. Chú ý rút gọn kết quả (nếu có thể):

Giải bài tập trang 29, 30, 31 SGK Toán lớp 6 tập 2

Hướng dẫn:

Sử dụng phép cộng hai phân số để điền các số thích hợp vào ô trống.

Lời giải:

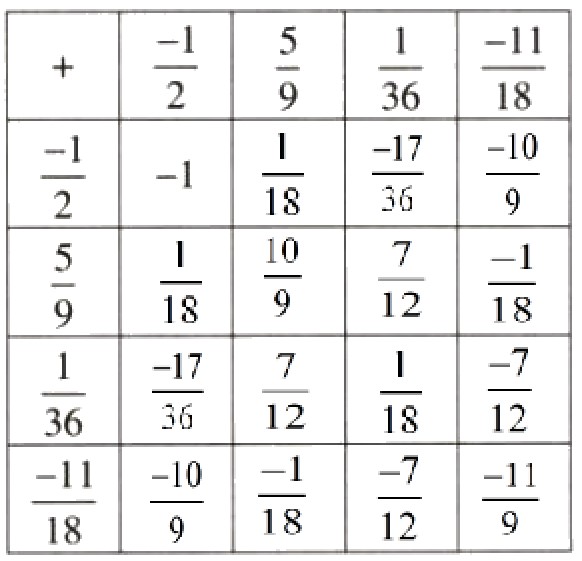
Giải bài tập trang 29, 30, 31 SGK Toán lớp 6 tập 2

Bài 56 trang 31 SGK Toán 6 tập 2

Tính nhanh giá trị của các biểu thức sau:

$\begin{array}{l} A = \frac{{ - 5}}{{11}} + \left( {\frac{{ - 6}}{{11}} + 1} \right)\\ B = \frac{2}{3} + \left( {\frac{5}{7} + \frac{{ - 2}}{3}} \right)\\ C = \left( {\frac{{ - 1}}{4} + \frac{5}{8}} \right) + \frac{{ - 3}}{8} \end{array}$ $\begin{array}{l} A = \frac{{ - 5}}{{11}} + \left( {\frac{{ - 6}}{{11}} + 1} \right)\\ B = \frac{2}{3} + \left( {\frac{5}{7} + \frac{{ - 2}}{3}} \right)\\ C = \left( {\frac{{ - 1}}{4} + \frac{5}{8}} \right) + \frac{{ - 3}}{8} \end{array}$

Hướng dẫn:

Sử dụng tính chất kết hợp, giao hoán và cộng với số 0 để tính nhanh các giá trị của biểu thức.

Hai số đối nhau có tổng bằng 0.

Lời giải:

$A = \frac{{ - 5}}{{11}} + \left( {\frac{{ - 6}}{{11}} + 1} \right) = \left( {\frac{{ - 5}}{{11}} + \frac{{ - 6}}{{11}}} \right) + 1 = \frac{{ - 11}}{{11}} + 1 = \left( { - 1} \right) + 1 = 0$ $A = \frac{{ - 5}}{{11}} + \left( {\frac{{ - 6}}{{11}} + 1} \right) = \left( {\frac{{ - 5}}{{11}} + \frac{{ - 6}}{{11}}} \right) + 1 = \frac{{ - 11}}{{11}} + 1 = \left( { - 1} \right) + 1 = 0$

$B = \frac{2}{3} + \left( {\frac{5}{7} + \frac{{ - 2}}{3}} \right) = \left( {\frac{2}{3} + \frac{{ - 2}}{3}} \right) + \frac{5}{7} = 0 + \frac{5}{7} = \frac{5}{7}$ $B = \frac{2}{3} + \left( {\frac{5}{7} + \frac{{ - 2}}{3}} \right) = \left( {\frac{2}{3} + \frac{{ - 2}}{3}} \right) + \frac{5}{7} = 0 + \frac{5}{7} = \frac{5}{7}$

$C = \left( {\frac{{ - 1}}{4} + \frac{5}{8}} \right) + \frac{{ - 3}}{8} = \frac{{ - 1}}{4} + \left( {\frac{5}{8} + \frac{{ - 3}}{8}} \right) = \frac{{ - 1}}{4} + \frac{2}{8} = \frac{{ - 1}}{4} + \frac{1}{4} = 0$ $C = \left( {\frac{{ - 1}}{4} + \frac{5}{8}} \right) + \frac{{ - 3}}{8} = \frac{{ - 1}}{4} + \left( {\frac{5}{8} + \frac{{ - 3}}{8}} \right) = \frac{{ - 1}}{4} + \frac{2}{8} = \frac{{ - 1}}{4} + \frac{1}{4} = 0$

Bài 57 trang 28 SGK Toán 6 tập 2

Trong các câu sau đây, hãy chọn một câu đúng:

Muốn cộng hai phân số $\frac{{ - 3}}{4}$ $\frac{{ - 3}}{4}$ và $\frac{4}{5}$ $\frac{4}{5}$ ta làm như sau:

a) Cộng tử với tử, cộng mẫu với mẫu.

b) Nhân mẫu số của phân số $\frac{{ - 3}}{4}$ $\frac{{ - 3}}{4}$ với 5, nhân mẫu của phân số $\frac{{ 4}}{5}$ $\frac{{ 4}}{5}$ với 4 rồi cộng hai tử lại.

c) Nhân cả tử lẫn mẫu của phân số $\frac{{ - 3}}{4}$ $\frac{{ - 3}}{4}$ với 5, nhân cả tử lẫn mẫu của phân số $\frac{{ 4}}{5}$ $\frac{{ 4}}{5}$ với 4 rồi cộng hai tử mới lại, giữ nguyên mẫu chung.

d) Nhân cả tử lẫn mẫu của phân số $\frac{-3}{4}$ $\frac{-3}{4}$ với 5, nhân cả tử lẫn mẫu của phân số $\frac{4}{5}$ $\frac{4}{5}$ với 4 rồi cộng tử với tử, mẫu với mẫu

Hướng dẫn:

Học sinh nhớ lại quy tắc cộng hai phân số có cùng mẫu số và cộng hai phân số khác mẫu số để tìm được đáp án đúng.

Lời giải:

Đáp án đúng là đáp án c)

Chia sẻ, đánh giá bài viết

61

7.631

Bài trước

Bài sau