Giải Toán lớp 6 bài 5: Quy đồng mẫu số nhiều phân số

Giải bài tập môn Toán lớp 6

Giải bài tập trang 19, 20 SGK Toán lớp 6 tập 2: Quy đồng mẫu số nhiều phân số

A. Lý thuyết quy đồng mẫu số nhiều phân số
- 1. Khái niệm
- 2. Quy tắc quy đồng mẫu số
B. Giải bài tập SGK Toán lớp 6 tập 2 trang 19, 20

Giải bài tập SGK Toán lớp 6 Đại số Chương 3 bài 5: Quy đồng mẫu số nhiều phân số sẽ giúp các em học sinh định hướng và gợi ý cách giải các bài tập trang 19, 20 môn Toán lớp 6 tập 2 nhằm giúp các em ôn tập và nắm vững hơn nội dung chính của bài học. Bên cạnh đó, việc tham khảo tài liệu còn giúp các em dễ dàng hoàn thiện bài tập của mình, nắm được cách giải để vận dụng vào giải các bài tập liên quan đến phân số.

A. Lý thuyết quy đồng mẫu số nhiều phân số

1. Khái niệm

Quy đồng mẫu số của nhiều phân số là biến đổi những phân số đó lần lượt thành những phân số bằng chúng nhưng có cùng mẫu số.

2. Quy tắc quy đồng mẫu số

Muốn quy đồng mẫu số nhiều phân số với mẫu số dương ta làm như sau:

+ Bước 1: Tìm bội chung của các mẫu (thường là BCNN) để làm mẫu chung.

+ Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).

+ Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

B. Giải bài tập SGK Toán lớp 6 tập 2 trang 19, 20

Bài 28 trang 19 SGK Toán 6 tập 2

a) Quy đồng mẫu các phân số sau: $\frac{{ - 3}}{{16}},\,\,\,\frac{5}{{24}},\,\,\,\frac{{ - 21}}{{56}}$ $\frac{{ - 3}}{{16}},\,\,\,\frac{5}{{24}},\,\,\,\frac{{ - 21}}{{56}}$.

b) Trong các phân số đã cho, phân số nào chưa tối giản?

Từ nhận xét đó, ta có thể quy đồng các phân số này như thế nào?

Hướng dẫn:

Thực hiện biến đổi các phân số đã cho thành các phân số tương ứng bằng chúng nhưng cùng có chung một mẫu số.

Lời giải:

a) BCNN (16, 24, 56) = 336 ➝ Mẫu số chung của các phân số là 336.

Quy đồng mẫu số các phân số được: $\frac{{ - 3}}{{16}} = \frac{{ - 63}}{{336}},\,\,\,\frac{5}{{24}} = \frac{{70}}{{336}},\,\,\,\frac{{ - 21}}{{56}} = \frac{{ - 126}}{{336}}$ $\frac{{ - 3}}{{16}} = \frac{{ - 63}}{{336}},\,\,\,\frac{5}{{24}} = \frac{{70}}{{336}},\,\,\,\frac{{ - 21}}{{56}} = \frac{{ - 126}}{{336}}$

b) Phân số $\frac{{ - 21}}{{56}}$ $\frac{{ - 21}}{{56}}$ không phải là phân số tối giản.

Từ đó ta có: Để quy đồng mẫu các phân số đã cho, trước hết ta nên rút gọn các phân số đã cho thành phân số tối giản rồi hãy quy đồng mẫu. Nếu làm như vậy ta sẽ được các phân số đơn giản hơn là $\frac{{ - 9}}{{48}},\,\,\,\frac{{10}}{{48}},\,\,\,\frac{{ - 18}}{{48}}$ $\frac{{ - 9}}{{48}},\,\,\,\frac{{10}}{{48}},\,\,\,\frac{{ - 18}}{{48}}$

Bài 29 trang 19 SGK Toán 6 tập 2

Quy đồng mẫu các phân số sau:

a) $\frac{3}{8}$ $\frac{3}{8}$ và $\frac{5}{27}$ $\frac{5}{27}$

b) $\frac{-2}{9}$ $\frac{-2}{9}$ và $\frac{4}{25}$ $\frac{4}{25}$

c) $\frac{1}{15}$ $\frac{1}{15}$ và - 6

Hướng dẫn:

Thực hiện biến đổi các phân số đã cho thành các phân số tương ứng bằng chúng nhưng cùng có chung một mẫu số.

Lời giải:

a) $\frac{3}{8} = \frac{{81}}{{216}}$ $\frac{3}{8} = \frac{{81}}{{216}}$ và $\frac{5}{27} = \frac{{40}}{{216}}$ $\frac{5}{27} = \frac{{40}}{{216}}$

b) $\frac{{ - 2}}{9} = \frac{{ - 50}}{{225}}$ $\frac{{ - 2}}{9} = \frac{{ - 50}}{{225}}$ và $\frac{4}{{25}} = \frac{{36}}{{225}}$ $\frac{4}{{25}} = \frac{{36}}{{225}}$

c) $\frac{1}{15}$ $\frac{1}{15}$ và $-6=\frac{-6}{1}=\frac{-90}{15}$ $-6=\frac{-6}{1}=\frac{-90}{15}$

Bài 30 trang 19 SGK Toán 6 tập 2

Quy đồng mẫu các phân số sau:

a) $\frac{{11}}{{120}}$ $\frac{{11}}{{120}}$ và $\frac{7}{{40}}$ $\frac{7}{{40}}$	b) $\frac{{24}}{{146}}$ $\frac{{24}}{{146}}$ và $\frac{{6}}{{13}}$ $\frac{{6}}{{13}}$
c) $\frac{7}{{30}},\,\,\,\frac{{13}}{{60}},\,\,\,\frac{{ - 9}}{{40}}$ $\frac{7}{{30}},\,\,\,\frac{{13}}{{60}},\,\,\,\frac{{ - 9}}{{40}}$	d) $\frac{{17}}{{60}},\,\,\,\frac{{ - 5}}{{18}},\,\,\,\frac{{ - 64}}{{90}}$ $\frac{{17}}{{60}},\,\,\,\frac{{ - 5}}{{18}},\,\,\,\frac{{ - 64}}{{90}}$

Hướng dẫn:

Thực hiện biến đổi các phân số đã cho thành các phân số tương ứng bằng chúng nhưng cùng có chung một mẫu số.

Lời giải:

a) $\frac{{11}}{{120}}$ $\frac{{11}}{{120}}$ và $\frac{7}{{40}}$ $\frac{7}{{40}}$

b) Vì $\frac{{24}}{{146}} = \frac{{12}}{{73}}$ $\frac{{24}}{{146}} = \frac{{12}}{{73}}$ nên quy đồng mẫu số hai phân số ta được $\frac{{156}}{{949}}$ $\frac{{156}}{{949}}$ và $\frac{{438}}{{949}}$ $\frac{{438}}{{949}}$

c) $\frac{{28}}{{120}},\,\,\,\frac{{26}}{{120}},\,\,\,\frac{{ - 27}}{{120}}$ $\frac{{28}}{{120}},\,\,\,\frac{{26}}{{120}},\,\,\,\frac{{ - 27}}{{120}}$

d) $\frac{{51}}{{180}},\,\,\,\frac{{ - 50}}{{180}},\,\,\,\frac{{ - 128}}{{180}}$ $\frac{{51}}{{180}},\,\,\,\frac{{ - 50}}{{180}},\,\,\,\frac{{ - 128}}{{180}}$

Bài 31 trang 19 SGK Toán 6 tập 2

Hai phân số sau đây có bằng nhau không?

a) $\frac{{ - 5}}{{14}}$ $\frac{{ - 5}}{{14}}$ và $\frac{{30}}{{ - 84}}$ $\frac{{30}}{{ - 84}}$

b) $\frac{{ - 6}}{{102}}$ $\frac{{ - 6}}{{102}}$ và $\frac{{ - 9}}{{153}}$ $\frac{{ - 9}}{{153}}$

Hướng dẫn:

Rút gọn để được những phân số tối giản rồi so sánh.

a) Có, vì $\frac{{30}}{{ - 84}} = \frac{{ - 30}}{{84}} = \frac{{ - 5}}{{14}}$ $\frac{{30}}{{ - 84}} = \frac{{ - 30}}{{84}} = \frac{{ - 5}}{{14}}$

b) Có, vì $\frac{{ - 6}}{{102}} = \frac{{ - 1}}{{17}}$ $\frac{{ - 6}}{{102}} = \frac{{ - 1}}{{17}}$ và $\frac{{ - 9}}{{153}} = \frac{{ - 1}}{{17}}$ $\frac{{ - 9}}{{153}} = \frac{{ - 1}}{{17}}$

Bài 32 trang 19 SGK Toán 6 tập 2

Quy đồng mẫu các phân số:

a) $\frac{{ - 4}}{7},\,\,\,\frac{8}{9},\,\,\,\frac{{ - 10}}{{21}}$ $\frac{{ - 4}}{7},\,\,\,\frac{8}{9},\,\,\,\frac{{ - 10}}{{21}}$

b) $\frac{5}{{{2^2}.3}},\,\,\,\frac{7}{{{2^3}.11}}$ $\frac{5}{{{2^2}.3}},\,\,\,\frac{7}{{{2^3}.11}}$

Hướng dẫn:

Muốn quy đồng mẫu số nhiều phân số với mẫu số dương ta làm như sau:

+ Bước 1: Tìm bội chung của các mẫu (thường là BCNN) để làm mẫu chung.

+ Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).

+ Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

Lời giải:

a) Vì BCNN (7, 9, 21) = 63 nên mẫu số chung của các phân số là 63.

$\frac{{ - 4}}{7} = \frac{{ - 36}}{{63}},\,\,\,\frac{8}{9} = \frac{{56}}{{63}},\,\,\,\frac{{ - 10}}{{21}} = \frac{{ - 30}}{{63}}$ $\frac{{ - 4}}{7} = \frac{{ - 36}}{{63}},\,\,\,\frac{8}{9} = \frac{{56}}{{63}},\,\,\,\frac{{ - 10}}{{21}} = \frac{{ - 30}}{{63}}$

b) Vì BCNN (2².3, 2³.11) = 2³.3.11 = 264 nên mẫu số chung của các phân số là 264.

$\frac{5}{{{2^2}.3}} = \frac{5}{{12}} = \frac{{110}}{{264}},\,\,\,\frac{7}{{{2^3}.11}} = \frac{7}{{88}} = \frac{{21}}{{264}}$ $\frac{5}{{{2^2}.3}} = \frac{5}{{12}} = \frac{{110}}{{264}},\,\,\,\frac{7}{{{2^3}.11}} = \frac{7}{{88}} = \frac{{21}}{{264}}$

Bài 33 trang 19 SGK Toán 6 tập 2

a) $\frac{3}{{ - 20}},\,\,\,\frac{{ - 11}}{{ - 30}},\,\,\,\,\frac{7}{{15}}$ $\frac{3}{{ - 20}},\,\,\,\frac{{ - 11}}{{ - 30}},\,\,\,\,\frac{7}{{15}}$

b) $\frac{{ - 6}}{{ - 35}},\,\,\,\frac{{27}}{{ - 180}},\,\,\,\frac{{ - 3}}{{ - 28}}$ $\frac{{ - 6}}{{ - 35}},\,\,\,\frac{{27}}{{ - 180}},\,\,\,\frac{{ - 3}}{{ - 28}}$

Hướng dẫn:

Muốn quy đồng mẫu số nhiều phân số với mẫu số dương ta làm như sau:

+ Bước 1: Tìm bội chung của các mẫu (thường là BCNN) để làm mẫu chung.

+ Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).

+ Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

Lời giải:

a) Mẫu số chung của các phân số bằng 60.

$\frac{3}{{ - 20}} = \frac{{ - 3}}{{20}} = \frac{{ - 9}}{{60}},\,\,\,\frac{{ - 11}}{{ - 30}} = \frac{{11}}{{30}} = \frac{{22}}{{60}},\,\,\,\frac{7}{{15}} = \frac{{28}}{{60}}$ $\frac{3}{{ - 20}} = \frac{{ - 3}}{{20}} = \frac{{ - 9}}{{60}},\,\,\,\frac{{ - 11}}{{ - 30}} = \frac{{11}}{{30}} = \frac{{22}}{{60}},\,\,\,\frac{7}{{15}} = \frac{{28}}{{60}}$

b) Mẫu số chung của các phân số bằng 420.

$\frac{{ - 6}}{{ - 35}} = \frac{6}{{35}} = \frac{{72}}{{420}},\,\,\,\frac{{27}}{{ - 180}} = \frac{{ - 3}}{{20}} = \frac{{ - 63}}{{420}},\,\,\,\frac{{ - 3}}{{ - 28}} = \frac{3}{{28}} = \frac{{45}}{{420}}$ $\frac{{ - 6}}{{ - 35}} = \frac{6}{{35}} = \frac{{72}}{{420}},\,\,\,\frac{{27}}{{ - 180}} = \frac{{ - 3}}{{20}} = \frac{{ - 63}}{{420}},\,\,\,\frac{{ - 3}}{{ - 28}} = \frac{3}{{28}} = \frac{{45}}{{420}}$

Bài 34 trang 20 SGK Toán 6 tập 2

Quy đồng mẫu các phân số:

a) $\frac{{ - 5}}{5},\,\,\,\frac{8}{7}$ $\frac{{ - 5}}{5},\,\,\,\frac{8}{7}$

b) $3,\,\,\,\frac{{ - 3}}{5},\,\,\,\frac{{ - 5}}{6}$ $3,\,\,\,\frac{{ - 3}}{5},\,\,\,\frac{{ - 5}}{6}$

c) $\frac{{ - 9}}{7},\,\,\,\frac{{ - 19}}{{15}},\,\,\, - 1$ $\frac{{ - 9}}{7},\,\,\,\frac{{ - 19}}{{15}},\,\,\, - 1$

Hướng dẫn:

Thực hiện biến đổi các phân số đã cho thành các phân số tương ứng bằng chúng nhưng cùng có chung một mẫu số.

Lời giải:

a) $\frac{{ - 5}}{5} = - 1 = \frac{{ - 7}}{7},\,\,\,\frac{8}{7}$ $\frac{{ - 5}}{5} = - 1 = \frac{{ - 7}}{7},\,\,\,\frac{8}{7}$

b) $3 = \frac{3}{1} = \frac{{90}}{{30}},\,\,\,\frac{{ - 3}}{5} = \frac{{ - 18}}{{30}},\,\,\,\frac{{ - 5}}{6} = \frac{{ - 25}}{{30}}$ $3 = \frac{3}{1} = \frac{{90}}{{30}},\,\,\,\frac{{ - 3}}{5} = \frac{{ - 18}}{{30}},\,\,\,\frac{{ - 5}}{6} = \frac{{ - 25}}{{30}}$

c) $\frac{{ - 9}}{7} = \frac{{ - 135}}{{105}},\,\,\,\frac{{ - 19}}{{15}} = \frac{{ - 133}}{{105}},\,\,\, - 1 = \frac{{ - 105}}{{105}}$ $\frac{{ - 9}}{7} = \frac{{ - 135}}{{105}},\,\,\,\frac{{ - 19}}{{15}} = \frac{{ - 133}}{{105}},\,\,\, - 1 = \frac{{ - 105}}{{105}}$

Bài 35 trang 20 SGK Toán 6 tập 2

Rút gọn rồi quy đồng mẫu các phân số:

a) $\frac{{ - 15}}{{90}},\,\,\,\frac{{120}}{{600}},\,\,\,\frac{{ - 75}}{{150}}$ $\frac{{ - 15}}{{90}},\,\,\,\frac{{120}}{{600}},\,\,\,\frac{{ - 75}}{{150}}$

b) $\frac{{54}}{{ - 90}},\,\,\,\frac{{ - 180}}{{288}},\,\,\,\frac{{60}}{{ - 135}}$ $\frac{{54}}{{ - 90}},\,\,\,\frac{{ - 180}}{{288}},\,\,\,\frac{{60}}{{ - 135}}$

Hướng dẫn:

Thực hiện biến đổi các phân số đã cho thành các phân số tương ứng bằng chúng nhưng cùng có chung một mẫu số.

Lời giải:

a) $\frac{{ - 15}}{{90}} = \frac{{ - 1}}{6} = \frac{{ - 5}}{{30}}$ $\frac{{ - 15}}{{90}} = \frac{{ - 1}}{6} = \frac{{ - 5}}{{30}}$

$\frac{{120}}{{600}} = \frac{1}{5} = \frac{6}{{30}}$ $\frac{{120}}{{600}} = \frac{1}{5} = \frac{6}{{30}}$

$\frac{{ - 75}}{{150}} = \frac{{ - 1}}{2} = \frac{{ - 15}}{{30}}$ $\frac{{ - 75}}{{150}} = \frac{{ - 1}}{2} = \frac{{ - 15}}{{30}}$

b) $\frac{{54}}{{ - 90}} = \frac{{ - 54}}{{90}} = \frac{{ - 3}}{5} = \frac{{ - 216}}{{360}}$ $\frac{{54}}{{ - 90}} = \frac{{ - 54}}{{90}} = \frac{{ - 3}}{5} = \frac{{ - 216}}{{360}}$

$\frac{{ - 180}}{{288}} = \frac{{ - 5}}{8} = \frac{{ - 225}}{{360}}$ $\frac{{ - 180}}{{288}} = \frac{{ - 5}}{8} = \frac{{ - 225}}{{360}}$

$\frac{{60}}{{ - 135}} = \frac{{ - 60}}{{135}} = \frac{{ - 4}}{9} = \frac{{ - 160}}{{360}}$ $\frac{{60}}{{ - 135}} = \frac{{ - 60}}{{135}} = \frac{{ - 4}}{9} = \frac{{ - 160}}{{360}}$

Bài 36 trang 20 SGK Toán 6 tập 2

Đố vui: Hai bức ảnh dưới đây chụp di tích nào?

Giải bài tập trang 19, 20 SGK Toán lớp 6 tập 2

Cho các dãy phân số sau:

Giải bài tập trang 19, 20 SGK Toán lớp 6 tập 2

Hãy quy đồng mẫu các phân số của từng dãy rồi đoán nhận phận số thứ tư của dãy đó; viết nó dưới dạng tối giản rồi viết chữ cái ở dãy đó vào ô tương ứng với phân số ấy ở hình 6. Khi đó, em sẽ biết được hai địa danh của Việt Nam được UNESCO công nhận là di sản văn hóa thế giới vào năm 1999.

Chẳng hạn, ở dãy đầu có ghi chữ N, quy đồng mẫu ta được $\frac{2}{{10}},\,\,\,\frac{3}{{10}},\,\,\,\frac{4}{{10}}$ $\frac{2}{{10}},\,\,\,\frac{3}{{10}},\,\,\,\frac{4}{{10}}$ nên phân số thứ tư là $\frac{5}{{10}}$ $\frac{5}{{10}}$. Nó có dạng tối giản $\frac{1}{{2}}$ $\frac{1}{{2}}$, do đó ta điền chữ N vào hai ô ứng với số 1/2 trên hình 6.

Giải bài tập trang 19, 20 SGK Toán lớp 6 tập 2

Hướng dẫn:

Ta phải viết tiếp vào dãy số như sau:

Giải bài tập trang 19, 20 SGK Toán lớp 6 tập 2

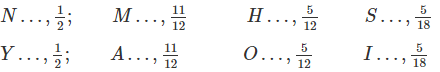
Ta có đáp án: HỘI AN; MỸ SƠN

Bài tiếp theo: Giải bài tập trang 23, 24 SGK Toán lớp 6 tập 2: So sánh phân số

Chia sẻ, đánh giá bài viết

97

23.962

Bài trước

Bài sau

Chia sẻ bởi:
Nguyễn Thị Phương
Nhóm:
Sưu tầm
Ngày: 18/03/2021

Tải về

Chọn file muốn tải về: