Toán lớp 6 bài 4
Toán 6 bài 4 của 3 bộ sách mới: Kết nối tri thức, Chân trời sáng tạo, Cánh Diều tổng hợp lời giải trong sách giáo khoa Toán lớp 6, giúp các em học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 6.
Toán lớp 6 bài 4
1. Giải Toán lớp 6 bài 4 sách Kết nối tri thức với cuộc sống
Toán lớp 6 bài 4 Phép cộng và phép trừ số tự nhiên Kết nối tri thức có lời giải bám sát chương trình học SGK. Toàn bộ đáp án chi tiết cho từng phần, từng bài tập trong nội dung chương trình học Toán 6 sách mới, giúp các em học sinh ôn tập, củng cố kiến thức, luyện tập Giải Toán 6 sách KNTT.
Toán lớp 6 tập 1 trang 16 Câu 1.17
Tính:
a) 63 548 + 19 256
b) 129 107 + 34 693
Đáp án
a) 63 548 + 19 256 = 82 804
b) 129 107 + 34 693 = 163 800
Toán lớp 6 tập 1 trang 16 Câu 1.18
Thay "?" bằng số thích hợp:
? + 2 895 = 2 895 + 6 789
Đáp án
Áp dụng tính chất giao hoán của phép cộng ta có:
? + 2 895 = 2 895 + 6 789. Suy ra "?" có giá trị 6 789
Toán lớp 6 tập 1 trang 16 Câu 1.19
Tìm số tự nhiên x thỏa mãn:
a) 7 + x = 362
b) 25 - x = 15
c) x - 56 = 4
Đáp án
a) 7 + x = 362
⇔ x = 362 - 7
⇔ x = 355
b) 25 - x = 15
⇔ x = 25 - 15
⇔ x = 10
c) x - 56 = 4
⇔ x = 56 + 4
⇔ x = 60
Toán lớp 6 tập 1 trang 16 Câu 1.20
Dân số Việt Nam năm 2019 là 96 462 106 người. Năm 2020, dân số Việt Nam tăng 876 473 người so với năm 2019. Tính dân số Việt Nam năm 2020. (Theo danso.org)
Đáp án
Dân số Việt Nam năm 2020 là:
96 462 106 + 876 473 = 97 338 579 (người)
Đáp số: 97 338 579 người
Toán lớp 6 tập 1 trang 16 Câu 1.21
Nhà ga số 1 và nhà ga số 2 của một sân bay có thể tiếp nhận tương ứng khoảng 6 526 300 và 3 514 500 lượt hành khách mỗi năm. Nhờ đưa vào sử dụng nhà ga số 3 mà mỗi năm sân bay này có thể tiếp nhận được khoảng 22 851 200 lượt hành khách. Hãy tính số lượt hành khách mà nhà ga số 3 có thể tiếp nhận mỗi năm.
Đáp án
Tổng số lượt hành khách mà nhà ga số 1 và số 2 có thể tiếp nhận mỗi năm là:
6 526 300 + 3 514 500 = 10 040 800 (lượt)
Số lượt hành khách mà nhà ga số 3 có thể tiếp nhận mỗi năm là:
22 851 200 - 10 040 800 = 12 810 400 (lượt)
Đáp số: 12 810 400 lượt hành khách
Toán lớp 6 tập 1 trang 16 Câu 1.22
Tính một cách hợp lí:
a) 285 + 470 + 115 + 230
b) 571 + 216 + 129 + 124
Đáp án
a) 285 + 470 + 115 + 230
= (285 + 115) + (470 + 230)
= 400 + 700
= 1 100
b) 571 + 216 + 129 + 124
= (571 + 129) + (216 + 124)
= 700 + 340
= 1 040
Trắc nghiệm Toán 6 bài 4 KNTT
Tham khảo chi tiết: Giải Toán lớp 6 bài 4 Phép cộng và phép trừ số tự nhiên Kết nối tri thức
2. Giải Toán lớp 6 bài 4 sách Chân trời sáng tạo
Toán lớp 6 bài 4 Lũy thừa với số mũ tự nhiên CTST bao gồm đáp án chi tiết cho từng phần, từng bài tập trong nội dung chương trình học bài 4 Toán 6 trang 16, 17, 18 giúp các em học sinh ôn tập, củng cố kiến thức, luyện tập Giải Toán 6 sách Chân trời sáng tạo.
Toán lớp 6 tập 1 trang 18 Câu 1
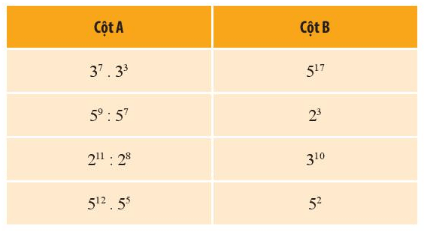
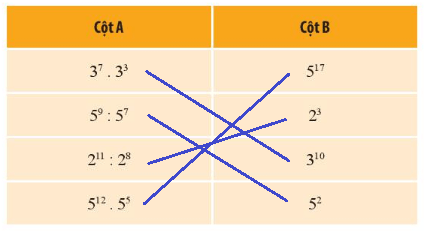
Ghép mỗi phép tính ở cột A với lũy thừa tương ứng của nó ở cột B.
Đáp án
Toán lớp 6 tập 1 trang 18 Câu 2
a) Viết kết quả của mỗi phép tính sau dưới dạng một lũy thừa:
5 7 : 5 5 ; 9 5 : 8 0 ; 2 10 : 64 . 16.
b) Viết cấu tạo thập phân của các số 4 983, 54 297, 2 023 theo mẫu sau:
4 983 = 4 . 1000 + 9 . 100 + 8 . 10 + 3
= 4 . 10 3 + 9 . 10 2 + 8 . 10 + 3
Đáp án
a) 57 : 55 = 57 − 2 = 55 .
95 : 80 = 95 : 1 = 95 .
210 : 64 . 16 = 210 : 26 . 24 = 210 – 6 + 4 = 28 .
b) 54 297 = 5 . 10000 + 4 . 1000 + 2 . 100 + 9 . 10 + 7
= 5 . 10 3 = 4 . 103 + 2 . 102 + 9 . 10 + 7
2 023 = 2 . 1000 + 0. 100 + 2 . 10 + 3
= 2 . 103 + 2 . 10 + 3
Toán lớp 6 tập 1 trang 18 Câu 3
Theo Tổng cục Thống kê, tháng 10 năm 2020 dân số Việt Nam được làm tròn là 98 000 000 người. Em hãy viết dân số của Việt Nam dưới dạng tích của một số với một lũy thừa của 10.
Đáp án
Viết dân số của Việt Nam dưới dạng tích của một số với một lũy thừa của 10 như sau:
98 000 000 = 98 . 106
Toán lớp 6 tập 1 trang 18 Câu 4
Biết rằng khối lượng của Trái Đất khoảng 6 00 … 000 (21 số 0) tấn, khối lượng của Mặt Trăng khoảng 75 00 … 000 (18 số 0) tấn.
a) Em hãy viết khối lượng của Trái Đất và khối lượng của Mặt Trăng dưới dạng tích của một số với một tích của một số với một lũy thừa của 10.
b) Khối lượng Trái Đất gấp bao nhiêu lần khối lượng Mặt Trăng?
Đáp án
a) Khối lượng của Trái Đất = 6 . 1021 tấn
Khối lượng của Mặt Trăng = 75 . 1018 tấn
b) Khối lượng Trái Đất gấp khối lượng Mặt Trăng:
![]() \(\left(6 \cdot 10^{21}\right):\left(75 \cdot 10^{18}\right)=\frac{6}{75} \cdot 10^{21-18}=\frac{6}{75} \cdot 10^{3}\)
\(\left(6 \cdot 10^{21}\right):\left(75 \cdot 10^{18}\right)=\frac{6}{75} \cdot 10^{21-18}=\frac{6}{75} \cdot 10^{3}\)
Trắc nghiệm Toán 6 bài 4 CTST
Chi tiết lời giải: Giải Toán lớp 6 bài 4 Lũy thừa với số mũ tự nhiên Chân trời sáng tạo
3. Giải Toán lớp 6 bài 4 sách Cánh Diều
Toán lớp 6 bài 4 Phép nhân, phép chia các số tự nhiên Cánh Diều bao gồm đáp án chi tiết cho từng phần, từng bài tập trong nội dung chương trình học bài 4 Toán 6, giúp các em học sinh ôn tập, củng cố kiến thức, luyện tập Giải Toán 6 sách Cánh Diều.
Toán lớp 6 trang 21 tập 1 Bài 1
Tìm các số thích hợp ở dấu ?:
a) a . 0 = ?
b) a : 1 = ?
c) 0 : a = ? (với a ≠ 0 )
Đáp án
a) a. 0 = 0
b) a : 1 = a
c) 0 : a = 0
Toán lớp 6 trang 21 tập 1 Bài 2
Tính một cách hợp lí:
a) 50 . 347 . 2
b) 36 . 97 + 97 . 64
c) 157 . 289 - 289 . 57
Đáp án
a) 50 . 347 . 2 = (50 . 2) . 347 = 100 . 347 = 34 700
b) 36 . 97 + 97 . 64 = 97 . (36 + 64) = 97 . 100 = 9 700
c) 157 . 289 - 289 . 57 = 289 . (157 - 57) = 289 . 100 = 28 900
Toán lớp 6 trang 21 tập 1 Bài 3
Đặt tính rồi tính:
a) 409 . 215
b) 54 322 : 346
c) 123 257 : 404
Đáp án
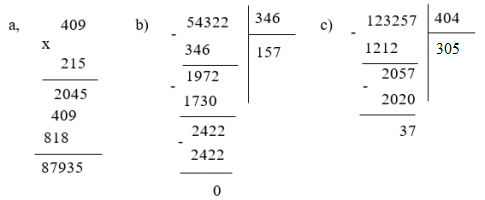
Toán lớp 6 trang 21 tập 1 Bài 4
Một bênh nhân bị sốt cao, mất nước. Bác sĩ chỉ định uống 2 lít dung dịch Oresol để bù nước. Biết mỗi gói Oresol pha với 200 ml nước. Bệnh nhân đó cần dùng bao nhieu gói Oresol?
Đáp án
Đổi: 2 lít = 2000 ml
Bệnh nhân đó cần dùng số gói Oresol là:
2000 : 200 = 10 (gói)
Toán lớp 6 trang 21 tập 1 Bài 5
Một đội thanh niên tình nguyện có 130 người cần thuê ô tô để di chuyển. Họ cần thuê ít nhất bao nhiêu nếu mỗi xe chở được 45 người?
Đáp án
Ta có:
130 : 45 = 2 dư 40
Vậy đội thanh niên cần thuê ít nhất là 3 xe ô tô.
Toán lớp 6 trang 21 tập 1 Bài 6
Lá cây chứa rất nhiều chất diệp lục trong lục lạp làm cho lá cây có màu xanh. Ở lá thầu dầu, cứ 1 mm2 lá có khoảng 500 000 lục lạp (Nguồn: Sinh học 6, NXB Giáo dục Việt Nam, 2010).
Tính số lục lạp có trên một chiếc lá thầu dầu có diện tích khoảng 210 cm2
Ta có: 210 cm2 = 21000 mm2
Số lục lạp có trên một chiếc lá thầu dầu có diện tích khoảng 210 cm2 là:
21000 . 500 000 = 10 500 000 000 (lục lạp)
Toán lớp 6 trang 21 tập 1 Bài 7
Ở Bắc Bộ, quy ước 1 thước = 24m2, 1 sào = 15 thước, 1 mẫu = 10 sào. Theo kinh nghiệm nhà nông, để mạ đạt tiêu chuẩn thì 1 sào ruộng cần gieo khoảng 2 kg thóc giống.
a) Để gieo mạ trên 1 mẫu ruộng cần khoảng bao nhiêu ki-lô-gam thóc giống?
b) Để giao mạ trên 9 ha ruộng cần khoảng bao nhiêu ki-lô-gam thóc giống?
Đáp án
a) 1 mẫu = 10 sào
Để gieo mạ trên 1 mẫu ruộng cần khoảng số ki-lô-gam thóc giống là:
10 . 2 = 20 (kg)
b) 9 ha = 90 000 m2 = 3750 thước = 250 sào
Để gieo mạ trên 9 ha ruộng cần khoảng số ki-lô-gam thóc giống là:
250 . 2 = 500 (kg)
Toán lớp 6 trang 21 tập 1 Bài 8
Sử dụng máy tính cầm tay:

Dùng máy tính cầm tay để tính:
275 x 356; 14 904 : 207; 15 x 47 x 216
Đáp án
Sử dụng máy tính cầm tay tính ta được:
275 x 356 = 97 900
14 904 : 207 = 72
15 x 47 x 216 = 152 280
Trắc nghiệm Toán 6 bài 4 Cánh diều
Chi tiết lời giải: Giải Toán lớp 6 bài 4 Phép nhân, phép chia các số tự nhiên Cánh Diều
Chuyên mục sách mới Toán lớp 6 theo chương trình GDPT









