Phép quay là gì? Hiểu ngay với ví dụ Toán 11
Phép quay Toán 11
Bạn đang tìm cách hiểu nhanh và chính xác phép quay trong chương trình Phép biến hình Toán lớp 11? Bài viết Phép quay là gì? Hiểu ngay với ví dụ Toán 11 sẽ giúp bạn nắm trọn định nghĩa, tính chất và cách vận dụng thông qua các ví dụ trực quan, dễ hiểu. Nội dung được trình bày khoa học, phù hợp cho học sinh muốn hệ thống lại kiến thức hoặc chuẩn bị cho các bài kiểm tra hình học 11.
A. Định nghĩa Phép quay
Cho điểm O và góc lượng giác α. PBH biến điểm O thành chính nó, biến mỗi điểm M ≠ O thành điểm M′ sao cho OM′ = OM và góc (OM; OM′) = α được gọi là phép quay tâm O góc α.
Điểm O: tâm quay.
Góc α: góc quay.
Kí hiệu: Q(O,α).
Nhận xét:
+ Chiều quay dương là chiều dương của đường tròn lượng giác.
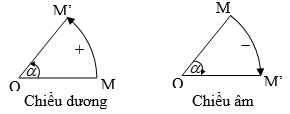
+ Với k ∈ Z:
-
Q(O,2kπ) là phép đồng nhất.
-
Q(O,(2k+1)π) là phép đối xứng tâm O.
B. Tính chất của phép quay
Tính chất 1: Phép quay bảo toàn khoảng cách giữa 2 điểm bất kì.
Tính chất 2: Phép quay biến:
- Đường thẳng → đường thẳng,
- Đoạn thẳng → đoạn thẳng bằng nó,
- Tam giác → tam giác bằng nó,
- Đường tròn → đường tròn có cùng bán kính.
Nhận xét: Giả sử QO,α)(d) = d′. Khi đó:
 \(\left( \widehat{d,d'} \right) =
\left\lbrack \begin{matrix}
\alpha\ \ \ neu\ \ \ \ 0 < \alpha \leq \frac{\pi}{2} \\
\pi - \alpha\ \ \ \ neu\ \ \ \frac{\pi}{2} \leq \alpha < \pi
\end{matrix} \right.\) |
 |
C. Các dạng bài tập Phép quay
Dạng 1. Tìm ảnh của một điểm qua phép quay
Bài 1. Trong mặt phẳng tọa độ \(Oxy\) cho \(A(3;4)\). Hãy tìm tọa độ điểm \(A'\) là ảnh của \(A\) qua phép quay tâm \(O\) góc \(90^{0}\)?
Hướng dẫn giải
Gọi \(B(3;0),C(0;4)\) là tọa độ hình chiếu của \(A\) trên hai trục \(Ox;Oy\). Phép quay tâm \(O\) góc \(90^{0}\) biến hình chóp \(OABC\) thành hình chóp \(OCA'B'\)
Khi đó \(\ C'(0;3),B'( -
4;0)\). Suy ra \(A'( -
4;3)\).
Bài 2. Trong mặt phẳng \(Oxy\) cho điểm \(M(x;y)\). Tìm \(M' = Q_{(O;\varphi)}(M)\)?
Hướng dẫn giải
Hình vẽ minh họa:
Gọi \(M(x;y)\) biết \(OM = r\), góc lượng giác\((Ox;OM) = \alpha\) thì \(M:\left\{ \begin{matrix}
x = r\cos\alpha\ \\
y = r\sin\alpha
\end{matrix} \right.\)
Vì \(M\overset{Q_{(O;\varphi)}}{\rightarrow}M'\) nên \(M'(x';y')\) thì \(\left\{ \begin{matrix}
OM' = \ r \\
(Ox;OM') = \alpha + \varphi\
\end{matrix} \right.\)
Ta có:
\(x' = rcos(\alpha + \varphi) =
r.cos\alpha.cos\varphi - r.sin\alpha.sin\varphi = x\cos\varphi -
y\sin\varphi\ .\)
\(y' = rsin(\alpha + \varphi) =
r.sin\alpha.cos\varphi + r.cos\alpha.sin\varphi = x\sin\varphi +
y\cos\varphi\ .\)
Vậy \(\ M':\left\{ \begin{matrix}
x' = \ x\cos\varphi - y\sin\varphi\ \\
y' = \ x\sin\varphi + y\cos\varphi
\end{matrix} \right.\)
Đặc biệt
\(M\overset{Q_{(O; -
\varphi)}}{\rightarrow}M''\left\{ \begin{matrix}
x'' = x\cos\varphi + y\sin\varphi\ \\
y'' = - x\sin\varphi + y\cos\varphi
\end{matrix} \right.\)
\(M\overset{Q_{(I;\varphi)}}{\rightarrow}M'\left\{
\begin{matrix}
x' - x_{o} = (x - x_{o})cos\varphi - (y - y_{o})sin\varphi\ \\
y' - y_{o} = (x - x_{o})sin\varphi + (y - y_{o})cos\varphi
\end{matrix} \right.\)
\(M\overset{Q_{(I; -
\varphi)}}{\rightarrow}M''\left\{ \begin{matrix}
x'' - x_{o} = (x - x_{o})cos\varphi - (y - y_{o})sin\varphi\ \\
y'' - y_{o} = - (x - x_{o})sin\varphi + (y - y_{o})cos\varphi
\end{matrix} \right.\)
Dạng 2. Tìm ảnh của một đường thẳng
Bài 3. Trong mặt phẳng \(Oxy\) cho đường thẳng \((\Delta):2x - y + 1 =
0\). Tìm ảnh của đường thẳng qua:
a) Phép đối xứng tâm \(I(1; -
2)\).
b) Phép quay \(Q_{\left( O;90^{0}
\right)}\).
Hướng dẫn giải
a) Ta có: \(M'(x';y') = \
D_{I}(M)\) ta có biểu thức toa độ \(M'\left\{ \begin{matrix}
x' = 2 - x \\
y' = - 4 - y
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
x = 2 - x' \\
y = - 4 - y'
\end{matrix} \right.\)
Vì \(M(x;y) \in (\Delta):2x - y + 1 =
0\)
\(\Leftrightarrow 2(2 - x') - ( - 4 -
y') + 1 = 0 \Leftrightarrow - 2x' + y' + 9 = 0\)
\(\Leftrightarrow M'(x';y')
\in (\Delta'):2x - y - 9 = 0\)
Vậy \(\
(\Delta)\overset{D_{I}}{\rightarrow}\ (\Delta'):2x - y - 9 =
0\)
b) Cách 1. Ta có: \(M(x;y)\overset{Q_{(O;90^{0})}}{\rightarrow}M'(x';y')\) biết
Ta có: \((Ox;OM') = \alpha +
90^{0},OM' = r\)
Khi đó: \(M\left\{ \begin{matrix}
x\ = \ r\cos\alpha \\
y\ = \ r\sin\alpha
\end{matrix} \right.\)
\(\overset{Q_{(O;90^{0})}}{\rightarrow}M'\left\{
\begin{matrix}
x' = rcos(\alpha + 90^{\circ}) = - r\sin\alpha = - y \\
y' = rsin(\alpha + 90^{\circ}) = r\cos\alpha = x
\end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix}
x = y' \\
y = - x'
\end{matrix} \right.\)
Vì \(M(x;y) \in (\Delta):2(y') - ( -
x') + 1 = 0 \Leftrightarrow \ x' + 2y' + 1 = 0\)
\(\Leftrightarrow M'(x';y')
\in (\Delta'):x + 2y + 1 = 0\)
Vậy \(\
(\Delta)\overset{Q_{(O;90^{\circ})}}{\rightarrow}(\Delta'):x + 2y +
1 = 0\)
Cách 2.
\(M(0;1) \in (\Delta)\
I\overset{Q_{(O;90^{\circ})}}{\rightarrow}M'( - 1;0) \in
(\Delta')\)
\(N\left( - \frac{1}{2};0 \right) \in
(\Delta)\overset{Q_{(O;90^{\circ})}}{\rightarrow}N'\left( 0;\frac{-
1}{2} \right) \in (\Delta')\)
\((\Delta)\overset{Q_{(O;90^{\circ})}}{\rightarrow}(\Delta')
\equiv M'N':x + 2y + 1 = 0\)
Cách 3.
Vì \((\Delta)\
\overset{Q_{(O;90^{\circ})}}{\rightarrow}(\Delta') \Rightarrow
(\Delta)\bot(\Delta')\) mà hệ số góc \(k_{\Delta} = 2 \Rightarrow k_{\Delta'} = -
\frac{1}{2}\)
\(M(0;1) \in (\Delta)\
I\overset{Q_{(O;90^{\circ})}}{\rightarrow}M'(1;0) \in (\Delta')\)
\((\Delta'):\left\{ \begin{matrix}
Qua\ M'(1;0) \\
hsg:k\ = - \frac{1}{2}
\end{matrix} \right.\ \Rightarrow (\Delta'):x + 2y + 1 =
0\)
Dạng 3. Tìm ảnh của một đường tròn
Bài 4. Trong mặt phẳng tọa độ \(Oxy\) cho phép quay \(Q_{\left( O;45^{0} \right)}\). Tìm ảnh của:
a) Điểm \(A(2;2)\).
b) Đường tròn \((x - 1)^{2} + y^{2} =
4\).
Hướng dẫn giải
Gọi \(M(x;y)\overset{Q_{(O;45^{0})}}{\rightarrow}M'(x';y')\)
Ta có: \(OM = 2\sqrt{2},(Ox;OM) =
\alpha\)
Khi đó tọa độ điểm M’(x’; y’) được xác định như sau:
\(x' = rcos(\alpha + 45^{\circ}) =
r\cos\alpha.cos45^{\circ} - r\sin\alpha.sin45^{\circ} = x.cos45^{\circ}
- y.sin45^{\circ}\)
\(y' = rsin(\alpha + 45^{\circ}) =
r\sin\alpha.cos45^{\circ} + r\cos\alpha.sin45^{\circ} = y.cos45^{\circ}
+ x.sin45^{\circ}\)
\(\Rightarrow M':\left\{
\begin{matrix}
x' = \frac{\sqrt{2}}{2}x - \frac{\sqrt{2}}{2}y \\
y' = \frac{\sqrt{2}}{2}x + \frac{\sqrt{2}}{2}y
\end{matrix} \right.\)
a) \(A(2;2)\
\overset{Q_{(O;45^{\circ})}}{\rightarrow}A'(0\ ;2\sqrt{2})\)
b) Vì đường tròn có tâm \(I(1;0)\) và bán kính \(R\ = \ 2\) nên qua \(Q_{(O\ \ ;\ \ 45^{\circ})}\) ta được đường tròn \((C')\) tâm \(I'\) và bán kính \(R'\ = \ R\ = \ 2\)
\(I(1;0)\overset{Q_{(O;45^{\circ})}}{\rightarrow}I'\left(
\frac{\sqrt{2}}{2};\frac{\sqrt{2}}{2} \right)\)
Vậy \((C'):\left( x -
\frac{\sqrt{2}}{2} \right)^{2} + \left( y - \frac{\sqrt{2}}{2}
\right)^{2} = 4\)
---------------------------------------
Hy vọng bài viết đã giúp bạn hiểu rõ bản chất phép quay, nắm được quy tắc áp dụng cũng như nhận diện nhanh các dạng bài thường gặp trong Toán 11. Hãy tiếp tục luyện tập thêm ở các chuyên đề khác thuộc phép biến hình lớp 11 để học vững – hiểu sâu – làm bài hiệu quả hơn. Chúc bạn học tốt và chinh phục điểm cao!
