Cho tam giác đều. Hỏi hình tam giác đều
có bao nhiêu trục đối xứng:
Tam giác đều có đúng 3 trục đối xứng.
Bạn đang tìm tài liệu luyện tập giúp nắm chắc kiến thức về phép đối xứng trục trong chương trình Toán 11? Bộ Trắc nghiệm Phép đối xứng trục Toán 11 – Có lời giải chi tiết dưới đây được thiết kế theo chuẩn bài tập online, kèm đáp án và hướng dẫn giải rõ ràng. Tài liệu hỗ trợ học sinh củng cố lý thuyết, nhận biết dạng bài và rèn kỹ năng làm trắc nghiệm nhanh – chính xác, phù hợp cho ôn tập thường xuyên hoặc chuẩn bị kiểm tra.
Cho tam giác đều. Hỏi hình tam giác đều
có bao nhiêu trục đối xứng:
Tam giác đều có đúng 3 trục đối xứng.
Trong mặt phẳng với hệ trục tọa độ . Cho phép đối xứng trục
, với
gọi
là ảnh của
qua phép đối xứng trục
. Khi đó tọa độ điểm
là:
Hai điểm đối xứng nhau qua trục có tung độ bằng nhau và hoành độ đối nhau.
Trong mặt phẳng với hệ trục tọa độ , cho phép đối xứng trục
. Với bất kì, gọi
là ảnh của
qua phép đối xứng trục
. Khi đó tọa độ điểm
là:
Hai điểm đối xứng nhau qua trục có hoành độ bằng nhau và tung độ đối nhau.
Trong mặt phẳng cho điểm
. Hỏi
là ảnh của điểm nào trong các điểm sau qua phép đối xứng trục
?
Gọi là ảnh của điểm
qua phép đối xứng trục
ta có:
.
Vậy .
Trong mặt phẳng , cho Parapol
có phương trình
. Hỏi Parabol nào trong các parabol sau là ảnh của
qua phép đối xứng trục
?
Gọi là ảnh của điểm
qua phép đối xứng trục
ta có:
.
Vậy .
Cho hình vuông có hai đường chéo
và
cắt nhau tại
. Hãy chọn phát biểu đúng trong các phát biểu sau đây.
Xét phát biểu “Hai điểm và
đối xứng nhau qua trục
”. Sai.
Xét phát biểu “Phép đối xứng trục biến
thành
”. Sai, phép đối xứng trục
biến điểm
thành chính nó.
Xét phát biểu “Phép đối xứng trục biến
thành
”. Đúng.
Xét phát biểu “Hình vuông chỉ có 2 trục đối xứng là
và
”. Hình vuông có 4 trục đối xứng.
Giả sử rằng qua phép đối xứng trục (
là trục đối xứng), đường thẳng
biến thành đường thẳng
. Hãy chọn câu sai trong các câu sau:
Ta có vuông góc với
thì
trùng với
. Ngược lại
trùng với
thì
có thể trùng
.
Trong mặt phẳng cho điểm
. Hỏi trong bốn điểm sau điểm nào là ảnh của
qua phép đối xứng trục
?
Gọi là ảnh của điểm
qua phép đối xứng trục
ta có:
.
Vậy .
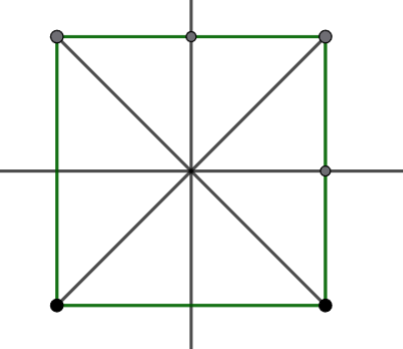
Hình vuông có mấy trục đối xứng?
Hình vuông có 4 trục đối xứng.
Hình gồm hai đường thẳng và
vuông góc với nhau đó có mấy trục đối xứng?
Hình vẽ minh họa:
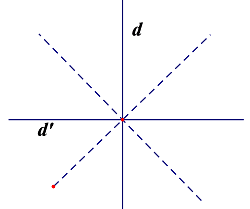
Ta có trục đối xứng là
đường thẳng đó và
đường phân giác tạo bởi
đường thẳng đó.
Trong mặt phẳng , cho parabol
. Hỏi parabol nào sau đây là ảnh của parabol
qua phép đối xứng trục
?
Gọi là ảnh của điểm
qua phép đối xứng trục
ta có:
.
Vậy .
Tìm mệnh đề sai trong các mệnh đề sau:
Dựa vào các tính chất của phép đối xứng trục ta có câu "Phép đối xứng trục biến một đường thẳng thành một đường thẳng song song hoăc trùng với đường thẳng đã cho" sai.
Phát biểu nào sau đây là đúng về phép đối xứng trục :
Xét phát biểu “Phép đối xứng trục biến
thành
(I là giao điểm của
và trục d): Chiều ngược lại sai khi
không vuông góc với
Xét phát biểu” Nếu thuộc
thì
” Đúng, phép đối xứng trục giữ bất biến các điểm thuộc trục đối xứng.
Xét phát biểu “Phép đối xứng trục không phải là phép dời hình “ Sai, phép đối xứng trục là phép dời hình.
Xét phát biểu “Phép đối xứng trục biến
thành
” Sai, cần
tại trung điểm của
mới suy ra được
là ảnh của
qua phép đối xứng trục
, tức là cần
là trung trực của
Trong các mệnh đề sau mệnh đề nào đúng?
Các đường kính của đường tròn là các trục đối xứng.
Trong mặt phẳng , qua phép đối xứng trục
. Điểm
biến thành điểm nào trong các điểm sau?
Gọi là ảnh của điểm
qua phép đối xứng trục
ta có:
.
Vậy .
Trong mặt phẳng với hệ trục tọa độ , cho phép đối xứng trục
. Phép đối xứng trục
biến đường tròn
thành đường tròn
có phương trình là:
có tâm
và bán kính bằng 1.
Gọi là ảnh của
qua phép đối xứng trục
.
Khi đó, là trung trực của
.
Gọi là trung điểm của
.
Do đó .
Phép đối xứng trục biến đường tròn thành đường tròn có cùng bán kính nên ảnh của là :
Trong mặt phẳng với hệ trục tọa độ . Phép đối xứng trục
biến đường tròn
thành đường tròn
có phương trình là:
Gọi là ảnh của
qua phép đối xứng trục
. Khi đó:
Vậy thuộc đường tròn
có phương trình
Trong mặt phẳng cho parabol
có phương trình
. Hỏi parabol nào trong các parabol sau là ảnh của
qua phép đối xứng trục
?
Gọi là ảnh của điểm
qua phép đối xứng trục
ta có:
.
Vậy .
Hình gồm hai đường tròn có tâm và bán kính khác nhau (không giao nhau) có bao nhiêu trục đối xứng?
Hình vẽ minh họa
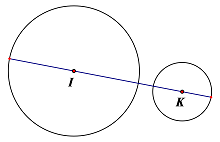
Vậy kết quả đúng là một trục đối xứng.
Trong mặt phẳng cho điểm
. Hỏi trong bốn điểm sau điểm nào là ảnh của
qua phép đối xứng qua đường thẳng
?
Gọi là ảnh của điểm
qua phép đối xứng qua
.
Gọi là đường thẳng đi qua điểm
và vuông góc
ta có:
.
Gọi thì
.
Khi đó là trung điểm của
nên suy ra
.
Cho đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình
. Hỏi
có mấy trục đối xứng?
Hình vẽ minh họa:
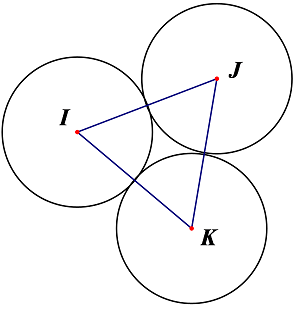
Gọi lần lượt là tâm của
đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình
.
Trục đối xứng của hình là các đường cao của tam giác đều
.
Trong các mệnh đề sau, mệnh đề nào đúng?
Thực hiện liên tiếp hai phép tịnh tiến sẽ được một phép tịnh tiến trong đó vec tơ tịnh tiến bằng tổng của 2 vec tơ tịnh tiến của hai phép đã cho.
Hình nào sau đây có trục đối xứng (mỗi hình là một chữ cái in hoa):
Hình có trục đối xứng là M.
Cho các chữ cái in hoa . Khẳng định nào sau đậy đúng?
Hình có một trục đối xứng: . Hình có hai trục đối xứng:
.
Hình nào sau đây có trục đối xứng:
Hình có trục đối xứng là tam giác cân.
Trong mặt phẳng với hệ trục tọa độ , cho phép đối xứng trục
. Phép đối xứng trục
biến đường thẳng
thành đường thẳng
có phương trình là:
Gọi là ảnh của
qua phép đối xứng trục
. Khi đó:
Vậy thuộc đường thẳng
có phương trình
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
