Tổng hợp bài tập Phép quay Toán 11 – Có đáp án và giải chi tiết

Bạn đang tìm trọn bộ bài tập giúp nắm vững kiến thức phép quay trong chương trình Toán 11? Tài liệu Tổng hợp bài tập Phép quay Toán 11 – Có đáp án và giải chi tiết dưới đây sẽ hỗ trợ bạn luyện tập theo từng mức độ, từ cơ bản đến vận dụng. Mỗi câu hỏi đều kèm lời giải rõ ràng, giúp bạn hiểu đúng bản chất phép biến hình và áp dụng chính xác vào bài tập. Đây là nguồn tài liệu lý tưởng cho học sinh muốn ôn tập, tự học hoặc chuẩn bị kiểm tra.

A. ĐỀ BÀI TRẮC NGHIỆM

Câu 1. Trong mặt phẳng cho hình vuông \(ABCD\) có tâm \(O\), góc \(\left( \overrightarrow{DC},\ \ \overrightarrow{DA} \right) = 90^{o}\). Khi đó ảnh của điểm \(B\) qua phép quay tâm \(O\) góc quay \(- 90^{o}\) là điểm nào?

A. \(C\).       B. \(A\).           C. Là \(M \notin \left\{ A,\ \ C,\ \ D,\ \ O \right\}\).       D. \(D\).

Câu 2. Trong mặt phẳng \(Oxy\), quay \(Q_{\left( O,90^{{^\circ}} \right)}\), \(M'(2;3)\) là ảnh của điểm

A. \(M(3; - 2)\).        B. \(M(3;2)\).        C. \(M( - 2; - 3)\).      D. \(M( - 3; - 2)\).

Câu 3. Trong mặt phẳng \(Oxy\), điểm \(M(2;3)\) có ảnh là điểm nào qua phép quay tâm \(O\) góc quay \(90{^\circ}\)?

A. \(M'(3; - 2)\).       B. \(M'( - 2; - 3)\).      C. \(M'(2; - 3)\).       D. \(M'( - 3;2)\).

Câu 4. Cho điểm \(A(1; - 3)\). Hỏi điểm nào trong các điểm sau là ảnh của \(A\) qua phép quay tâm \(O\) góc quay \(90{^\circ}\)?

A. \(( - 3; - 1)\).      B. \(( - 6; - 2)\).      C. \((6;2)\).      D. \((3;1)\)

Câu 5. Cho tam giác đều \(ABC\). Hãy xác định góc quay của phép quay tâm \(A\) biến \(B\) thành \(C.\)

A. \(\varphi = 30{^\circ}\).                   B. \(\varphi = 60{^\circ}\) hoặc \(\varphi = - 60{^\circ}\).

C. \(\varphi = - 120{^\circ}\).               D. \(\varphi = 90{^\circ}\).

Câu 6. Ảnh của đường thẳng \(d:x - y - 2 = 0\) qua phép quay tâm \(O\) góc quay \(- 90^{0}\) là đường thẳng \(d'\) có phương trình

A. \(x - y - 2 = 0\).       B. \(x - y + 2 = 0\).      C. \(x + y + 2 = 0\).      D. \(x + y - 2 = 0\).

Câu 7. Tìm tọa độ của điểm \(M'\) là ảnh của điểm \(M(1;0)\) qua phép quay tâm \(O(0;0)\) góc quay \(90{^\circ}\)?

A. \(M'(1;1)\).      B. \(M'(0; - 1)\).      C. \(M'(1;0)\).      D. \(M'(0;1)\).

Câu 8. Trong mặt phẳng \(Oxy\), cho điểm \(B( - 3;6)\). Tìm tọa độ điểm \(E\) sao cho \(B\) là ảnh của \(E\) qua phép quay tâm \(O\), góc quay \(90{^\circ}\)

A. \(E(6;3)\).     B. \(E( - 3;\ \ - 6)\).     C. \(E( - 6; - 3)\).      D. \(E(3;\ \ 6)\).

Câu 9. Trong mặt phẳng \(Oxy\), cho đường thẳng \(d:5x - 3y + 15 = 0\). Viết phương trình của đường thẳng \(d'\) là ảnh của đường thẳng \(d\) qua phép quay tâm \(O\) góc \(90{^\circ}\).

A. \(5x + 3y - 15 = 0\).           B. \(5x + 3y + 15 = 0\).

C. \(3x + 5y - 15 = 0\).           D. \(3x + 5y + 15 = 0\).

Câu 10. Trong mặt phẳng tọa độ \(Oxy\) cho phép quay tâm \(O\) biến điểm \(A(1;0)\) thành điểm \(A'(0;1)\). Khi đó nó biến điểm \(M(1; - 1)\) thành điểm:

A. \(M'( - 1; - 1)\).        B. \(M'(1;1)\).          C. \(M'( - 1;1)\).         D. \(M'(1;1)\).

Câu 11. Trong mặt phẳng \(Oxy\) cho đường thẳng \(d:x - y - 4 = 0\). Viết phương trình đường thẳng \(d'\) với \(d'\) là ảnh của \(d\) qua phép quay tâm \(I(1;1)\) góc quay \(- \frac{\pi}{2}\).

A. \(d':x - y - 1 = 0\).             B. \(d':x + y + 2 = 0\).

C. \(d':x - y - 2 = 0\).            D. \(d':x + y - 2 = 0\).

Câu 12. Trong mặt phẳng tọa độ \(Oxy\) cho đường thẳng có \(d:2x - y + 1 = 0\), ảnh \(d'\) của \(d\)qua phép quay tâm O, góc quay \(- 90^{0}\) là:

A. \(d':x - 2y - 1 = 0\)                    B. \(d':x + 2y - 1 = 0\)

C. \(d':2x - y + 1 = 0\)                   D. \(d':x + 2y + 1 = 0\)

Câu 13. Trong mặt phẳng Oxy, ảnh của điểm \(M( - 6;1)\)qua phép quay \(Q_{\left( O,90^{o} \right)}\) là:

A.\(M'( - 1; - 6)\) .           B. \(M'(1;6)\).             C. \(M'( - 6; - 1)\).            D. \(M'(6;1)\).

Câu 14. Trong mặt phẳng Oxy, qua phép quay \(Q_{\left( O,90^{o} \right)}\), \(M'(3; - 2)\) là ảnh của điểm :

A.\(M(3;2)\) .           B. \(M(2;3)\).          C. \(M( - 3; - 2)\).        D. \(M( - 2; - 3)\).

Câu 15. Trong mặt phẳng Oxy, ảnh của điểm \(M(3;4)\)qua phép quay \(Q_{\left( O,45^{o} \right)}\) là:

A.\(M'\left( \frac{7\sqrt{2}}{2};\frac{7\sqrt{2}}{2} \right)\) .                  B. \(M'\left( - \frac{\sqrt{2}}{2};\frac{7\sqrt{2}}{2} \right)\).

C. \(M'\left( - \frac{\sqrt{2}}{2}; - \frac{\sqrt{2}}{2} \right)\).                 D. \(M'\left( \frac{7\sqrt{2}}{2}; - \frac{\sqrt{2}}{2} \right)\).

(Còn tiếp)

B. BẢNG ĐÁP ÁN TỔNG QUÁT

C. HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1:

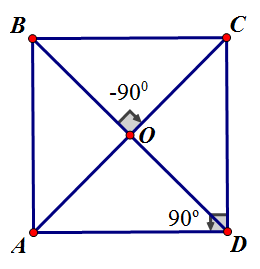
Vì \(\left( \overrightarrow{DC},\ \ \overrightarrow{DA} \right) = 90^{o}\) nên thứ tự các điểm \(A,\ \ B,\ \ C,\ \ D\) cùng chiều kim đồng hồ.

Do đó \(Q_{\left( O;\ \ - 90^{o} \right)}(B) = C\).

Câu 2: Ta có \(Q_{\left( 0, - 90^{{^\circ}} \right)}\left( M' \right) = M(x;y)\). Tọa độ \(M\) là \(\left\{ \begin{matrix} x = 3 \\ y = - 2 \end{matrix} \right.\).

Câu 3: Gọi \(M'(x';y')\) là ảnh của điểm \(M(x;y)\) qua phép quay tâm \(O\) góc quay \(90{^\circ}\).

Khi đó ta có \(\left\{ \begin{matrix} x' = - y \\ y' = x \end{matrix} \right.\).

Áp dụng công thức trên ta có.

Điểm \(M(2;3)\) có ảnh là điểm \(M'( - 3;2)\) qua phép quay tâm \(O\) góc quay \(90{^\circ}\).

Câu 4: Qua \(Q_{(O;90{^\circ})}(A) = A' \Leftrightarrow \overrightarrow{OA}.\overrightarrow{OA'} = 0 \Rightarrow A'(3;1)\).

Câu 5:

Ta có \(\widehat{BAC} = 60{^\circ}\) nên để phép quay tâm \(A\) với góc quay \(\varphi\) biến \(B\) thành \(C\) thì \(\varphi = 60{^\circ}\) hoặc \(\varphi = - 60{^\circ}\) ⇒

Câu 6: Có \(d':x + y + c = 0\). Lấy \(A(2;0) \in d\). Gọi \(A' = Q_{\left( O; - 90^{0} \right)}\) thì \(A'(0; - 2)\).

Do \(A' \in d'\) nên \(- 2 + c = 0 \Rightarrow c = 2\).

Câu 7: \(\left. \ \begin{matrix} M(1;0) \in Ox \\ Q_{\left( O;90^{0} \right)}(M) = M' \end{matrix} \right\} \Leftrightarrow \left\{ \begin{matrix} M' \in Oy \\ OM' = OM = 1 \end{matrix} \right.\ \Leftrightarrow M'(0;1)\).

Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!

----------------------------------------------

Hy vọng bộ bài tập và lời giải chi tiết đã giúp bạn củng cố toàn diện kiến thức về phép quay trong Toán 11. Hãy tiếp tục sử dụng chuyên đề này như tài liệu luyện tập thường xuyên để cải thiện tốc độ, tư duy hình học và tự tin khi làm bài kiểm tra. Đừng quên khám phá thêm nhiều chủ đề trong mục Bài tập Toán 11 có đáp án để học hiệu quả hơn mỗi ngày!