VnDoc.com

Bài tập tính Giới hạn dãy số dạng lũy thừa

Chuyên đề Giới hạn của dãy số Toán 11

Bài trước

Tải về

Bài sau

Lớp: Lớp 11

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại: Tài liệu Lẻ

Mức độ: Trung bình

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Chuyên đề giới hạn dãy số Toán 11 dạng lũy thừa

A. Cách tính giới hạn dãy dạng lũy thừa
B. Bài tập minh họa tính giới hạn dãy số dạng lũy thừa
C. Bài tập vận dụng tự rèn luyện có đáp án chi tiết

Trong chuyên đề Giới hạn của dãy số Toán 11, các bài tập tính giới hạn dãy số dạng lũy thừa đóng vai trò quan trọng trong việc phân tích tốc độ tăng – giảm của dãy. Dạng toán này thường yêu cầu học sinh nhận diện cơ số, số mũ và so sánh mức độ tăng trưởng để suy ra giới hạn chính xác. Bài viết dưới đây sẽ tổng hợp các dạng bài tiêu biểu, giúp bạn luyện tập có hệ thống và hiệu quả.

A. Cách tính giới hạn dãy dạng lũy thừa

Phương pháp: Tính giới hạn $\lim\frac{f(n)}{g(n)}$ $\lim\frac{f(n)}{g(n)}$ trong đó $f(n)$ và $g(n)$là các lũy thừa dạng $X^{n}$ $X^{n}$

Bước 1: Đưa biểu thức về cùng số mũ $n$.
Bước 2: Chia tử và mẫu số cho $a^{n}$ $a^{n}$trong đó $a$ là số có trị tuyệt đối lớn nhất.
Bước 3: Áp dụng kết quả “ Nếu $|q| < 1$ thì $\lim q^{n} = 0$ $\lim q^{n} = 0$”.

B. Bài tập minh họa tính giới hạn dãy số dạng lũy thừa

Bài tập 1: Tính các giới hạn sau đây:

a) $\lim\left( 2^{n} + 3^{n} \right)$ $\lim\left( 2^{n} + 3^{n} \right)$ b) $\lim\left( \frac{4.3^{n} - 2^{n}}{2.5^{n} + 4^{n}} \right)$ $\lim\left( \frac{4.3^{n} - 2^{n}}{2.5^{n} + 4^{n}} \right)$ c) $\lim\left( \frac{7^{n} + 1}{- 2.3^{n} - 3.6^{n}} \right)$ $\lim\left( \frac{7^{n} + 1}{- 2.3^{n} - 3.6^{n}} \right)$

d) $\lim\left( \frac{5^{n + 1} - 4^{n} + 1}{2.5^{n} - 6^{n}} \right)$ $\lim\left( \frac{5^{n + 1} - 4^{n} + 1}{2.5^{n} - 6^{n}} \right)$ e) $\lim\frac{1 + 3 + 3^{2} + \cdots + 3^{n}}{2 \cdot 3^{n + 1} + 2^{n}}$ $\lim\frac{1 + 3 + 3^{2} + \cdots + 3^{n}}{2 \cdot 3^{n + 1} + 2^{n}}$

Hướng dẫn giải

a) Ta có:

$\lim\left( 2^{n} + 3^{n} \right) = \lim 3^{n}\left\lbrack \left( \frac{2}{3} \right)^{n} + 1 \right\rbrack = + \infty.$ $\lim\left( 2^{n} + 3^{n} \right) = \lim 3^{n}\left\lbrack \left( \frac{2}{3} \right)^{n} + 1 \right\rbrack = + \infty.$

b) Ta có:

$\lim\left( \dfrac{4 \cdot 3^{n} -2^{n}}{3 \cdot 5^{n} + 4^{n}} \right) = \lim\left( \dfrac{\dfrac{4 \cdot3^{n} - 2^{n}}{5^{n}}}{\dfrac{3 \cdot 5^{n} + 4^{n}}{5^{n}}}\right)$ $\lim\left( \dfrac{4 \cdot 3^{n} -2^{n}}{3 \cdot 5^{n} + 4^{n}} \right) = \lim\left( \dfrac{\dfrac{4 \cdot3^{n} - 2^{n}}{5^{n}}}{\dfrac{3 \cdot 5^{n} + 4^{n}}{5^{n}}}\right)$ $= \lim\left( \dfrac{4 \cdot\dfrac{3^{n}}{5^{n}} - \dfrac{2^{n}}{5^{n}}}{2 + \dfrac{4^{n}}{5^{n}}}\right) = 0$ $= \lim\left( \dfrac{4 \cdot\dfrac{3^{n}}{5^{n}} - \dfrac{2^{n}}{5^{n}}}{2 + \dfrac{4^{n}}{5^{n}}}\right) = 0$

c) Ta có:

$\lim\left( \frac{7^{n} + 1}{- 2 \cdot3^{n} - 3 \cdot 6^{n}} \right) = \lim\left( \dfrac{\dfrac{7^{n} +1}{7^{n}}}{\dfrac{- 2 \cdot 3^{n} - 3 \cdot 6^{n}}{7^{n}}}\right)$ $\lim\left( \frac{7^{n} + 1}{- 2 \cdot3^{n} - 3 \cdot 6^{n}} \right) = \lim\left( \dfrac{\dfrac{7^{n} +1}{7^{n}}}{\dfrac{- 2 \cdot 3^{n} - 3 \cdot 6^{n}}{7^{n}}}\right)$ $= \lim\left( \dfrac{1 +\dfrac{1}{7^{n}}}{- 2 \cdot \dfrac{3^{n}}{7^{n}} - 3 \cdot\dfrac{6^{n}}{7^{n}}} \right) = - \infty$ $= \lim\left( \dfrac{1 +\dfrac{1}{7^{n}}}{- 2 \cdot \dfrac{3^{n}}{7^{n}} - 3 \cdot\dfrac{6^{n}}{7^{n}}} \right) = - \infty$

d) Ta có:

$\lim\left( \dfrac{5^{n + 1} - 4^{n} +1}{2.5^{n} - 6^{n}} \right) = \lim\left( \dfrac{\dfrac{5^{n + 1} - 4^{n} +1}{6^{n}}}{\dfrac{2.5^{n} - 6^{n}}{6^{n}}} \right)$ $\lim\left( \dfrac{5^{n + 1} - 4^{n} +1}{2.5^{n} - 6^{n}} \right) = \lim\left( \dfrac{\dfrac{5^{n + 1} - 4^{n} +1}{6^{n}}}{\dfrac{2.5^{n} - 6^{n}}{6^{n}}} \right)$ $= \lim\frac{5.\left( \dfrac{5}{6}\right)^{n} - \left( \dfrac{2}{3} \right)^{n} + \left( \dfrac{1}{6}\right)^{n}}{2.\left( \dfrac{5}{6} \right)^{n} - 1} = 0$ $= \lim\frac{5.\left( \dfrac{5}{6}\right)^{n} - \left( \dfrac{2}{3} \right)^{n} + \left( \dfrac{1}{6}\right)^{n}}{2.\left( \dfrac{5}{6} \right)^{n} - 1} = 0$

e) Ta có:

$\lim\dfrac{1 + 3 + 3^{2} + \cdots +3^{n}}{2 \cdot 3^{n + 1} + 2^{n}}$ $\lim\dfrac{1 + 3 + 3^{2} + \cdots +3^{n}}{2 \cdot 3^{n + 1} + 2^{n}}$ $= \lim\frac{1 - \dfrac{3}{2}\left( 1 -3^{n} \right)}{2 \cdot 3^{n + 1} + 2^{n}} = \dfrac{1}{4}$ $= \lim\frac{1 - \dfrac{3}{2}\left( 1 -3^{n} \right)}{2 \cdot 3^{n + 1} + 2^{n}} = \dfrac{1}{4}$

Bài tập 2: Cho dãy số $\left( u_{n} \right)$ $\left( u_{n} \right)$, xác định bởi: $u_{1} = 1;u_{n + 1} = \frac{u_{n} - 4}{u_{n} + 6}$ $u_{1} = 1;u_{n + 1} = \frac{u_{n} - 4}{u_{n} + 6}$. $\forall n \geq 1$ $\forall n \geq 1$. Tính giới hạn $\lim\frac{u_{n} + 1}{u_{n} + 4}$ $\lim\frac{u_{n} + 1}{u_{n} + 4}$.

Hướng dẫn giải

Đặt $v_{n} = \frac{u_{n} + 1}{u_{n} + 4}$ $v_{n} = \frac{u_{n} + 1}{u_{n} + 4}$.

Ta có: $v_{n + 1} = \frac{u_{n + 1} + 1}{u_{n + 1} + 4} = \frac{2\left( u_{n} + 1 \right)}{5\left( u_{n} + 4 \right)} = \frac{2}{5}v_{n} = ... = \left( \frac{2}{5} \right)^{n + 1}.$ $v_{n + 1} = \frac{u_{n + 1} + 1}{u_{n + 1} + 4} = \frac{2\left( u_{n} + 1 \right)}{5\left( u_{n} + 4 \right)} = \frac{2}{5}v_{n} = ... = \left( \frac{2}{5} \right)^{n + 1}.$

Vậy, ta có: $v_{n} = \left( \frac{2}{5} \right)^{n}$ $v_{n} = \left( \frac{2}{5} \right)^{n}$do đó $\lim\frac{u_{n} + 1}{u_{n} + 4} = \lim v_{n} = 0$ $\lim\frac{u_{n} + 1}{u_{n} + 4} = \lim v_{n} = 0$.

C. Bài tập vận dụng tự rèn luyện có đáp án chi tiết

Bài tập 1: Tính các giới hạn sau đây:

a) $\lim\left\lbrack - 4^{n} + ( - 2)^{n} \right\rbrack$ $\lim\left\lbrack - 4^{n} + ( - 2)^{n} \right\rbrack$ b) $\lim\left( \frac{1 + 3^{n}}{3.3^{n} + 2^{n}} \right)$ $\lim\left( \frac{1 + 3^{n}}{3.3^{n} + 2^{n}} \right)$ c) $\lim\frac{1 + \frac{1}{3} + \left( \frac{1}{3} \right)^{2} + \cdots + \left( \frac{1}{3} \right)^{n}}{1 + \frac{2}{5} + \left( \frac{2}{5} \right)^{2} + \cdots + \left( \frac{2}{5} \right)^{n}}$ $\lim\frac{1 + \frac{1}{3} + \left( \frac{1}{3} \right)^{2} + \cdots + \left( \frac{1}{3} \right)^{n}}{1 + \frac{2}{5} + \left( \frac{2}{5} \right)^{2} + \cdots + \left( \frac{2}{5} \right)^{n}}$

d) $\lim\frac{3^{n} - 2.5^{n + 1}}{2^{n + 1} + 5^{n}}$ $\lim\frac{3^{n} - 2.5^{n + 1}}{2^{n + 1} + 5^{n}}$ e) $\lim\frac{( - 1)^{n}2^{5n + 1}}{3^{5n + 2}}$ $\lim\frac{( - 1)^{n}2^{5n + 1}}{3^{5n + 2}}$ f) $\lim\frac{3^{n} - 4.2^{n + 1} - 3}{3.2^{n} + 4^{n}}.$ $\lim\frac{3^{n} - 4.2^{n + 1} - 3}{3.2^{n} + 4^{n}}.$

Bài tập 2: Cho dãy số $\left( u_{n} \right)$ $\left( u_{n} \right)$, xác định bởi: $u_{1} = 3,u_{n + 1} = \frac{u_{n} + 1}{2},\forall n \geq 1$ $u_{1} = 3,u_{n + 1} = \frac{u_{n} + 1}{2},\forall n \geq 1$. Tính giới hạn $\lim u_{n}$ $\lim u_{n}$.

Bài tập 3: Có bao nhiêu giá trị nguyên của $a$ thuộc $(0;20)$ sao cho $\lim\sqrt{3 + \frac{an^{2} - 1}{3 + n^{2}} - \frac{1}{2^{n}}}$ $\lim\sqrt{3 + \frac{an^{2} - 1}{3 + n^{2}} - \frac{1}{2^{n}}}$ là một số nguyên.

Bài tập 4. Tính giới hạn $L = \lim\left\lbrack \frac{\left( 3^{n} + 2 \right)\left( 2^{n} + 1 \right)}{3^{n} + 2} - 2^{n} + 2 \right\rbrack$ $L = \lim\left\lbrack \frac{\left( 3^{n} + 2 \right)\left( 2^{n} + 1 \right)}{3^{n} + 2} - 2^{n} + 2 \right\rbrack$.

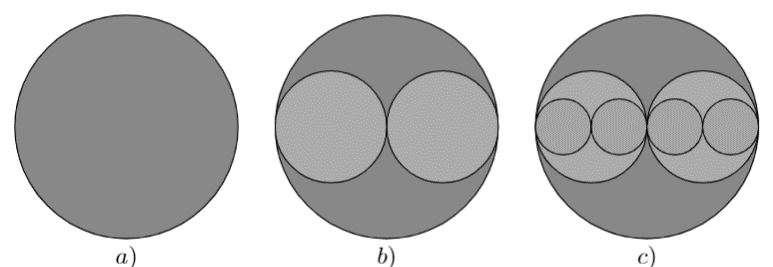
Bài tập 5: Từ tờ giấy, cắt một hình tròn bán kính $R = 2\ (cm)$ $R = 2\ (cm)$ như Hình $3a$. Tiếp theo, cắt hai hình tròn bán kính $\frac{R}{2}$ $\frac{R}{2}$ chồng lên hình tròn đầu tiên như Hình $3b$. Tiếp theo, cắt bốn hình tròn bán kính $\frac{R}{4}$ $\frac{R}{4}$ rồi chồng lên các hình trước như hình c). Cứ thế tiếp tục mãi. Tính tổng diện tích của các hình tròn (làm tròn kết quả đến hàng phần chục).

-----------------------------------------

Khi hiểu rõ bản chất của dãy số dạng lũy thừa, việc tính giới hạn sẽ trở nên nhanh chóng và chính xác hơn. Hy vọng chuyên đề này sẽ giúp học sinh củng cố kiến thức và tự tin giải các bài giới hạn dãy số Toán 11 trong học tập cũng như kiểm tra.

Xem thử Tải về

Chọn file muốn tải về: