Cách tính góc giữa hai mặt phẳng – Hướng dẫn chuẩn từng bước
Cách tính góc giữa 2 mặt phẳng
Trong hình học không gian, tính góc giữa hai mặt phẳng là dạng toán quan trọng nhưng dễ nhầm lẫn nếu không xác định đúng bản chất hình học. Việc dựng đường vuông góc hợp lý chính là chìa khóa giúp xác định góc một cách chính xác và ngắn gọn.
Bài viết này sẽ hướng dẫn cách tính góc giữa hai mặt phẳng theo từng bước rõ ràng, giúp học sinh hiểu đúng phương pháp, tránh sai sót thường gặp và áp dụng hiệu quả khi làm bài.
A. Công thức tính góc giữa hai mặt phẳng
a) Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
\(\left. \ \begin{matrix}
a\bot(\alpha) \\
b\bot(\beta)
\end{matrix} \right\} \Rightarrow \left( (\alpha),(\beta) \right) =
(a,b)\)
b) Trong trường hợp 2 mặt phẳng cắt nhau: “Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến tại một điểm”.
B. Ứng dụng khoảng cách để tính góc giữa hai mặt phẳng
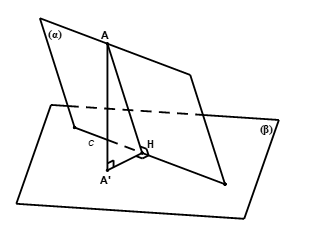
Gọi \(\varphi = \left( (\alpha),\ (\beta)
\right)\) và \(c = (\alpha) \cap
(\beta)\).
Ta có:
\(\sin\varphi = \frac{AA'}{AH} =
\frac{d\left( A,(\beta) \right)}{d(A,c)}\)
Như vậy, bài toán tính góc giữa hai mặt phẳng có thể quy về bài toán tính khoảng cách từ một điểm đến một mặt phẳng và tính khoảng cách từ một điểm đến một đường thẳng.
C. Bài tập minh họa tính góc giữa 2 mặt phẳng
Ví dụ 1. Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh bên bằng cạnh đáy và bằng \(2\sqrt{2}\). Gọi \(M,N\) lần lượt là trung điểm của \(SA\) và \(SC\). Tính côsin của góc giữa hai mặt phẳng \((BMN)\)và \((BDN)\)?
Hướng dẫn giải
Hình vẽ minh họa:
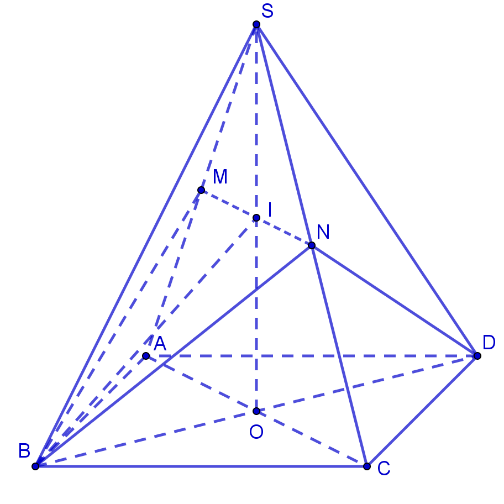
Gọi \(O = AC \cap BD\ ,\ \ I = SO \cap
MN\).
Ta có:
\(AC = 4,BN = 2\sqrt{2}.\frac{\sqrt{3}}{2}
= \sqrt{6},OI = \frac{1}{2}SO = \frac{1}{2}\sqrt{SC^{2} - OC^{2}} =
1\) và \(ON = \frac{1}{2}SA =
\sqrt{2}\).
Gọi \(H,K\) lần lượt là hình chiếu vuông góc của \(D\) lên \(BN,(BMN)\).
Khi đó: \(DH\bot BN,DK\bot(BMN) \Rightarrow
DK\bot BN\).
\(\left\{ \begin{matrix}
BN\bot DH \\
BN\bot DK
\end{matrix} \right.\ \Rightarrow BN\bot HK\).
Từ đó ta có: \(\left( (BMN),(BDN) \right) =
\widehat{DHK} = \varphi\).
Ta có: \(DH = \frac{2S_{BDN}}{BN} =
\frac{BD.NO}{BN} = \frac{4\sqrt{3}}{3}\) và \(DK = 2d\left\lbrack O;(BMN) \right\rbrack =
2\frac{OI.BO}{\sqrt{OI^{2} + BO^{2}}} = \frac{4}{\sqrt{5}}\)
Suy ra: \(\sin\varphi = \sin\left(
(BMN),(BDN) \right) = \sin\widehat{DHK} = \frac{DK}{DH} =
\frac{\sqrt{15}}{5}\)
\(\Rightarrow \cos\widehat{DHK} =
\frac{\sqrt{10}}{5}\).
Ví dụ 2. Cho hóp chóp đều \(S.ABCD\)có tất cả các cạnh bằng \(a\). Gọi \(M\ ,\
N\) lần lượt là trung điểm của \(SA\ ,\
SB\) và \(G\) là trọng tâm tam giác \(BCD.\) Gọi \(\alpha\) là góc giữa hai mặt phẳng \((GMN)\) và \((SBD)\). Tính giá trị của \(\sin\alpha\)?
Hướng dẫn giải
Hình vẽ minh họa:
Dựng đường cao \(SO\) của hình chóp.
Gọi \(K = SO \cap GM\).
Ta có: \((GMN) \cap (ABCD) = GE\) song song với \(CD\ ,\ \ E \in
OD\).
Khi đó: \(N,K,E\) thẳng hàng và \(NE = (BMN) \cap (SBD)\).
Ta có: \(\sin\alpha =
\frac{d(M,(SBD))}{d(M,NE)}\).
Dễ thấy tam giác \(BSD\) vuâng cân tại \(S\) nên \(SO = \frac{a\sqrt{2}}{2}\).
Chứng minh được: \(KS = 4KO \Rightarrow SK
= \frac{4}{5}SO = \frac{2a\sqrt{2}}{5}.\)
Trong tam giác \(KMN\) dựng hai đường cao \(KI,\ MJ.\)
Ta có: \(KN = \sqrt{SN^{2} + SK^{2} -
2SN.SK.cos45{^\circ}} = \frac{a\sqrt{17}}{10}\ \ ,\ \ MN =
\frac{a}{2}.\)
Do đó:
\(d(M,NE) = MJ = \frac{KI.MN}{KN} =
\frac{\sqrt{\frac{17a^{2}}{100} -
\frac{a^{2}}{16}}.\frac{a}{2}}{\frac{a\sqrt{17}}{10}} =
\frac{a\sqrt{43}}{4\sqrt{17}}\).
\(d(M,(SBD)) = \frac{d(A,(SBD))}{2} =
\frac{a\sqrt{2}}{4} \Rightarrow \sin\alpha =
\sqrt{\frac{34}{43}}.\)
C. Bài tập vận dụng có đáp án chi tiết
Bài tập 1. Cho khối chóp \(S.ABCD\) có đáy là hình bình hành, \(AB = 3,AD = 4,\
\widehat{BAD} = 120{^\circ}\), cạnh bên \(SA = 2\sqrt{3}\) và vuông góc với mặt đáy. Gọi \(M,\ \ N,\ \ P\) lần lượt là trung điểm các cạnh \(SA,\ \ AD,\ \ BC\). Tính góc giữa hai mặt phẳng \((SBC)\) và \((MNP)\).
Bài tập 2. Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 2a\ ,\ \ AD = a\ ,\ \ AA' =
a\sqrt{3}.\) Gọi \(\alpha\) là góc giữa hai mặt phẳng \((A'C'B)\) và \((A'C'D).\) Tính \(\sin\alpha.\)
Bài tập 3. Cho hình lăng trụ đứng \(ABC.A'B'C'\) có \(AB = a,\ AC = a\sqrt{3},\ \widehat{BAC} =
150{^\circ}\), \(AA' = a\). Gọi \(I\) là trung điểm của \(CC'\). Tính sin của góc giữa mặt phẳng \((AB'I)\) và mặt phẳng \((ABC)\).
Tài liệu còn dài, mời bạn đọc tải tài liệu tham khảo đầy đủ!
-----------------------------
Nắm vững cách tính góc giữa hai mặt phẳng thông qua việc dựng đường vuông góc đúng bản chất sẽ giúp người học tiếp cận hình học không gian một cách logic và chính xác hơn. Đây là nền tảng quan trọng để giải nhanh các bài toán góc trong không gian, đồng thời nâng cao khả năng tư duy và vận dụng trong các dạng toán nâng cao Toán 11.
