Ứng dụng khoảng cách tính góc giữa đường thẳng và mặt phẳng (Có lời giải)

Trong chương Góc và khoảng cách trong không gian, dạng toán tính góc giữa đường thẳng và mặt phẳng luôn được xem là nội dung trọng tâm, xuất hiện thường xuyên trong các đề kiểm tra và đề thi. Việc ứng dụng khoảng cách để xác định góc không chỉ giúp lời giải gọn gàng, logic mà còn nâng cao tư duy hình học không gian Toán 11.

A. Cách tính góc giữa đường thẳng và mặt phẳng qua khoảng cách

Trong không gian, cho đường thẳng \(d\) và mặt phẳng \((P)\) không vuông góc và không song song với nhau.

Gọi \(\varphi = \left( d,(P) \right)\). Ta biết rằng: \(\varphi = \left( d,(P) \right) = (d,d') = \widehat{AIH}\)

với \(d'\) là hình chiếu của \(d\) trên \((P)\), \(A \in d\) và \(A \notin (P)\), \(I = d \cap (P)\), \(H\) là hình chiếu của \(A\) trên \((P)\).

Từ đó ta có: \(\sin\varphi = \frac{AH}{AI} = \frac{d\left( A,\ (P) \right)}{AI}\).

Như vậy việc tính góc giữa đường thẳng \(d\) và mặt phẳng \((P)\) có thể quy về việc tính khoảng cách từ \(A\) tới \((P)\) và tính độ dài \(AI\).

B. Bài tập minh họa tính góc giữa đường thẳng và mặt phẳng trong không gian

Hướng dẫn giải

Hình vẽ minh họa:

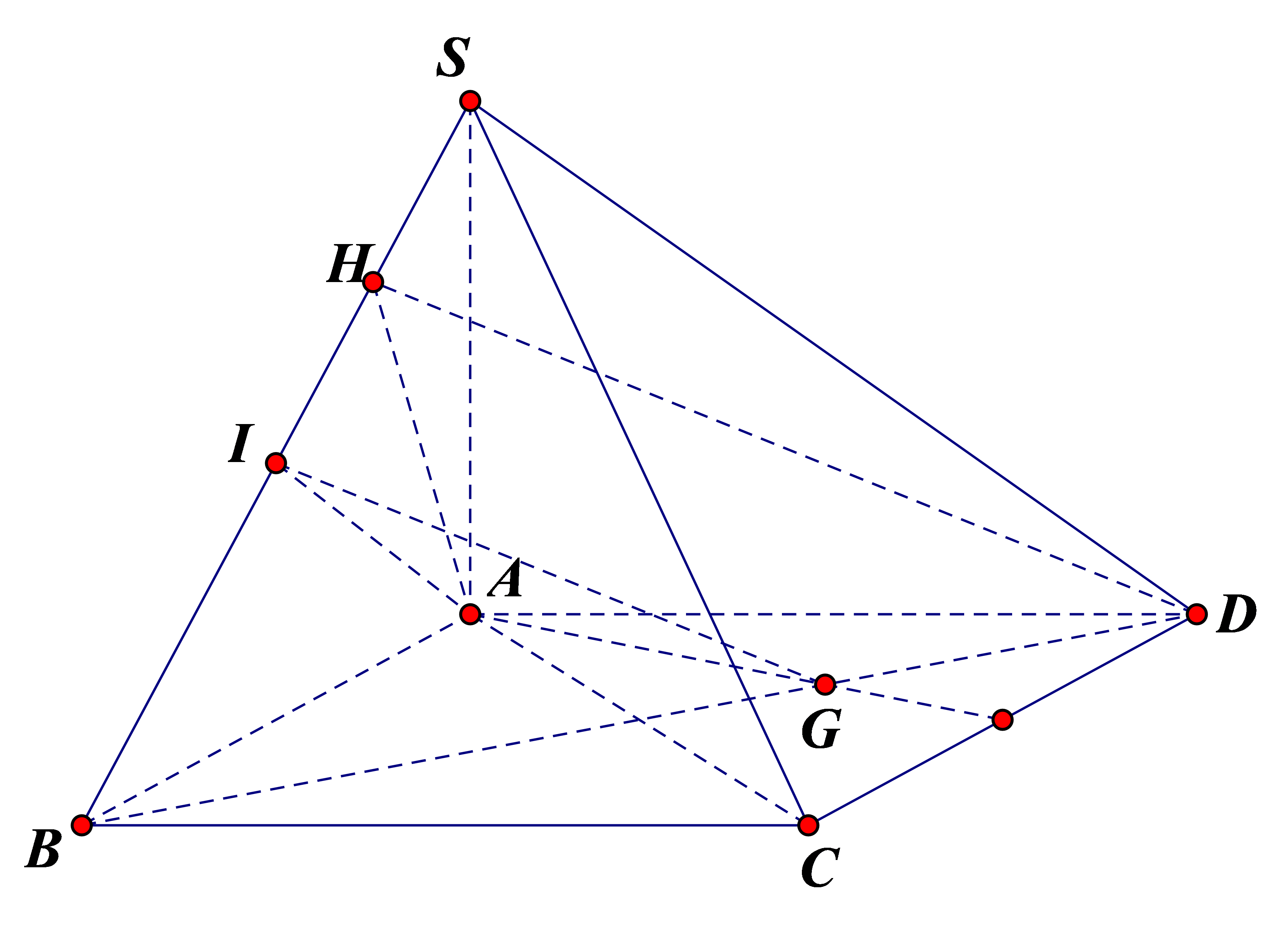
Ta có \(SB = 2a\) nên suy ra được tam giác \(SAI\) đều cạnh \(a\).

Gọi \(H\) là trung điểm của \(SI\) thì \(\frac{BI}{BH} = \frac{BG}{BD}\) nên \(IG//HD\).

Do đó \(\left( IG,(SCD) \right) = \left( HD,(SCD) \right)\).

Xét tam giác tam giác vuông \(AHD\) có \(AH = \frac{a\sqrt{3}}{2}\), \(AD = \frac{3a}{2}\) suy ra \(HD = a\sqrt{3}\).

Vì \(HS = \frac{1}{4}BS\) nên \(d\left( H,(SCD) \right) = \frac{1}{4}d\left( B,(SCD) \right) = \frac{1}{4}d\left( A,(SCD) \right) = \frac{1}{4}d\)

Mà \(\frac{1}{d^{2}} = \frac{1}{SA^{2}} + \frac{1}{AD^{2}} = \frac{1}{a^{2}} + \frac{4}{9a^{2}} = \frac{13}{9a^{2}}\)

\(\Rightarrow d = \frac{3a}{\sqrt{13}}\) \(\Rightarrow d\left( H,(SCD) \right) = \frac{3a}{4\sqrt{13}}\).

Suy ra

\(\sin\left( HD,(SCD) \right) = \frac{d\left( H,(SCD) \right)}{HD} = \frac{3a}{4\sqrt{13}.a\sqrt{3}} = \frac{\sqrt{3}}{4\sqrt{13}}\).

Hướng dẫn giải

Hình vẽ minh họa:

Gọi \(\varphi\) là góc tạo bởi đường thẳng \(ID\) và mặt phẳng \((ICB)\), \(H\) là trọng tâm tam giác \((ACD)\).

Ta có:

\(\sin\varphi = \frac{d\left( D;\ (ICB) \right)}{ID} = \frac{3}{2}.\frac{d\left( H;\ (ICB) \right)}{ID}\).

Gọi \(E\) là hình chiếu của \(H\) lên \(CB\), \(K\) là hình chiếu của \(H\) lên \(IE\), ta chứng minh được \(d\left( H;(ICB) \right) = HK\).

Ta có: \(HE = \frac{2}{3}DC =\frac{2a}{3};\ D'I = \frac{1}{3}D'B' =\frac{1}{3}\sqrt{4\ a^{2} + a^{2}} = \frac{a\sqrt{5}}{3}\).

Mà \(A'A = \sqrt{A'B^{2} - AB^{2}} = \sqrt{3a^{2} - a^{2}} = a\sqrt{2} \Rightarrow HI = a\sqrt{2}\).

\(DI = \sqrt{D{D'}^{2} + D'I^{2}} = \sqrt{2\ a^{2} + \frac{5\ a^{2}}{9}} = \frac{a\sqrt{23}}{3}\)

\(\Rightarrow d\left( H;(ICB) \right) = HK= \frac{HE.HI}{\sqrt{HE^{2} + HI^{2}}}\)

\(=\frac{\frac{2a}{3}.a\sqrt{2}}{\sqrt{\frac{22\ a^{2}}{9}}} =\frac{2a}{\sqrt{11}} \Rightarrow \sin\varphi =\frac{9}{\sqrt{253}}\).

Hướng dẫn giải

Hình vẽ minh họa:

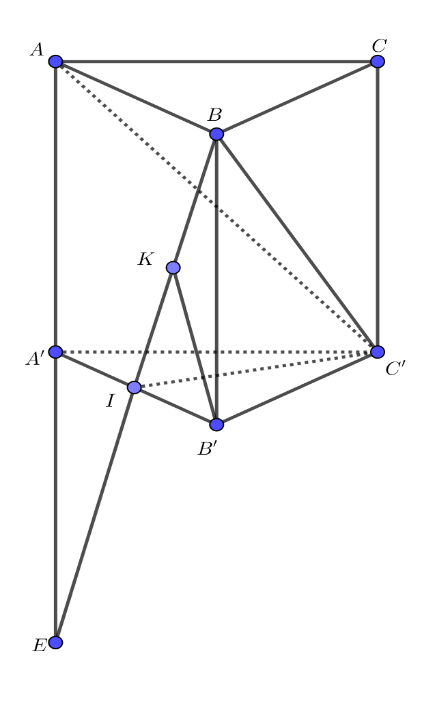
Gọi \(K\) là trung điểm \(IB\), \(\varphi\) là góc giữa \(AC'\) và \((BIC')\).

Ta có: \(\sin\varphi = \frac{d\left( A,(BIC') \right)}{AC'}\)

Ta có: \(\left\{ \begin{matrix} (BIC')\bot(ABB'A')\ \ \ \ \left( do\ \ C'I\bot(ABB'A') \right) \\ (BIC') \cap (ABB'A') = IB \\ B'K\bot IB \end{matrix} \right.\) \(\Rightarrow B'K\bot(BIC')\).

Mặt khác \(I\) là trung điểm \(A'B'\) nên \(d\left( A',(BIC') \right) = d\left( B',(BIC') \right) = B'K\)

Gọi \(E\) là giao điểm của \(A'A\) và \(BI\), ta có \(\frac{EA'}{EA} = \frac{d\left( A',(BIC') \right)}{d\left( A,(BIC') \right)}\)

Mặt khác \(\frac{EA'}{EA} = \frac{A'I}{AB} = \frac{1}{2}\ \ (do\ AB\ \ //\ A'I)\)

Suy ra \(\frac{EA'}{EA} = \frac{d\left(A',(BIC') \right)}{d\left( A,(BIC') \right)} = \frac{1}{2}\)\(\Leftrightarrow d\left( A,(BIC') \right) = 2d\left(A',(BIC') \right) = 2B'K = 2.\frac{a\sqrt{2}}{2} =a\sqrt{2}\)

\(AC' = \sqrt{A'A^{2} + A'{C'}^{2}} = a\sqrt{5}\)

\(\Rightarrow \sin\varphi = \frac{d\left( A,(BIC') \right)}{AC'} = \frac{a\sqrt{2}}{a\sqrt{5}} = \frac{\sqrt{10}}{5} \Rightarrow \cos\varphi = \frac{\sqrt{15}}{5}\).

C. Bài tập vận dụng có đáp án chi tiết

Bài tập 1. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, \(AB = 2a\), \(BC = a\), \(\widehat{ABC} = 120{^\circ}\), cạnh bên \(SD = a\sqrt{3}\), \(SD\bot(ABCD)\). Gọi \(\varphi\) là góc giữa đường thẳng \(SB\) và mặt phẳng \((SAC)\), tính \(sin\varphi\).

Bài tập 2. Cho hình chóp đều \(S.ABCD\) có \(SA = AB = a\). Gọi \(M\)là trung điểm của cạnh \(BC\). Tính tan của góc giữa đường thẳng \(DM\) và mặt phẳng \((SAB)\).

Bài tập 3. Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\),\(SO = \frac{a}{2}\) với \(O\) là tâm của đáy. Gọi \(E\) là trung điểm cạnh \(AD\), \(\varphi\) là góc giữa đường thẳng \(CD\) và mặt phẳng \((SBE)\). Tính \(\sin\varphi\).

Bài tập 4. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\), \(\widehat{ABC} = 60{^\circ}\) và \(SB = a\). Hình chiếu vuông góc của điểm \(S\) lên mặt phẳng \((ABC)\) trùng với trọng tâm của tam giác \(ABC\). Gọi \(\varphi\) là góc giữa đường thẳng \(SB\) và mặt phẳng \((SCD)\). Tính \(\sin\varphi\).

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!

------------------------------------

Thông qua việc ứng dụng khoảng cách trong tính toán góc giữa đường thẳng và mặt phẳng, người học có thể tiếp cận bài toán không gian một cách khoa học, chính xác và hiệu quả hơn. Nắm vững phương pháp này sẽ giúp xử lý nhanh các bài toán góc và khoảng cách trong không gian, đồng thời tạo nền tảng vững chắc cho những dạng toán nâng cao và các kỳ thi quan trọng.