Đề thi học kì 2 môn Toán lớp 12 năm 2018 Sở GD&ĐT Quảng Nam
Đề thi học kì 2 môn Toán 12
Trang 1/3 – Mã đề 101
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2017-2018
Môn: TOÁN – Lớp 12
Thời gian làm bài: 60 phút, không kể thời gian phát đề
Mã đề 101
Họ và tên học sinh: ……………………………..……………….
Số báo danh: ……………………………………..……………..
Câu 1. Tìm họ nguyên hàm của hàm số
5
( ) 2.f x x
A.
5 6
1
( 2)d 2 .
6
x x x x C
B.
5 6
1
( 2)d .
6
x x x C
C.
5 4
( 2)d 5 2 .x x x x C
D.
5 4
( 2)d 5 .x x x C
Câu 2. Tìm
2
1
d .
cos
x
x
A.
2
1
d tan .
cos
x x C
x
B.
2
1
d tan .
cos
x x C
x
C.
2
1
d cot .
cos
x x C
x
D.
2
1
d cot .
cos
x x C
x
Câu 3. Cho
( )f x
là hàm số bất kỳ liên tục trên
và
, ,a b c
là ba số thực tùy ý. Mệnh đề nào sau đây
sai ?
A.
d d d .
c b c
a a b
f x x f x x f x x
B.
d d d .
b c c
a a b
f x x f x x f x x
C.
d d d .
c b b
a a c
f x x f x x f x x
D.
d d .
b b
a a
cf x x c f x x
Câu 4. Cho
1 1
0 0
2 ( ) d 3, d 1.f x g x x f x x
Tính
1
0
d .I g x x
A.
1.I
B.
1.I
C.
2.I
D.
2.I
Câu 5. Cho hàm số
( )y f x
có đạo hàm liên tục trên đoạn
[1;2], (1) 3, (2) 1.f f
Tính tích phân
2
1
' d .I f x x
A.
2.I
B.
2.I
C.
4.I
D.
4.I
Câu 6. Phần thực; phần ảo của số phức
3 4z i
theo thứ tự bằng
A.
3; 4.
B.
3; 4.
C.
4; 3.
D.
4; 3.
Câu 7. Số phức liên hợp của số phức
7 4z i
là
A.
4 7 .z i
B.
7 4 .z i
C.
7 4 .z i
D.
7 4 .z i
Câu 8. Điểm nào dưới đây là điểm biểu diễn số phức
1 2z i
trên mặt phẳng tọa độ ?
A.
( 2;1).M
B.
(1; 2).N
C.
(2;1).P
D.
(1;2).Q
Câu 9. Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
với
(2; 1;0)A
,
(1;0;4)B
,
(0; 2;2)C
. Tìm tọa độ trọng tâm
G
của tam giác
ABC
.
A.
(1; 1;2)G
. B.
(3; 3;6)G
. C.
3 3
; ;2
2 2
G
. D.
1 1 2
; ;
3 3 3
G
.
Câu 10. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
(3;2; 4)M
. Điểm nào dưới đây là hình chiếu
vuông góc của điểm
M
trên mặt phẳng
( )Oyz
?
A.
1
(0;2;0)H
. B.
2
(0;0; 4)H
. C.
3
(3;0;0)H
. D.
4
(0;2; 4)H
.
Câu 11. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
(1;2;2)u
,
( 3;1;0)v
. Tìm tọa độ
của vectơ
2a u v
.
A.
( 1;3;4)a
. B.
(5;3;4)a
. C.
(4;1;2)a
. D.
( 1;5;4)a
.
Trang 2/3 – Mã đề 101
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 0.P x z
Mặt phẳng
( )P
có
một vectơ pháp tuyến là
A.
1
(2;0; 1)n
. B.
2
(2; 1; 2)n
. C.
3
(2; 1;0)n
. D.
4
(2;0; 2)n
.
Câu 13. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
2 1 1
: .
1 1 2
x y z
d
Mặt phẳng đi
qua gốc tọa độ và vuông góc với đường thẳng
d
có phương trình là
A.
2 0.x y z
B.
2 0.x y z
C.
2 0.x y z
D.
0.x y z
Câu 14. Biết
( )F x
là một nguyên hàm của hàm số
1
( )
2 1
f x
x
và
1 1F
. Tính
5F
.
A.
241
5 .
81
F
B.
5 1 2ln3.F
C.
1
5 ln3.
2
F
D.
5 1 ln 3.F
Câu 15. Tìm
cos
sin . d .
x
x e x
A.
cos sin
sin . d cos . .
x x
x e x x e C
B.
cos sin
sin . d cos . .
x x
x e x x e C
C.
cos cos
sin . d .
x x
x e x e C
D.
cos cos
sin . d .
x x
x e x e C
Câu 16. Tìm họ nguyên hàm của hàm số
2
1
( )
4
f x
x
.
A.
2
1 2
d ln .
2
4
x
x C
x
x
B.
2
1 2
d ln .
2
4
x
x C
x
x
C.
2
1 1 2
d ln .
4 2
4
x
x C
x
x
D.
2
1 1 2
d ln .
4 2
4
x
x C
x
x
Câu 17. Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị
2
( ): 2C y x x
, trục hoành và hai đường
thẳng
1, 3.x x
A.
2.S
B.
2
.
3
S
C.
4.S
D.
8
.
3
S
Câu 18. Gọi
1 2
,z z
là hai nghiệm phức của phương trình
2
3 9 0z z
, trong đó
1
z
có phần ảo dương.
Phần thực của số phức
1 2
2017 2018w z z
bằng
A.
3.
B.
3.
C.
3
.
2
D.
3
.
2
Câu 19. Cho số phức
z
thỏa mãn
3 1 5iz z i
. Môđun của
z
bằng
A.
5.
B.
5 2
.
4
C.
65
.
4
D.
65
.
5
Câu 20. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
3 2
: 2
x t
d y t
z t
. Điểm nào dưới đây
không thuộc
d
?
A.
(5;1;1)M
. B.
( 1; 4; 2)N
. C.
(1;3; 1)P
. D.
(7;0;2)Q
.
Câu 21. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 3 2
: .
2 1 1
x y z
d
Gọi
( ; ; ) (c 0)M a b c
là điểm thuộc đường thẳng
d
sao cho khoảng cách từ
M
đến mặt phẳng
( )Oxy
bằng 1.
Tính
a b c
.
A.
0.a b c
B.
4.a b c
C.
6.a b c
D.
10.a b c
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, cho hai đường thẳng
1
1 1
: ;
1 2 2
x y z
d
2
3
: 1
2
x t
d y
z t
.
Tính số đo góc
giữa hai đường thẳng
1 2
,d d
.
A.
0
60
. B.
0
90
. C.
0
45
. D.
0
30
.
Trang 3/3 – Mã đề 101
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
(1;1;1)A
,
(2; 1;3)B
và song song với đường thẳng
1
: 0
2
x t
d y
z t
. Gọi
( ; ; )n a b c
là một vectơ pháp tuyến của
của mặt phẳng
( )P
. Tính
a b
c
.
A.
1
2
a b
c
. B.
1
2
a b
c
. C.
2
a b
c
. D.
2
a b
c
.
Câu 24. Biết
5
2
1
ln
d .ln5
x
x a b
x
với
,a b
là các số hữu tỉ. Tính tích
.a b
.
A.
4
.
25
ab
B.
4
.
25
ab
C.
6
.
25
ab
D.
6
.
25
ab
Câu 25. Cho hình phẳng
( )H
giới hạn bởi parabol
2
( ) :P y x
, trục hoành và tiếp tuyến của
( )P
tại
điểm
(2;4)M
. Tính thể tích
V
của khối tròn xoay tạo thành khi quay hình
( )H
xung quanh trục hoành.
A.
176
.
15
V
B.
16
.
15
V
C.
77
.
15
V
D.
64
.
15
V
Câu 26. Có bao nhiêu số phức
z
thỏa mãn
2 2z i
và
2
z
là số thuần ảo ?
A. 1. B. 2. C. 3. D. 4.
Câu 27. Cho số phức
z
có môđun bằng 8. Biết rằng tập hợp điểm trong mặt phẳng tọa độ biểu diễn các
số phức
2 4 3w z i
là đường tròn có tâm
( ; )I a b
, bán kính
R
. Tổng
a b R
bằng
A. 7. B. 9 C. 15. D. 17.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( )S
có tâm
(2;1; 2)I
và cắt trục
'y Oy
tại
hai điểm
,A B
sao cho tam giác
IAB
vuông. Phương trình của mặt cầu
( )S
là
A.
2 2 2
( 2) ( 1) ( 2) 2x y z
. B.
2 2 2
( 2) ( 1) ( 2) 4x y z
.
C.
2 2 2
( 2) ( 1) ( 2) 8x y z
. D.
2 2 2
( 2) ( 1) ( 2) 16x y z
.
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
(1; 2;0), ( 3;2; 4)A B
và mặt phẳng
( ) : 2 3 0.P x y z
Gọi
( ; ; )M a b c
là điểm thuộc mặt phẳng
( )P
sao cho tam giác
MAB
cân tại
M
và có diện tích nhỏ nhất. Tính
. .a b c
.
A.
. . 2a b c
. B.
. . 1a b c
. C.
. . 0a b c
. D.
. . 2a b c
.
Câu 30. Cho hàm số
( )y f x
liên tục trên đoạn
0;
3
. Biết
'( ).cos ( ).sin 1, 0;
3
f x x f x x x
và
(0) 1f
. Tính tích phân
3
0
d .I f x x
A.
3 1
.
2
I
B.
3 1
.
2
I
C.
1
.
2
I
D.
1
.
2 3
I
Câu 31. Cho số phức
z
có môđun lớn nhất thỏa mãn
2
4 .5iz z
Tính
.z z
.
A.
. 9.z z
B.
. 16.z z
C.
. 25.z z
D.
. 41.z z
Câu 32. Cho hình lập phương
. ' ' ' 'ABCD A B C D
có cạnh bằng 1. Gọi
,M N
theo thứ tự là hai điểm thay
đổi trên hai cạnh
,AB AD
sao cho
AM DN
(
M
không trùng với
,A B
). Biết rằng tồn tại một mặt cầu
cố định có tâm thuộc đường thẳng
'AC
và tiếp xúc với mặt phẳng
( ' )A MN
khi
,M N
thay đổi. Tính
bán kính
R
của mặt cầu đó.
A.
3
2
R
. B.
1
2
R
. C.
2
2
R
. D.
1R
.
--------------- HẾT ---------------
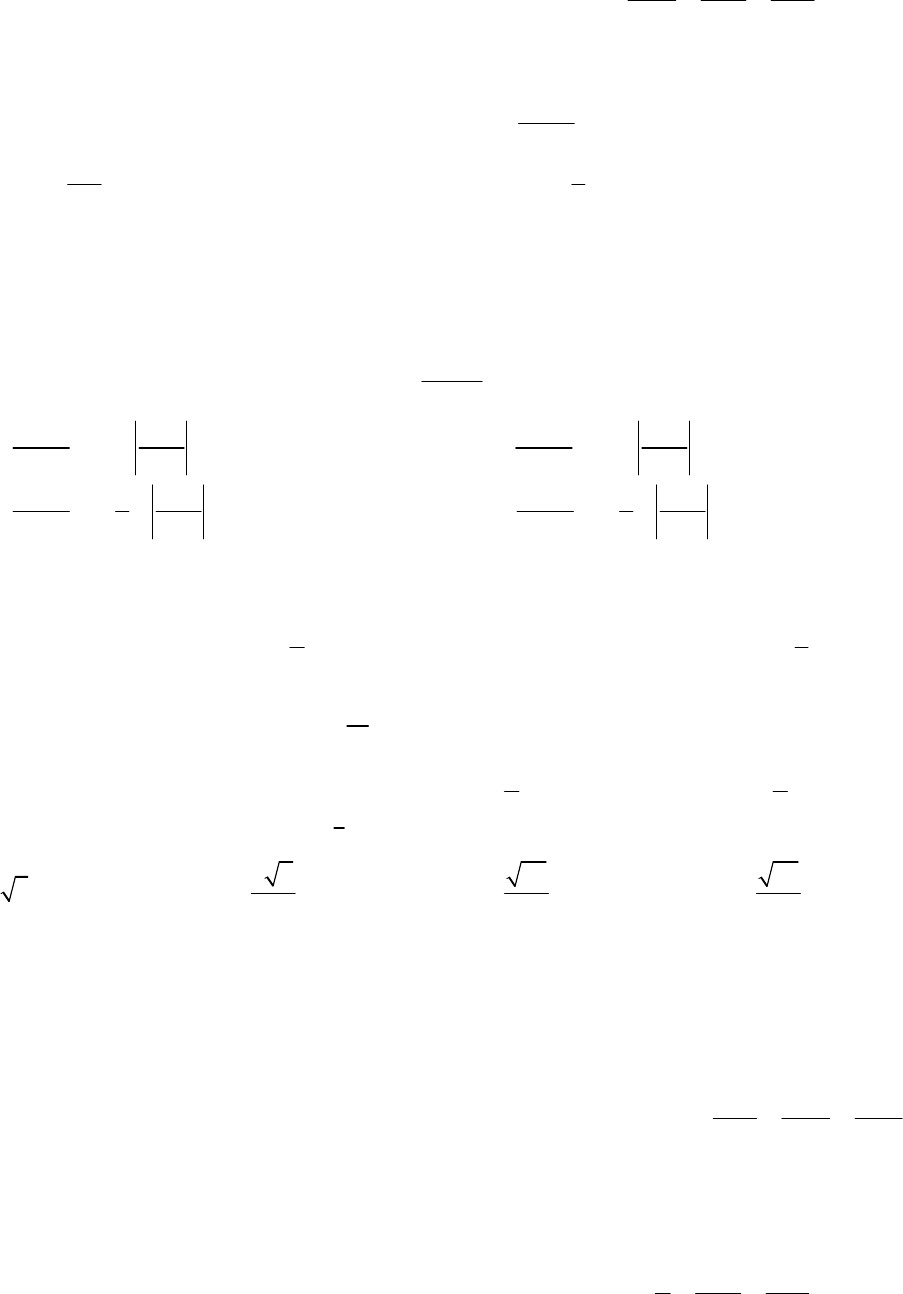
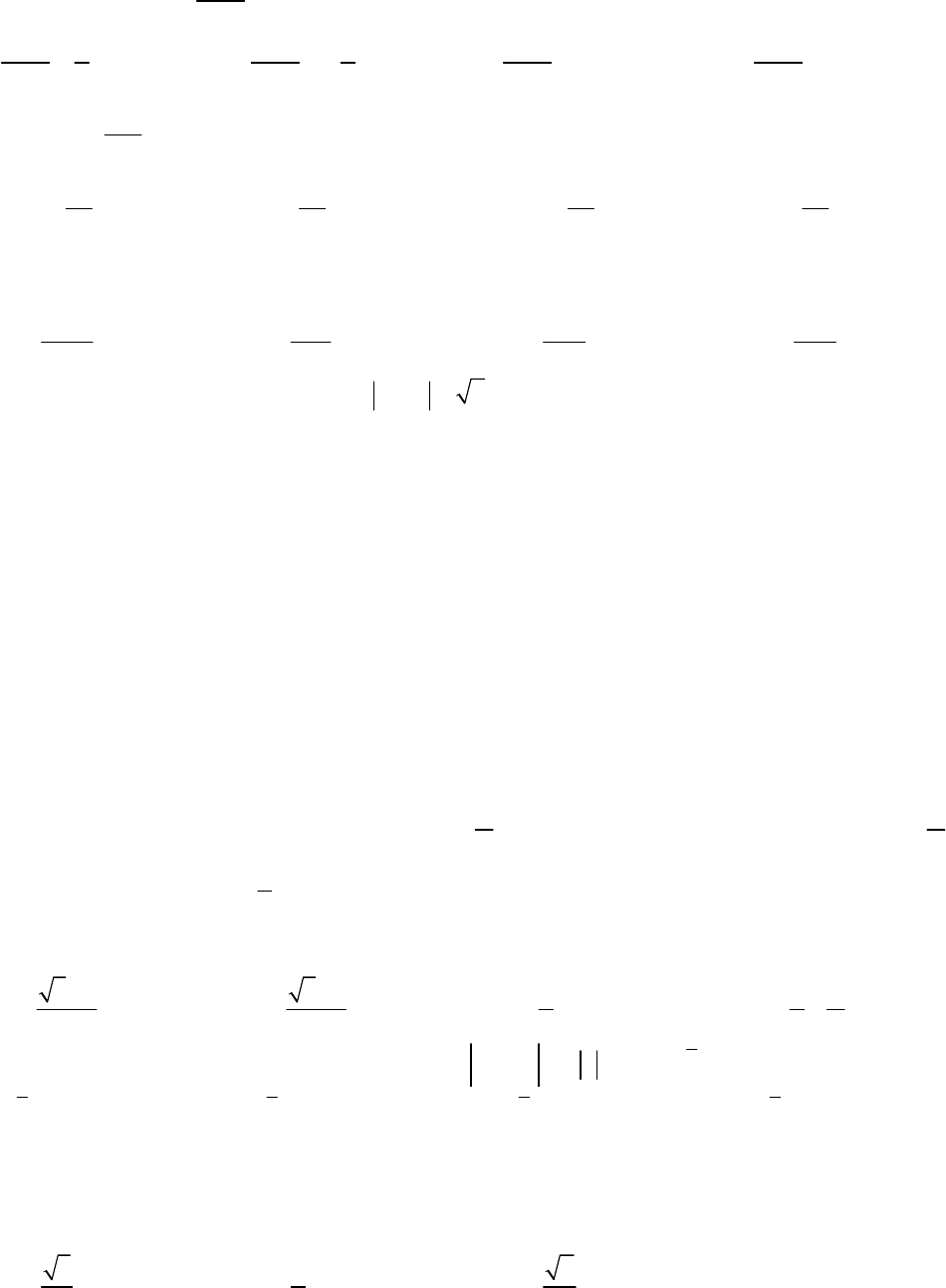
Đề thi học kì 2 môn Toán lớp 12 năm 2018
VnDoc xin giới thiệu tới bạn đọc tài liệu Đề thi học kì 2 môn Toán lớp 12 năm 2018 Sở GD&ĐT Quảng Nam, nội dung tài liệu kèm theo đáp án sẽ là nguồn thông tin hay để phục vụ công việc học tập của các bạn học sinh được tốt hơn. Mời thầy cô và các bạn học sinh cùng tham khảo.
Đề thi học kì 2 môn Toán lớp 12 năm 2017 - 2018 Sở GD&ĐT Bến Tre
Đề thi học kì 2 môn Toán lớp 12 năm 2017 - 2018 trường THPT Tân Hiệp - Kiên Giang
Đề thi học kì 2 môn Toán lớp 12 năm 2017 - 2018 trường THPT Ngô Quyền - Quảng Ninh
Đề thi học kì 2 môn Toán lớp 12 năm học 2017 - 2018 trường THPT Duyên Hải - Trà Vinh
---------------------------------------------
Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Đề thi học kì 2 môn Toán lớp 12 năm 2018 Sở GD&ĐT Quảng Nam. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Thi thpt Quốc gia môn Toán, Thi thpt Quốc gia môn Hóa học, Thi thpt Quốc gia môn Vật Lý, Thi thpt Quốc gia môn Sinh học mà VnDoc tổng hợp và đăng tải.
