Đề thi thử THPT Quốc gia môn Toán năm 2016 tỉnh Thanh Hóa (Lần 1)

Đề thi thử THPT Quốc gia môn Toán 2016 tỉnh Thanh Hóa

Đề thi thử THPT Quốc gia môn Toán năm 2016 tỉnh Thanh Hóa (Lần 1) gồm 10 câu hỏi có đáp án đi kèm, được VnDoc.com sưu tầm và đăng tải. Đây là đề luyện thi THPT Quốc gia, ôn thi Đại học, Cao đẳng hữu ích dành cho các bạn thí sinh, giúp các bạn củng cố và nâng cao kỹ năng làm bài môn Toán. Mời các bạn tham khảo.

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Lê Lợi, Thanh Hóa

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Nguyễn Huệ, Hà Nội

Câu 1 (1,5 điểm). Cho hàm số

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.

b) Viết phương trình tiếp tuyến của (C) tại điểm A là giao điểm của (C) với trục hoành.

Câu 2 (0,5 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x⁴ - 2x² + 3 trên đoạn [0;4]

Câu 3 (1,0 điểm).

a) Giải phương trình z² - z + 1 trên tập số phức.

b) Giải bất phương trình log₂(x - 3) + log₂(x - 1) ≤ 3.

Câu 4 (1,0 điểm). Tính tích phân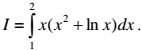

Câu 5 (1,0 điểm). Trong không gian với hệ tọa độ Oxy, cho ba điểm A(5;-2;3), B(1;2;3), C(1;-2;1). Viết phương trình mặt phẳng (P) đi qua ba điểm A, B, C và viết phương trình mặt cầu (S) có tâm I(2;-1;3) và tiếp xúc với mặt phẳng (P).

Câu 6 (1,0 điểm).

a) Tính giá trị của biểu thức A = sin3α + sin²2α, biết 2cos2α + 7sin2α = 0.

b) Trong kì thi THPT quốc gia, tại hội đồng thi X, trường THPT A có 5 thí sinh dự thi. Tính xác suất để có đúng 3 thí sinh của trường THPT A được xếp vào cùng một phòng thi, biết rằng hội đồng thi X gồm 10 phòng thi, mỗi phòng thi có nhiều hơn 5 thí sinh và việc xếp các thí sinh vào các phòng thi là hoàn toàn ngẫu nhiên.

Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AD là đáy lớn, AD = 2a, AB = BC = CD = a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H thuộc đoạn thẳng AC sao cho HC = 2HA. Góc giữa hai mặt phẳng (SCD) và (ABCD) bằng 60^o khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SA và CD.

Câu 8 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình bình hành ABCD có tâm I(2√3 - 2;5) BC = 2AB, góc BAD = 60^o, Điểm đối xứng với A qua B là E(-2;9). Tìm tọa độ các đỉnh của hình bình hành ABCD biết rằng A có hoành độ âm.

Câu 9 (1,0 điểm). Giải bất phương trình

Câu 10 (1,0 điểm). Cho a, b, c là độ dài ba cạnh của một tam giác. Tìm giá trị lớn nhất của biểu thức:

Đáp án đề thi thử THPT Quốc gia 2016 môn Toán

Câu 1:

1) Hàm số có TXĐ: D = R \ {1}

2) Sự biến thiên của hàm số:

a) Giới hạn vô cực và các đường tiệm cận:

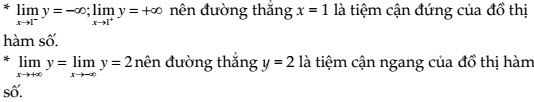
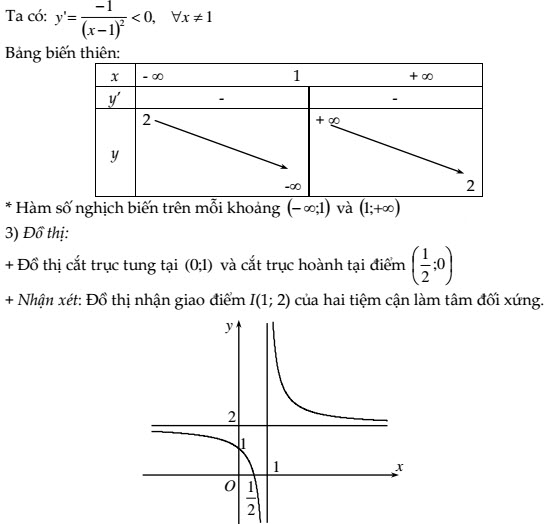
b) Bảng biến thiên:

(Còn tiếp)