VnDoc.com

Tìm m để bất phương trình logarit có nghiệm trên tập D

Giải bất phương trình logarit chứa tham số

Bài trước

Tải về

Bài sau

Lớp: Lớp 11

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại: Tài liệu Lẻ

Mức độ: Khó

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Tìm m để bất phương trình logarit có nghiệm

A. Cách tìm m để BPT logarit có nghiệm trên tập xác định
B. Bài tập minh họa tìm tham số để BPT logarit có nghiệm trên tập xác định
C. Bài tập tự rèn luyện có đáp án chi tiết

Trong chuyên đề bất phương trình logarit chứa tham số, dạng toán tìm m để bất phương trình logarit có nghiệm trên tập D là dạng bài tiêu biểu giúp học sinh rèn luyện tư duy đại số và kỹ năng xử lý điều kiện logarit. Bài viết này sẽ hướng dẫn bạn cách xác định điều kiện xác định của logarit, thiết lập và tìm giá trị m phù hợp, đồng thời cung cấp ví dụ minh họa chi tiết, lời giải có phân tích để bạn dễ hiểu và dễ áp dụng trong quá trình ôn luyện thi THPT Quốc gia.

A. Cách tìm m để BPT logarit có nghiệm trên tập xác định

Phương pháp giải:

Bước 1. Tách tham số $m$ ra khỏi $x$ và đưa BPT về dạng $A(m) \leq f(x)$ $A(m) \leq f(x)$ hoặc $A(m) \geq f(x)$ $A(m) \geq f(x)$.
Bước 2. Khảo sát sự biến thiên và dựa vào bảng biến thiên xác định các giá trị của tham số $m$ để bất phương trình có nghiệm.

Chú ý: Cho hàm số $y = f(x)$ xác định và liên tục trên $D$.

Trong trường hợp tồn tại $\max_{x \in D}f(x)$ $\max_{x \in D}f(x)$ và $\min_{x \in D}f(x)$ $\min_{x \in D}f(x)$ thì ta có:

Bất phương trình $A(m) \leq f(x)$ $A(m) \leq f(x)$ có nghiệm trên $D \Leftrightarrow A(m) \leq \max_{x \in D}f(x)$ $D \Leftrightarrow A(m) \leq \max_{x \in D}f(x)$.
Bất phương trình $A(m) \geq f(x)$ $A(m) \geq f(x)$ có nghiệm trên $D \Leftrightarrow A(m) \geq \min_{x \in D}f(x)$ $D \Leftrightarrow A(m) \geq \min_{x \in D}f(x)$.

B. Bài tập minh họa tìm tham số để BPT logarit có nghiệm trên tập xác định

Ví dụ 1. Tìm $m$ để bất phương trình $\log_{2}^{2}2x - 2(m + 1)\log_{2}x - 2< 0$ $\log_{2}^{2}2x - 2(m + 1)\log_{2}x - 2< 0$ có nghiệm $x \in (\sqrt{2}; + \infty).$ $x \in (\sqrt{2}; + \infty).$

Hướng dẫn giải

Ta có:

$\log_{2}^{2}2x - 2(m + 1)\log_{2}x - 2 <0$ $\log_{2}^{2}2x - 2(m + 1)\log_{2}x - 2 <0$

$\Leftrightarrow \left( 1 + \log_{2}x\right)^{2} - 2(m + 1)\log_{2}x - 2 < 0$ $\Leftrightarrow \left( 1 + \log_{2}x\right)^{2} - 2(m + 1)\log_{2}x - 2 < 0$. $(*)$

Đặt $t = \log_{2}x$ $t = \log_{2}x$. Do $x \in (\sqrt{2}; + \infty) \Rightarrow t \in \left( \frac{1}{2}; + \infty \right)$ $x \in (\sqrt{2}; + \infty) \Rightarrow t \in \left( \frac{1}{2}; + \infty \right)$.

Khi đó $(*)$ trở thành $(1 + t)^{2} - 2(m + 1)t - 2 < 0$ $(1 + t)^{2} - 2(m + 1)t - 2 < 0$

$\Leftrightarrow \frac{(1 + t)^{2} - 2}{2t} - 1 < m$ $\Leftrightarrow \frac{(1 + t)^{2} - 2}{2t} - 1 < m$ $\Leftrightarrow f(t) = \frac{t^{2} - 1}{2t} < m$ $\Leftrightarrow f(t) = \frac{t^{2} - 1}{2t} < m$ (1).

Xét hàm $f(t) = \frac{t}{2} - \frac{1}{2t}$ $f(t) = \frac{t}{2} - \frac{1}{2t}$ liên tục trên $\left\lbrack \frac{1}{2}; + \infty \right)$ $\left\lbrack \frac{1}{2}; + \infty \right)$.

Ta có:

$f'(t) = \frac{1}{2} + \frac{1}{2t^{2}} > 0,\forall t \in \left( \frac{1}{2}; + \infty \right)$

$\Rightarrow \min_{\left\lbrack \frac{1}{2}; + \infty \right)}f(t) = f\left( \frac{1}{2} \right) = - \frac{3}{4}$ $\Rightarrow \min_{\left\lbrack \frac{1}{2}; + \infty \right)}f(t) = f\left( \frac{1}{2} \right) = - \frac{3}{4}$.

Khi đó (1) đúng với mọi $t \in \left( \frac{1}{2}; + \infty \right)$ $t \in \left( \frac{1}{2}; + \infty \right)$ khi $\min_{\left\lbrack \frac{1}{2}; + \infty \right)}f(t) < m$ $\min_{\left\lbrack \frac{1}{2}; + \infty \right)}f(t) < m$ $\Leftrightarrow m > - \frac{3}{4}$ $\Leftrightarrow m > - \frac{3}{4}$.

Ví dụ 2. Có tất cả bao nhiêu giá trị nguyên thuộc $( - 10;10)$ của tham số $m$ để bất phương trình $3\sqrt{x} + \sqrt{x + 4} < 2m\log_{4 - \sqrt{4 -x}}2$ $3\sqrt{x} + \sqrt{x + 4} < 2m\log_{4 - \sqrt{4 -x}}2$ có nghiệm?

Hướng dẫn giải

Điều kiện xác định: $\left\{ \begin{matrix} x \geq 0 \\ x \leq 4 \\ 4 - \sqrt{4 - x} \neq 1 \\ 4 - \sqrt{4 - x} > 0 \end{matrix} \right.\ \Leftrightarrow 0 \leq x \leq 4$ $\left\{ \begin{matrix} x \geq 0 \\ x \leq 4 \\ 4 - \sqrt{4 - x} \neq 1 \\ 4 - \sqrt{4 - x} > 0 \end{matrix} \right.\ \Leftrightarrow 0 \leq x \leq 4$.

Ta thấy $0 \leq x \leq 4 \Leftrightarrow 0 \leq 4 - x \leq 4 \Leftrightarrow 2 \leq 4 - \sqrt{4 - x} \leq 4$ $0 \leq x \leq 4 \Leftrightarrow 0 \leq 4 - x \leq 4 \Leftrightarrow 2 \leq 4 - \sqrt{4 - x} \leq 4$.

Suy ra $log_{4 - \sqrt{4 - x}}2 > 0$ $log_{4 - \sqrt{4 - x}}2 > 0$.

Khi đó bất phương trình:

$3\sqrt{x} + \sqrt{x + 4} < 2m\log_{4 -\sqrt{4 - x}}2$ $3\sqrt{x} + \sqrt{x + 4} < 2m\log_{4 -\sqrt{4 - x}}2$

$\Leftrightarrow m > \frac{3\sqrt{x} + \sqrt{x +4}}{2.\log_{4 - \sqrt{4 - x}}2}$ $\Leftrightarrow m > \frac{3\sqrt{x} + \sqrt{x +4}}{2.\log_{4 - \sqrt{4 - x}}2}$

$\Leftrightarrow m > \frac{1}{2}\left(3\sqrt{x} + \sqrt{x + 4} \right).\log_{2}\left( 4 - \sqrt{4 - x}\right)$ $\Leftrightarrow m > \frac{1}{2}\left(3\sqrt{x} + \sqrt{x + 4} \right).\log_{2}\left( 4 - \sqrt{4 - x}\right)$.

Xét hàm $f(x) = \frac{1}{2}\left(3\sqrt{x} + \sqrt{x + 4} \right).\log_{2}\left( 4 - \sqrt{4 - x}\right)$ $f(x) = \frac{1}{2}\left(3\sqrt{x} + \sqrt{x + 4} \right).\log_{2}\left( 4 - \sqrt{4 - x}\right)$ liên tục trên $\lbrack 0;4\rbrack$ $\lbrack 0;4\rbrack$.

Ta có:

$f'(x) = \frac{1}{2}\left(\frac{3}{2\sqrt{x}} + \frac{1}{2\sqrt{x + 4}} \right).\log_{2}\left( 4 -\sqrt{4 - x} \right)$ $+ \frac{1}{2}\left( 3\sqrt{x} + \sqrt{x + 4}\right).\frac{1}{2\sqrt{4 - x}.\left( 4 - \sqrt{4 - x} \right).\ln2} >0;\forall x \in (0;4)$ $+ \frac{1}{2}\left( 3\sqrt{x} + \sqrt{x + 4}\right).\frac{1}{2\sqrt{4 - x}.\left( 4 - \sqrt{4 - x} \right).\ln2} >0;\forall x \in (0;4)$

Suy ra hàm số $y = f(x)$ đồng biến trên $\lbrack 0;4\rbrack$ $\lbrack 0;4\rbrack$.

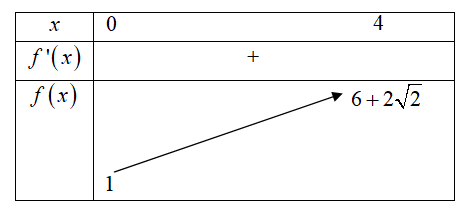
Để bất phương trình đã cho có nghiệm thì $m > 1$.

Do $m$ nguyên và thuộc khoảng $( - 10;10)$ nên $m \in \left\{ 2;3;...;9 \right\}$ $m \in \left\{ 2;3;...;9 \right\}$.

Vậy có 8 giá trị $m$ nguyên cần tìm là : $m \in \left\{ 2;3;...;9 \right\}$ $m \in \left\{ 2;3;...;9 \right\}$.

Ví dụ 3. Tìm tất cả các giá trị thực của tham số $m$ để bất phương trình $\log_{2}(5^{x} - 1).\log_{2}(2.5^{x} - 2) \geq m$ $\log_{2}(5^{x} - 1).\log_{2}(2.5^{x} - 2) \geq m$ có nghiệm $x \geq 1$ $x \geq 1$.

Hướng dẫn giải

Với $x \geq 1$ $x \geq 1$ thì $5^{x} - 1 > 0;\ \ 2.5^{x} - 2 > 0$ $5^{x} - 1 > 0;\ \ 2.5^{x} - 2 > 0$.

Ta có: $\log_{2}(5^{x} - 1).\log_{2}(2.5^{x}- 2) \geq m$ $\log_{2}(5^{x} - 1).\log_{2}(2.5^{x}- 2) \geq m$

$\Leftrightarrow \log_{2}(5^{x} -1).\log_{2}(2.5^{x} - 2) \geq m$ $\Leftrightarrow \log_{2}(5^{x} -1).\log_{2}(2.5^{x} - 2) \geq m$

$\Leftrightarrow \log_{2}(5^{x} -1).\left\lbrack 1 + \log_{2}(5^{x} - 1) \right\rbrack \geq m$ $\Leftrightarrow \log_{2}(5^{x} -1).\left\lbrack 1 + \log_{2}(5^{x} - 1) \right\rbrack \geq m$.

Đặt $t = \log_{2}\left( 5^{x} - 1\right)$ $t = \log_{2}\left( 5^{x} - 1\right)$ do $x \geq 1 \Rightarrow t \in \lbrack 2; + \infty)$ $x \geq 1 \Rightarrow t \in \lbrack 2; + \infty)$.

BPT trở thành: $t(1 + t) \geq m \Leftrightarrow t^{2} + t \geq m$ $t(1 + t) \geq m \Leftrightarrow t^{2} + t \geq m$.

Đặt $f(t) = t^{2} + t$ $f(t) = t^{2} + t$ ta có $f'(t) = 2t + 1 > 0$ với $\forall t \in (2; + \infty)$ $\forall t \in (2; + \infty)$ nên hàm số $y = f(t)$ đồng biến và liên tục trên $\lbrack 2; + \infty)$ $\lbrack 2; + \infty)$.

Suy ra $f(t) \in \lbrack 6; + \infty)$ $f(t) \in \lbrack 6; + \infty)$ khi $t \in \lbrack 2; + \infty)$ $t \in \lbrack 2; + \infty)$.

Do đó để để bất phương trình $\log_{2}(5^{x} - 1).\log_{2}(2.5^{x} - 2) \geq m$ $\log_{2}(5^{x} - 1).\log_{2}(2.5^{x} - 2) \geq m$ có nghiệm thỏa mãn $x \geq 1$ $x \geq 1$ thì $m\mathbb{\in R}$ $m\mathbb{\in R}$

C. Bài tập tự rèn luyện có đáp án chi tiết

Bài tập 1. Có bao nhiêu số nguyên dương $m$ trong đoạn $\lbrack - 2018\ ;\ 2018\rbrack$ $\lbrack - 2018\ ;\ 2018\rbrack$ sao cho bất phương trình $(10x)^{m + \frac{\log x}{10}} \geq 10^{\frac{11}{10}\log x}$ $(10x)^{m + \frac{\log x}{10}} \geq 10^{\frac{11}{10}\log x}$ đúng với mọi $x \in (1\ ;\ 100)$ $x \in (1\ ;\ 100)$?

Bài tập 2. Tìm tất cả các giá trị thực của tham số $m$để bất phương trình $\log_{\frac{1}{2}}(x - 1) >\log_{\frac{1}{2}}\left( x^{3} + x - m \right)$ $\log_{\frac{1}{2}}(x - 1) >\log_{\frac{1}{2}}\left( x^{3} + x - m \right)$ có nghiệm.

Bài tập 3. Có tất cả bao nhiêu giá trị nguyên của $m \in \lbrack - 2021;2022\rbrack$ $m \in \lbrack - 2021;2022\rbrack$ để bất phương trình $\log_{3}^{2}3x +\sqrt{\log_{3}^{2}x + 1} + 2\log_{\frac{1}{3}}x - 2m - 2 \leq 0$ $\log_{3}^{2}3x +\sqrt{\log_{3}^{2}x + 1} + 2\log_{\frac{1}{3}}x - 2m - 2 \leq 0$ có nghiệm với mọi $x$ thuộc đoạn $\left\lbrack 1\ ;\ \ 3^{\sqrt{3}} \right\rbrack$ $\left\lbrack 1\ ;\ \ 3^{\sqrt{3}} \right\rbrack$?

Bài tập 4. Cho hàm số $f(x) = \frac{x^{2} + x + 1}{x^{2} + 1}$ $f(x) = \frac{x^{2} + x + 1}{x^{2} + 1}$. Tìm tất cả các giá trị thực của tham số $m$ để bất phương trình $2^{f^{2}(x) - 4f(x)} + \log_{5}\left\lbrack f(x) +\frac{4}{f(x)} \right\rbrack \geq m$ $2^{f^{2}(x) - 4f(x)} + \log_{5}\left\lbrack f(x) +\frac{4}{f(x)} \right\rbrack \geq m$ có nghiệm $x \in (0; + \infty)$ $x \in (0; + \infty)$.

---------------------------------------------------

Qua bài viết này, bạn đã nắm được cách tìm m để bất phương trình logarit có nghiệm trên tập D, hiểu rõ phương pháp giải bất phương trình logarit chứa tham số và bản chất điều kiện xác định của logarit. Hãy luyện tập thêm các bài tập logarit nâng cao, đối chiếu đáp án và phân tích lời giải để củng cố kiến thức, từ đó tự tin chinh phục các dạng toán logarit trong mọi đề thi.

Tải về

Chọn file muốn tải về:

Tìm m để bất phương trình logarit có nghiệm trên tập D

539,4 KB

(File word) Tìm m để bất phương trình logarit có nghiệm trên tập D

Chia sẻ bởi:
Nhân Mã

1

3

Bài trước

Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!