Vật lí 11 Chân trời sáng tạo bài 3

Năng lượng trong dao động điều hòa

Vật lí 11 Chân trời sáng tạo bài 3: Năng lượng trong dao động điều hòa

Bài 1 trang 25 SGK Vật lí 11 Chân trời
Bài 2 trang 25 SGK Vật lí 11 Chân trời

Vật lí 11 Chân trời sáng tạo bài 3: Năng lượng trong dao động điều hòa được VnDoc.com tổng hợp lời giải bài tập Vật lý 11 Chân trời sáng tạo. Mời các bạn cùng theo dõi bài viết dưới đây nhé.

Bài 1 trang 25 SGK Vật lí 11 Chân trời

Một hệ dao động điều hoà với chu kì 2s. Chọn gốc thế năng tại vị trí cân bằng của vật. Thời điểm hệ bắt đầu dao động thì động năng và thế năng bằng nhau lần thứ nhất. Hỏi sau bao lâu kể từ khi hệ bắt đầu dao động, động năng và thế năng bằng nhau lần thứ hai?

Lời giải

Hệ dao động điều hoà với chu kì 2 s nên tần số góc là: $\omega=\pi (rad/s)$ $\omega=\pi (rad/s)$

Động năng và thế năng bằng nhau lần thứ nhất thì:

$W_{t}=W_{d} \Rightarrow \frac{1}{2}m\omega ^{2}A^{2}cos^{2}(\omega t+\varphi _{0})=\frac{1}{2}m\omega^{2}A^{2}sin^{2}(\omega t+\varphi _{0})$ $W_{t}=W_{d} \Rightarrow \frac{1}{2}m\omega ^{2}A^{2}cos^{2}(\omega t+\varphi _{0})=\frac{1}{2}m\omega^{2}A^{2}sin^{2}(\omega t+\varphi _{0})$

$\Rightarrow cos^{2}(\pi t+\varphi _{0})=sin^{2}(\pi t+\varphi _{0})$ $\Rightarrow cos^{2}(\pi t+\varphi _{0})=sin^{2}(\pi t+\varphi _{0})$

$\Rightarrow \pi t+\varphi _{0}=\frac{\pi}{4}+\frac{k\pi}{2}$ $\Rightarrow \pi t+\varphi _{0}=\frac{\pi}{4}+\frac{k\pi}{2}$

Lần thứ nhất động năng và thế năng bằng nhau nên k = 1, t = 0 nên ta có: $\varphi _{0}=\frac{3\pi}{4}$ $\varphi _{0}=\frac{3\pi}{4}$

Động năng và thế năng bằng nhau lần thứ hai sau khoảng thời gian:

$\pi t+\frac{3\pi}{4}=\frac{\pi}{4}+\frac{2\pi}{2}\Rightarrow t=0,5 s$ $\pi t+\frac{3\pi}{4}=\frac{\pi}{4}+\frac{2\pi}{2}\Rightarrow t=0,5 s$

Bài 2 trang 25 SGK Vật lí 11 Chân trời

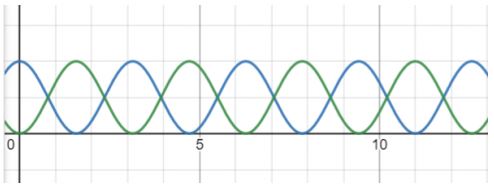
Xét một vật bắt đầu dao động điều hoà từ vị trí cân bằng theo chiều âm của trục toạ độ. Chọn gốc thế năng tại vị trí cân bằng của vật. Hãy vẽ phác đồ thị thể hiện sự phụ thuộc vào thời gian của động năng và thế năng trong hai chu kì dao động trên cùng một hệ trục toạ độ. Chỉ ra trên đồ thị những thời điểm mà động năng và thế năng có độ lớn bằng nhau.

Lời giải

Phương trình dao động của vật là: $x=Acos(\omega t-\frac{\pi}{2})$ $x=Acos(\omega t-\frac{\pi}{2})$

Thế năng của dao động là: $W_{t}=\frac{1}{2}m\omega ^{2}A^{2}cos^{2}(\omega t-\frac{\pi}{2})$ $W_{t}=\frac{1}{2}m\omega ^{2}A^{2}cos^{2}(\omega t-\frac{\pi}{2})$

Động năng của dao động là: $W_{d}=\frac{1}{2}m\omega^{2}A^{2}sin^{2}(\omega t-\frac{\pi}{2})$ $W_{d}=\frac{1}{2}m\omega^{2}A^{2}sin^{2}(\omega t-\frac{\pi}{2})$

Đường màu xanh lá cây là thế năng, đường màu xanh nước biển là động năng

Trên đồ thị những thời điểm mà hai đồ thị cắt nhau thì động năng và thế năng có độ lớn bằng nhau

$\frac{T}{8}+k\frac{T}{4}$ $\frac{T}{8}+k\frac{T}{4}$

Vật lí 11 Chân trời sáng tạo bài 3

---------------------------------------

Bài tiếp theo: Vật lí 11 Chân trời sáng tạo bài 4

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Vật lí 11 Chân trời sáng tạo bài 3: Năng lượng trong dao động điều hòa. Mong rằng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Vật lí 11 Chân trời sáng tạo. Mời các bạn cùng tham khảo thêm tại mục Hóa học 11 Chân trời sáng tạo, Toán 11 Chân trời sáng tạo.

Chia sẻ, đánh giá bài viết

1

127

Bài trước

Bài sau