Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Thể tích khối lăng trụ

Bài tập thể tích toán 11

Bài trước

Tải về

Bài sau

Lớp: Lớp 11

Môn: Toán

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Bài tập thể tích khối lăng trụ có lời giải

Hình lăng trụ
Công thức tính Thể tích khối lăng trụ
Ví dụ minh họa tính thể tích khối lăng trụ
Bài tập vận tính thể tích khối lăng trụ

Trong chương trình Toán 11, dạng toán thể tích khối lăng trụ là nội dung quan trọng của hình học không gian, thường xuất hiện trong các bài kiểm tra và đề thi. Việc nắm vững công thức và phương pháp tính thể tích lăng trụ giúp học sinh giải toán nhanh và chính xác hơn.

Hình lăng trụ

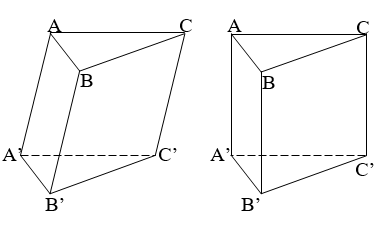
Công thức tính Thể tích khối lăng trụ

$\boxed{V = B.h}$

Diện tích mặt đáy.

Chiều cao của khối chóp

Lưu ý: Lăng trụ đứng có chiều cao cũng là cạnh bên.

Ví dụ minh họa tính thể tích khối lăng trụ

Ví dụ 1. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng là:

A. $\frac{a^{3}\sqrt{3}}{4} \cdot$ B. $\frac{a^{3}\sqrt{3}}{3} \cdot$ C. $\frac{a^{3}\sqrt{2}}{3} \cdot$ D. $\frac{a^{3}\sqrt{2}}{2} \cdot$

Hướng dẫn giải

Hình vẽ minh họa:

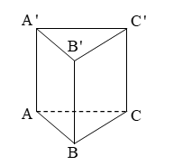
Ta có: $\left\{ \begin{matrix} h = a \\ S = \frac{a^{2}\sqrt{3}}{4} \end{matrix} \right.\ \ \ \ \Rightarrow V = h.S = \frac{a^{3}\sqrt{3}}{4}$

Ví dụ. Cho lăng trụ ABCD.A'B'C'D' có là hình chữ nhật, A'A = A'B = A'D . Tính thể tích khối lăng trụ biết , $AD = a\sqrt{3}$ , AA' =
2a .

A. $3a^{3}$ . B. $a^{3}$ . C. $a^{3}\sqrt{3}$ . D. $3a^{3}\sqrt{3}$ .

Hướng dẫn giải

Hình vẽ minh họa:

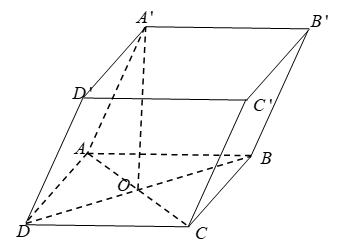
Gọi là giao điểm của và .

là hình chữ nhật $\Rightarrow OA = OB = OD$

Mà A'A = A'B = A'D nên $A'O\bot(ABD)$ (vì A'O là trực tâm giác )

$\Delta ABD$ vuông tại $\Rightarrow BD = \sqrt{AB^{2} + AD^{2}} = 2a$

$\Rightarrow OA = OB = OD = a$

$\Delta AA'O$ vuông tại $\Rightarrow A'O = \sqrt{AA'^{2} - AO^{2}} = a\sqrt{3}$

$S_{ABCD} = AB.AD = a^{2}\sqrt{3}$

$V_{ABCDA'B'C'D'} = A'O.S_{ABCD} = 3a^{3}$ .

Ví dụ. Cho lăng trụ ABC.A'B'C' có là tam giác vuông tại . Hình chiếu của lên là trung điểm của . Tính thể tích khối lăng trụ biết , $AC = a\sqrt{3}$ , AA' =
2a .

A. $\frac{a^{3}}{2} \cdot$ B. $\frac{3a^{3}}{2} \cdot$ C. $a^{3}\sqrt{3}$ . D. $3a^{3}\sqrt{3}$ .

Hướng dẫn giải

Hình vẽ minh họa:

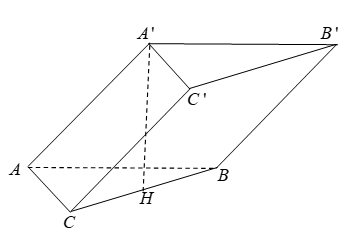
Gọi là trung điểm của $\Rightarrow A'H\bot(ABC)$ .

là tam giác vuông tại

$\Rightarrow BC = \sqrt{AB^{2} + AC^{2}} = 2a$

$\Rightarrow AH = \frac{1}{2}BC = a$

$\Delta A'AH$ vuông tại $\Rightarrow A'H = \sqrt{AA'^{2} - AH^{2}} = a\sqrt{3}$

$S_{\Delta ABC} = \frac{1}{2}AB.AC = \frac{a^{2}\sqrt{3}}{2}$

$V_{ABCA'B'C'} = A'H.S_{ABC} = \frac{3a^{3}}{2}$

Bài tập vận tính thể tích khối lăng trụ

Bài tập 1. Cho lăng trụ ABCD.A'B'C'D' có là hình thoi. Hình chiếu của lên là trọng tâm của tam giác . Tính thể tích khối lăng trụ ABCA'B'C' biết , $\widehat{ABC} = 120^{0}$ , AA' = a .

A. $a^{3}\sqrt{2}$ . B. $\frac{a^{3}\sqrt{2}}{6} \cdot$ C. $\frac{a^{3}\sqrt{2}}{3} \cdot$ D. $\frac{a^{3}\sqrt{2}}{2} \cdot$

Bài tập 2. Cho lăng trụ ABC.A'B'C' . Tính tỉ số $\frac{V_{ABB'C'}}{V_{ABCA'B'C'}}$ .

A. $\frac{1}{2} \cdot$ B. $\frac{1}{6} \cdot$ C. $\frac{1}{3} \cdot$ D. $\frac{2}{3}$ .

Bài tập 3. Lăng trụ tam giác ABC.A'B'C' có đáy tam giác đều cạnh , góc giữa cạnh bên và mặt đáy bằng 30⁰. Hình chiếu lên là trung điểm của . Thể tích khối lăng trụ là

A. $\frac{a^{3}\sqrt{3}}{6} \cdot$ B. $\frac{a^{3}\sqrt{3}}{2} \cdot$ C. $\frac{a^{3}\sqrt{3}}{12} \cdot$ D. $\frac{a^{3}\sqrt{3}}{8} \cdot$

Bài tập 4. Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông tại , , mặt phẳng (A'BC) tạo với đáy một góc $30{^\circ}$ và tam giác A'BC có diện tích bằng $a^{2}\sqrt{3}$ . Tính thể tích khối lăng trụ .

A. $\frac{a^{3}\sqrt{3}}{8}$ . B. $\frac{3a^{3}\sqrt{3}}{4}$ . C. $\frac{3a^{3}\sqrt{3}}{8}$ . D. $\frac{3a^{3}\sqrt{3}}{2}$ .

📥 Để xem trọn vẹn nội dung và ví dụ minh họa, bạn vui lòng tải tài liệu tham khảo tại đây.

-------------------------------------------------------

Chuyên đề thể tích khối lăng trụ giúp học sinh hiểu rõ công thức và cách áp dụng trong Toán 11. Luyện tập thường xuyên dạng toán này sẽ giúp bạn nâng cao kỹ năng giải toán hình học không gian và đạt kết quả tốt trong học tập.

Xem thử Tải về

Chọn file muốn tải về: