Trong mặt phẳng Oxy cho đường thẳng . Phép tịnh tiến theo vectơ
biến d thành đường thẳng d' có phương trình?
Vì
|
Sai lầm |
Nguyên nhân |
|
Giải sai |
|
|
Giải sai |
|
|
Giải sai |
Vậy đáp án cần tìm là: .
Trong chương trình Toán 11, phép dời hình là nội dung quan trọng giúp học sinh hiểu rõ bản chất các phép biến hình như tịnh tiến, đối xứng và phép quay. Bài viết Trắc nghiệm Phép dời hình Toán 11 Có đáp án cung cấp hệ thống câu hỏi trắc nghiệm online được chọn lọc theo mức độ từ cơ bản đến nâng cao. Thông qua việc luyện tập trực tiếp và kiểm tra đáp án ngay sau mỗi câu, bạn sẽ củng cố kiến thức, rèn kỹ năng làm bài nhanh và chuẩn xác hơn.
Trong mặt phẳng Oxy cho đường thẳng . Phép tịnh tiến theo vectơ
biến d thành đường thẳng d' có phương trình?
Vì
|
Sai lầm |
Nguyên nhân |
|
Giải sai |
|
|
Giải sai |
|
|
Giải sai |
Vậy đáp án cần tìm là: .
Phép quay biến điểm
thành
. Khi đó
(I) cách đều
và
.
(II) thuộc đường tròn đường kính
.
(III) nằm trên cung chứa góc
dựng trên đoạn
.
Trong các câu trên câu đúng là
Ta có: suy ra
+ nên (I) đúng.
+ (II) xảy ra khi vuông tại
, nói chung điều này không đúng, nên (II) sai.
+ nên (III) sai.
Cho đa giác đều có tâm
như hình bên.
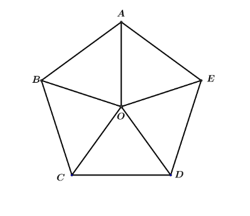
Hãy cho biết phép biến hình nào biến tam giác thành tam giác
?
Quay ngược chiều dương vòng tròn lượng giác nên góc quay là .
Trong mặt phẳng Oxy cho
và đường thẳng
. Ảnh của đường thẳng d qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay
và phép tịnh tiến theo vectơ
là đường thẳng d’ có phương trình:
Qua phép tịnh tiến
Qua phép quay
Nhận xét: Vì từ đó loại được đáp án
.
Do đó chỉ cần tìm được đến phương trình là có thể chọn ngay đáp án
.
Cho hình vuông có tâm
, gọi
lần lượt là trung điểm của các cạnh
. Qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm
, góc
và phép tịnh tiến theo véc tơ
. Thì ảnh của hình vuông
là:
Hình vuông (Đúng vì
)
Hình vuông (Chỉ thực hiện phép quay)
Hình vuông (Chỉ thực hiện phép tịnh tiến theo véc tơ
)
Hình vuông (Sai thứ tự các đỉnh)
Trong mặt phẳng Oxy cho điểm . Phép quay tâm O góc quay
biến A thành điểm có tọa độ nào trong các tọa độ sau?
Ta có:
|
Sai lầm |
Nguyên nhân |
|
Sai công thức: |
|
|
Sai công thức: |
|
|
Sai công thức: |
Vậy ảnh của điểm A cần tìm là:
Cho phép dời hình F có quy tắc đặt ảnh tương ứng điểm có ảnh là điểm
theo công thức
. Viết phương trình elip
là ảnh của elip
qua phép dời hình F.
Với , theo quy tắc:
thay vào
ta có:
Cho phép dời hình F có quy tắc đặt ảnh tương ứng điểm có ảnh là điểm
theo công thức
. Viết phương trình đường thẳng
là ảnh của đường thẳng
qua phép dời hình F.
Với , theo quy tắc:
thay vào
ta có:
Trên chiếc đồng hồ treo tường từ lúc 4 giờ đến 4 giờ 40 phút, kim phút đã quay được một góc bao nhiêu độ?
(Sai do hiểu nhầm 40 phút là
)
(Đúng theo đ/n phép quay)
(Sai do hiểu nhầm hướng quay)
(Sai do hiểu nhầm kim đồng hồ quay theo chiều dương)
Cho phép dời hình F có quy tắc đặt ảnh tương ứng điểm có ảnh là điểm
theo công thức
. Tìm tọa độ điểm P có ảnh là điểm
qua phép dời hình F.
Ta có
Trong mặt phẳng Oxy cho đường tròn . Phép tịnh tiến theo vectơ
biến
thành đường tròn
có phương trình?
Vì
|
Sai lầm |
Nguyên nhân |
|
Sai |
|
|
Sai công thức |
|
Vậy ảnh của đường tròn cần tìm là .
Trong các mệnh đề sau, mệnh đề nào đúng?
Thực hiện liên tiếp hai phép tịnh tiến sẽ được một phép tịnh tiến trong đó vectơ tịnh tiến bằng tổng của 2 vectơ tịnh tiến của hai phép đã cho.
Trong mặt phẳng Oxy cho đường thẳng . Phép quay tâm O góc quay
biến d thành đường thẳng d' có phương trình?
Vì
|
Sai lầm |
Nguyên nhân |
|
Giải sai |
|
|
Giải sai |
|
|
Giải sai |
Vậy đáp án cần tìm là:
Trong mặt phẳng Oxy cho điểm . Phép dời hình bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ
và phép quay tâm O góc quay 900 biến A thành điểm có tọa độ nào trong các tọa độ sau?
Qua phép tịnh tiến
Qua phép quay
|
Sai lầm |
Nguyên nhân |
|
Qua phép tịnh tiến Qua phép quay |
|
|
Qua phép tịnh tiến Qua phép quay |
|
|
Qua phép tịnh tiến Qua phép quay |
Đáp án cần tìm là: .
Cho phép dời hình F có quy tắc đặt ảnh tương ứng điểm có ảnh là điểm
theo công thức
. Tính độ dài đoạn thẳng PQ với P, Q tương ứng là ảnh của hai điểm
qua phép dời hình F.
Theo quy tắc, ta có:
.
Cho phép dời hình F có quy tắc đặt ảnh tương ứng điểm có ảnh là điểm
theo công thức
. Viết phương trình đường tròn
là ảnh của đường tròn
qua phép dời hình F.
Theo công thức thay vào
ta có:
Trong mặt phẳng với hệ trục tọa độ, cho phép tịnh tiến theo
, phép tịnh tiến theo
biến parabol
thành parabol
. Khi đó phương trình của
là:
Chọn tùy ý trên
. Gọi
.
Vì nên
.
Ta có
.
Suy ra
Vì nên
.
Suy ra .
Vậy: .
Cho phép dời hình F có quy tắc đặt ảnh tương ứng điểm có ảnh là điểm
theo công thức
. Viết phương trình đường tròn
là ảnh của đường tròn
qua phép dời hình F.
Gọi (1)
Với , theo quy tắc:
thay vào (1) ta có:
.
Trong mặt phẳng Oxy cho ba điểm và
. Phép tịnh tiến theo vectơ
biến điểm M thành điểm có tọa độ nào trong các tọa độ sau?
Vì
|
Sai lầm |
Nguyên nhân |
Vậy đáp án cần tìm là:
Cho phép dời hình F có quy tắc đặt ảnh tương ứng điểm có ảnh là điểm
theo công thức
. Tìm tọa độ điểm A có ảnh là điểm
qua phép dời hình F.
Ta có
Cho hình vuông ABCD tâm O. Gọi M, N lần lượt là trung điểm của AB và AD (hình bên).
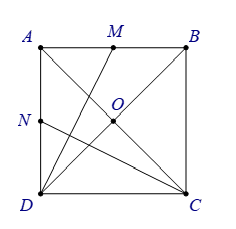
Theo hình bên thì khẳng định nào sau đây là khẳng định SAI:
Xét đáp án “Góc giữa DM và CN bằng ”
Dễ dàng chứng minh mà
. Từ đó ta có Góc giữa DM và CN bằng
.
Xét đáp án “Tam giác ODC là ảnh của tam giác OAB qua phép quay tâm O góc quay ” Đúng theo tính chất phép quay
Xét đáp án “Đường thẳng DM là ảnh của đường thẳng CN qua phép quay tâm O góc quay “ Đúng theo tính chất phép quay
Xét đáp án “Tam giác OBC là ảnh của tam giác qua phép quay tâm O góc quay
» Sai vì góc quay là
.
Cho hình vuông ABCD ( như hình vẽ).
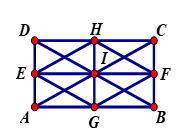
Phép dời hình nào sau đây biến tam giác DEI thành tam giác CFI?
Phép dời hình biến tam giác DEI thành tam giác CFI là phép quay tâm H góc 900.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
