Ảnh của đường thẳng qua phép quay tâm
góc quay
là đường thẳng
có phương trình
Có . Lấy
.
Gọi thì
.
Do nên
.
Bạn đã nắm vững kiến thức cơ bản về phép quay và muốn nâng cao khả năng vận dụng? Bộ Trắc nghiệm Toán 11 Phép quay (mức độ thông hiểu) dưới đây sẽ giúp bạn rèn luyện tư duy, hiểu sâu bản chất phép biến hình và giải thích được cách hình ảnh thay đổi sau phép quay. Với hình thức bài tập Toán 11 online có đáp án, học sinh có thể tự kiểm tra, đối chiếu lời giải và cải thiện kỹ năng một cách hiệu quả.
Ảnh của đường thẳng qua phép quay tâm
góc quay
là đường thẳng
có phương trình
Có . Lấy
.
Gọi thì
.
Do nên
.
Trong mặt phẳng Oxy, ảnh của điểm qua phép quay
là:
Gọi
Ta có:
Khi đó tọa độ điểm M’(x’; y’) được xác định như sau:
Suy ra:
Trong mặt phẳng , điểm
có ảnh là điểm nào qua phép quay tâm
góc quay
?
Gọi là ảnh của điểm
qua phép quay tâm
góc quay
.
Khi đó ta có .
Áp dụng công thức trên ta có.
Điểm có ảnh là điểm
qua phép quay tâm
góc quay
.
Phép quay với
biến điểm
thành
. Khi đó:
(I): cách đều
và
.
(II): thuộc đường tròn đường kính
.
(III): nằm trên cung chứa góc
dựng trên đoạn
.
Trong các câu trên câu đúng là:
(I) đúng theo định nghĩa có .
(II) chỉ đúng khi .
(III) chỉ đúng khi .
Cho tam giác đều , với góc quay nào sau đây thì phép quay tâm
có thể biến điểm
thành điểm
?
Đáp án cần tìm .
Cho tam giác đều . Hãy xác định góc quay của phép quay tâm
biến
thành
Hình vẽ minh họa:
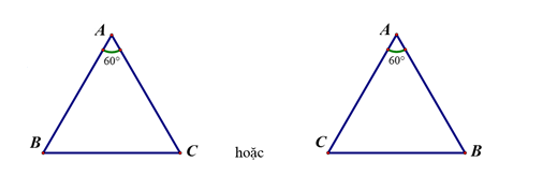
Ta có nên để phép quay tâm
với góc quay
biến
thành
thì
hoặc
.
Trong mặt phẳng cho hình vuông có tâm
, góc
. Khi đó ảnh của điểm
qua phép quay tâm
góc quay
là điểm nào?
Hình vẽ minh họa:

Vì nên thứ tự các điểm
cùng chiều kim đồng hồ.
Do đó .
Cho hình chữ nhật có là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm
góc
,
, biến hình chữ nhật trên thành chính nó?
Với điều kiện thì có
giá trị tìm được của
là
,
và
.
Trong mặt phẳng Oxy, qua phép quay ,
là ảnh của điểm:
Gọi
Ta có:
Khi đó tọa độ điểm M’(x’; y’) được xác định như sau:
Suy ra: thay vào (*) ta được:
Trong mặt phẳng cho đường thẳng
. Viết phương trình đường thẳng
với
là ảnh của
qua phép quay tâm
góc quay
.
Ta có vuông góc với
nên
có dạng
.
Lấy , ảnh
của
qua phép quay tâm
góc quay
là
.
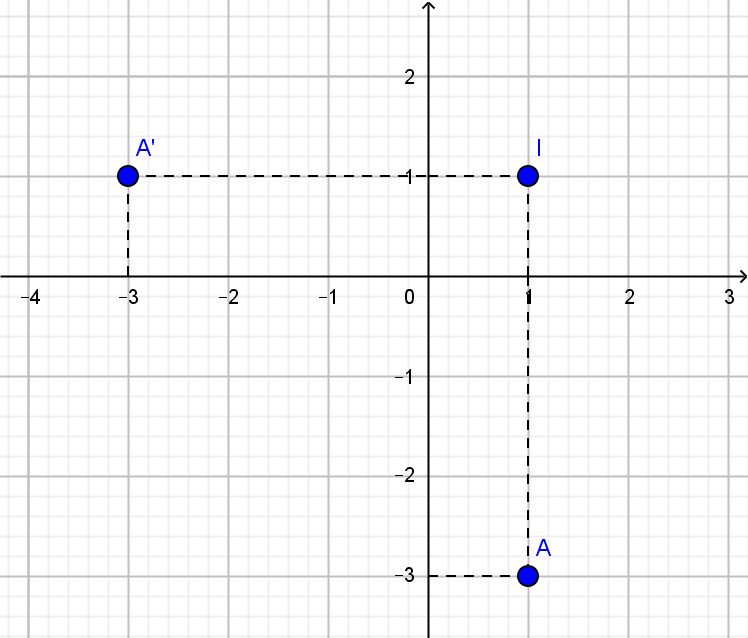
Nên có phương trình
.
Trong mặt phẳng , cho đường thẳng
. Viết phương trình của đường thẳng
là ảnh của đường thẳng
qua phép quay tâm
góc
.
Lấy . Gọi
thì
và
Vậy .
Trong mặt phẳng tọa độ cho phép quay tâm
biến điểm
thành điểm
. Khi đó nó biến điểm
thành điểm:
Ta có: ,
. Do
nên góc quay
.
Ta thấy nên góc suy ra góc quay
.
Gọi ảnh của qua phép quay tâm
, góc quay
là
.
Ta có: . Vậy:
.
Cho tam giác đều tâm . Hỏi có bao nhiêu phép quay tâm
góc
,
, biến tam giác trên thành chính nó?
Với điều kiện thì có
giá trị tìm được của
là
,
,
và
.
Trong mặt phẳng tọa độ cho đường thẳng có
, ảnh
của
qua phép quay tâm O, góc quay
là:
Gọi sao cho
Do đó chọn .
Trong mặt phẳng , cho điểm
. Hỏi các điểm sau điểm nào là ảnh của
qua phép quay tâm
, góc
?
Dựa vào hình vẽ chọn đáp án .
Chú ý: trong 4 đáp án chỉ có 1 đáp án điểm nằm trên trục nên chọn đáp án
.
Có bao nhiêu điểm biến thành chính nó qua phép quay tâm góc
,
là số nguyên?
Với góc ,
là số nguyên thì có duy nhất một điểm là
.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
