Đại cương về dao động điều hòa

GIÁO TRÌNH VẬT LÝ 12 LUYỆN THI THPT, ĐẠI HỌC, CAO ĐẲNG

Đại cương về dao động điều hòa được VnDoc.com sưu tầm và đăng tải, do tác giả Tri Nguyễn biên soạn. Đây là tài liệu bao gồm cả lý thuyết và bài tập về dạng bài dao động điều hòa trong Vật lý, giúp các bạn củng cố và luyện tập tốt, chuẩn bị cho kì thi THPT Quốc gia sắp tới.

• Đề cương ôn thi THPT Quốc gia năm 2020 môn Hóa học
• Đề cương ôn thi THPT Quốc gia năm 2020 môn Toán
• Tài liệu ôn thi THPT Quốc gia năm 2020 môn Vật lý

CHƯƠNG I: DAO ĐỘNG CƠ HỌC

CHỦ ĐỀ 1: ĐẠI CƯƠNG VỀ DAO ĐỘNG ĐIỀU HÒA

A. TÓM TẮT KIẾN THỨC CƠ BẢN

I. DAO ĐỘNG TUẦN HOÀN

1. Định nghĩa: là dao động mà trạng thái chuyển động của vật được lặp lại như cũ sau những khoảng thời gian bằng nhau xác định.

2. Dao động tự do (dao động riêng)

+ Là dao động của hệ xảy ra dưới tác dụng chỉ của nội lực.

+ Là dao động có tần số (tần số góc, chu kỳ) chỉ phụ thuộc các đặc tính của hệ không phụ thuộc các yếu tố bên ngoài. Khi đó: ω gọi là tần số góc riêng; f gọi là tần số riêng; T gọi là chu kỳ riêng.

3. Chu kì, tần số của dao động:

+ Chu kì T của dao động điều hòa là khoảng thời gian để thực hiện một dao động toàn phần; đơn vị giây (s).

Với N là số dao động toàn phần vật thực hiện được trong thời gian t.

+ Tần số f của dao động điều hòa là số dao động toàn phần thực hiện được trong một giây; đơn vị héc (Hz).

II. DAO ĐỘNG ĐIỀU HÒA

1. Định nghĩa: là dao động mà trạng thái dao động được mô tả bởi định luật dạng cosin (hay sin) đối với thời gian.

2. Phương trình dao động: x = Acos(ωt + φ).

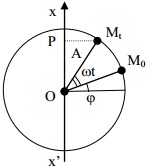
Các đại lượng đặc trưng của dao động điều hòa:

+ Li độ x: là độ lệch của vật khỏi vị trí cân bằng.

+ Biên độ A: là giá trị cực đại của li độ, luôn dương.

+ Pha ban đầu φ: xác định li độ x tại thời điểm ban đầu t = 0.

+ Pha của dao động (ωt + φ): xác định li độ x của dao động tại thời điểm t.

+ Tần số góc ω: là tốc độ biến đổi góc pha. Đơn vị: rad/s.

+ Biên độ và pha ban đầu có những giá trị khác nhau, tùy thuộc vào cách kích thích dao động.

+ Tần số góc có giá trị xác định (không đổi) đối với hệ vật đã cho.

3. Phương trình vận tốc:

+ Véctơ v luôn cùng chiều với chiều chuyển động (vật chuyển động theo chiều dương thì v > 0, theo chiều âm thì v < 0).

+ Vận tốc của vật dao động điều hòa biến thiên điều hòa cùng tần số nhưng sớm pha hơn π/2 so với với li độ.

+ Vị trí biên (x = ± A), v = 0. Vị trí cân bằng (x = 0), |v| = v_max = ωA.

4. Phương trình gia tốc: a = - ω²Acos(ωt + φ) = ω²Acos(ωt + φ + π) = - ω²x.

+ Véctơ a luôn hướng về vị trí cân bằng.

+ Gia tốc của vật dao động điều hòa biến thiên điều hòa cùng tần số nhưng ngược pha với li độ (sớm pha π/2 so với vận tốc).

+ Véctơ gia tốc của vật dao động điều hòa luôn hướng về vị trí cân bằng, có độ lớn tỉ lệ với độ lớn của li độ.

5. Hệ thức độc lập:

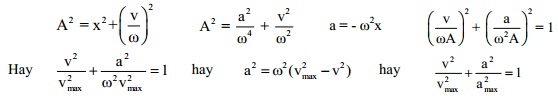
6. Vật ở VTCB: x = 0; IvI_Max = ω A; IaI_Min = 0.

Vật ở biên: x = ± A; IvI_Min = 0; IaI_Max = ω²A

7. Sự đổi chiều và đổi dấu của các đại lượng:

+ x, a và F đổi chiều khi qua VTCB, v đổi chiều ở biên.

+ x, a, v và F biến đổi cùng T, f và ω.

8. Bốn vùng đặc biệt cần nhớ

a. Vùng 1: x > 0; v < 0; a < 0

Chuyển động nhanh dần theo chiều (-) vì a.v > 0 và thế năng giảm, động năng tăng.

b. Vùng 2: x < 0; v < 0; a > 0

Chuyển động nhanh dần theo chiều (-) vì a.v < 0 và thế năng tăng, động năng giảm.

c. Vùng 3: x < 0; v > 0; a > 0

Chuyển động nhanh dần theo chiều (+) vì a.v > 0 và thế năng giảm, động năng tăng.
d. Vùng 4: x > 0; v > 0; a < 0

Chuyển động nhanh dần theo chiều (+) vì a.v < 0 và thế năng tăng, động năng giảm.

9. Mối liên hệ về pha của li độ (x), vận tốc (v) và gia tốc (a).

Theo hình 1.2 ta nhận thấy mối liên hệ về pha của li độ (x), vận tốc (v) và gia tốc (a):

φ_v = φ_x + và φ_a = φ_v + = φ_x +

10. Chiều dài quỹ đạo: 2A

11. Quãng đường đi trong 1 chu kỳ luôn là 4A; trong một nữa chu kỳ luôn là 2A.

Quãng đường đi trong T/4 chu kỳ là A khi vật đi từ VTCB đến vị trí biên hoặc ngược lại.

Thời gian vật đi được những quãng đường đặc biệt:

12. Thời gian, quãng đƣờng, tốc độ trung bình

a. Thời gian: Giải phương trình

x_i = Acos(ωt_i+φ) tìm t_i

Chú ý:

Gọi O là trung điểm của quỹ đạo CD và M là trung điểm của OD; thời gian đi từ O đến M là t_OM = T/12 thời gian đi từ M đến D là t_MD = T/6

Từ vị trí cân bằng x = 0 ra vị trí x = ± A mất khoảng thời gian t = T/8

Từ vị trí cân bằng x = 0 ra vị trí x = ± A mất khoảng thời gian t = T/6

Chuyển động từ O đến D là chuyển động chậm dần đều, chuyển động từ D đến O là chuyển động nhanh dần đều

Trên đây VnDoc.com vừa giới thiệu tới các bạn Đại cương về dao động điều hòa. Mong rằng qua đây các bạn có thể học tập tốt hơn môn Vật lý lớp 12 nhé. Mời các bạn cùng tham khảo thêm các môn Toán 12, Ngữ văn 12, Tiếng Anh 12, đề thi học kì 1 lớp 12, đề thi học kì 2 lớp 12...