VnDoc.com

Đề thi học sinh giỏi môn Toán lớp 6 năm học 2019 - 2020

Đề thi HSG lớp 6 môn Toán có đáp án

VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí

�ᷫ苸͙ ͙IÁO DỤC VÀ ĐÀO TẠO

ĐỀ C�Í苸� T�ỨC

(Đề thi gồm có 01 trang)

KỲ T�I C�Ọ苸 �ỌC SI苸� ͙IỎI T�CS CẤ �UYỆ苸

苸ĂM �ỌC 2019 - 2020

MÔ苸 T�I: TOÁ苸 – LỚ 6

Thời gian làm bài 120 phút, không kể thời gian giao đề

Câu 1. (4,0 điểm)

a) Thực hiện phép tính

   

540: 23,7 19,7 42 132 75 36 7317A      

 

 

10 10

8

2 .13 2 .65

2 .104

B





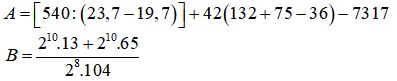
b) Chứng minh rằng tổng của 5 số tự nhiên chẵn liên tiếp thì chia hết cho 10,

còn tổng của 5 số tự nhiên lẻ liên tiếp chia cho 10 dư 5.

Câu 2. (4,0 điểm)

a) Tổng của hai số nguyên tố có thể bằng 2015 hay không? Vì sao?

b) Tìm tất cả các số nguyên tố p sao cho p + 11 cũng là số nguyên tố.

Câu 3. (4,0 điểm)

a) Tìm x biết:

       

1 3 5 99 0x x x x        

b) Tìm

n

biết

   

3 8 1n n 

.

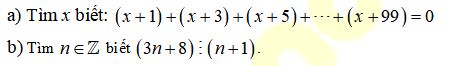
Câu 4. (4,0 điểm)

a) Tìm tích

1 1 1 1

2 3 4 100

     

   

     

     



b) So sánh A và B biết

2013.2014 1 2014.2015 1

2013.2014 2014.2015

A và B

 

 

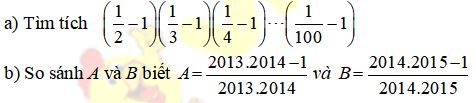
Câu 5. (4,0 điểm)

Cho đoạn thẳng AB; điểm O thuộc tia đối của tia AB. Gọi M, N thứ tự là trung

điểm của OA,OB.

a) Chứng tỏ rằng

OA OB

.

b) Trong ba điểm O, M, N điểm nào nằm giữa hai điểm còn lại?

c) Chứng tỏ rằng độ dài đoạn thẳng MN không phụ thuộc vào vị trí của điểm O

(O thuộc tia đối của tia AB).

----------------------- �ẾT ------------------------

Thí sinh không được sử dụng tài liệu; Cán bộ coi thi không giải thích gì thêm.

VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí

�ƯỚ苸͙ DẪ苸 C�ẤM TOÁ苸 6

(Hướng dẫn chấm gồm 02 trang)

Câu

苸ội dung

Điểm

Câu1

(4,0

điểm)

a) A = (540: 4) + 42.171 – 7317

A = 135 + 7182 – 7317 = 0

10 10

8

2 .13 2 .65

2 .104

B





=

10

8

2 13(1 5)

2 8 13

 

 

10

8 3

2 13 6

3

2 2 13

B

 

 

 

0,5

b) Gọi 5 số chẵn liên tiếp là:

2 ;2 2;2 4;2 6;2 8n n n n n   

Tính tổng ta được:

10 20 10n  

Gọi 5 số lẻ liên tiếp là:

2 1;2 3;2 5;2 7;2 n 9n n n n    

Tính tổng ta được:

 

10 25 10 2 5n n   

chia cho

10

dư

5

0,5

Câu 2

(4,0

điểm)

a) Tổng của hai số nguyên tố bằng 2015 là số lẻ, nên một trong hai

số nguyên tố phải là 2.

Khi đó số kia là 2013, số này là hợp số.

Vậy không tồn tại hai số nguyên tố có tổng bằng 2015.

1

0,5

b) Nếu p lẻ  p + 11 là số chẵn lớn hơn 11 nên không là số nguyên tố.

Suy ra p chẵn  p = 2.

1

Câu 3

(4,0

điểm)

a) Ta có :

       

1 3 5 99 0x x x x        

   

 

1 99 .50

0

2

50 .50 0

50 0

50

x x

x

  

 

 



 

 

0,5

b) Ta có 3n + 8 = 3n + 3 + 5 = 3 (n + 1) + 5

Suy ra

   

3 8 1n n 

khi (n + 1)



Ư(5)

Tức là

 

( 1) 1; 5n  

Tìm được

 

6; 2;0; 4n  

0,5

Câu 4

(4,0

điểm)

a) Ta có

1 1 1 1

2 3 4 100

     

    

     

     



1 2 1 3 1 4 1 100

2 2 3 3 4 4 100 100

     

    

     

     



1 2 3 99

2 3 4 100

   

   

 

1.2.3.4...99

2.3.4...100





0,5

VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí

1

100





b) Ta có

2013 2014 1 1

1

2013 2014 2013 2014

A

 

  

 

2014 2015 1 1

1

2014 2015 2014 2015

B

 

  

 

V

1 1

2013 2014 2014 2015



 

nên A < B

0,5

Câu 5

(4,0

điểm)

0,5

a) Hai tia OA và OB đối nhau nên điểm A nằm giữa hai điểm O và

B, suy ra OA < OB

0,5

b) Ta có M và N thứ tự là trung điểm của OA, OB nên

2

OA

OM 

;

2

OB

ON 

Vì

OA OB

nên

OM ON

Hai điểm M và N thuộc tia OB mà OM < ON nên điểm M nằm giữa

hai điểm O và N

0,5

c) Ta có

OM MN ON 

suy ra

MN ON OM 

hay

2 2

OB OA AB

MN



 

Vì

AB

có độ dài không đổi nên

MN

có độ dài không đổi.

0,5

(Nếu HS giải cách khác đúng vẫn cho điểm tối đa)

--------------------------HẾT------------------------

Tham khảo các đề thi HSG lớp 6:

https://vndoc.com/thi-hoc-sinh-gioi-lop-6

Đề thi học sinh giỏi môn Toán lớp 6

Đề thi học sinh giỏi môn Toán lớp 6 năm học 2019 - 2020 có đáp án chi tiết tham khảo dành cho các bạn học sinh và thầy cô nghiên cứu, học tập tốt môn Toán lớp 6 cũng như luyện tập và làm quen với nhiều đề học sinh giỏi hơn nhằm chuẩn bị tốt nhất cho các kì thi học sinh giỏi bậc THCS sắp diễn ra. Mời các bạn tham khảo.

Đề thi học sinh giỏi môn Toán lớp 6 bao gồm 5 câu hỏi tự luận có đáp án chi tiết cho từng câu hỏi giúp các em học sinh nắm được các kiến thức môn Toán, chuẩn bị cho các kì thi học sinh giỏi trong năm học đạt hiệu quả cao.