Tam giác

Chuyên đề Toán học lớp 6: Tam giác không chỉ cung cấp những định nghĩa nền tảng về tam giác mà còn tổng hợp các dạng bài tập đa dạng, từ nhận biết hình dạng đến các bài toán tính toán và chứng minh logic. Thông qua các ví dụ minh họa trực quan và lời giải chi tiết, bộ chuyên đề giúp học sinh củng cố tư duy hình học, rèn luyện kỹ năng giải toán chính xác và tự tin hơn trước các kỳ kiểm tra. Đây chắc chắn là nguồn tư liệu quý giá, đồng hành cùng các em trên con đường chinh phục kiến thức toán học lớp 6 một cách hiệu quả và đầy cảm hứng. Mời quý thầy cô và các em cùng tham khảo.

A. Lý thuyết

1. Tam giác ABC là gì?

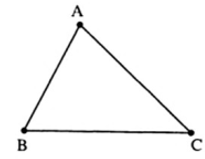
Định nghĩa: Tam giác ABC là hình gồm ba đoạn thẳng AB; BC; CA khi ba điểm A; B; C không thẳng hàng

Nhận xét: Một tam giác có: 3 cạnh, 3 đỉnh, 3 góc

Ví dụ: Tam giác ABC có ba cạnh AB; BC; CA ba đỉnh A; B; C và ba góc ∠A; ∠B; ∠C

Chú ý:

Một điểm nằm bên trong tam giác nếu nó nằm trong cả 3 góc của tam giác. Một điểm không nằm trong tam giác và không nằm trên cạnh nào của tam giác gọi là điểm ngoài của tam giác

B. Trắc nghiệm & Tự luận

I. Câu hỏi trắc nghiệm

Câu 1: Chọn câu đúng nhất: Tam giác ABC là hình có:

A. Ba cạnh AB; AC; BC B. Ba đỉnh A; B; C

C. Ba góc ∠A; ∠B; ∠C D. Cả A, B, C đều đúng

Tam giác ABC có ba cạnh AB; AC; BC, ba đỉnh A; B; C và ba góc ∠A; ∠B; ∠C.

Nên cả A, B, C đều đúng.

Chọn đáp án D.

Câu 2: Chọn câu sai khi nói về tam giác MNP

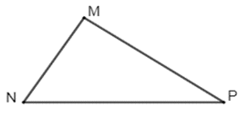
A. ΔMNP có 3 góc là: ∠MNP; ∠MPN; ∠PMN

B. ΔMNP có 3 đường thẳng là: MP; MN; PN

C. Ba điểm M; N; P không thẳng hàng

D. ΔMNP có 3 cạnh là: MN; PM; PN

Tam giác MNP có 3 góc là: ∠MNP; ∠MPN; ∠PMN; có 3 cạnh là: MN; PM; PN và ba điểm M; N; P không thẳng hàng nên A, C, D đúng.

Vì tam giác có ba cạnh là ba đoạn thẳng nên B sai.

Chọn đáp án B.

Câu 3: Cho 5 điểm A; B; C; D; E trong đó không có ba điểm nào thẳng hàng. Có bao nhiêu tam giác có các đỉnh là 3 trong 5 đỉnh trên:

A. 9 B. 10 C. 8 D. 7

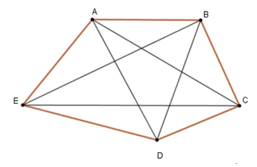
Có 10 tam giác mà các đỉnh là ba trong năm điểm đã cho là:

ΔABC; ΔABD; ΔABE; ΔBCD; ΔBCE; ΔCDA; ΔCDE; ΔDEB; ΔDEA; ΔAEC

Chọn đáp án B.

Câu 4: Cho đường thẳng d không đi qua O. Trên d lấy sáu điểm A; B; C; D; E; F phân biệt. Có bao nhiêu tam giác nhận điểm O làm đỉnh và hai đỉnh còn lại là hai trong 6 điểm A; B; C; D; E; F

A. 15 B. 12 C. 6 D. 9

Số tam giác tạo thành thỏa mãn điều kiện đề bài là: 6(6 - 1)/2 = 15 tam giác.

Chọn đáp án A.

Câu 5: Cho hình vẽ sau:

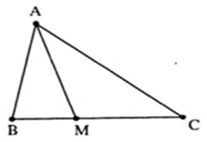
Kể tên các tam giác có trên hình vẽ:

A. ΔABM; ΔAMC; ΔABC B. ΔAMC; ΔABC C. ΔABM; ΔABC D. ΔABC

Các tam giác có trên hình vẽ là: ΔABM; ΔAMC; ΔABC

Chọn đáp án A.

Câu 6: Cho hình vẽ sau:

Kể tên các góc trong tam giác ABM:

Chọn đáp án A.

II. Bài tập tự luận

Câu 1: Vẽ hình liên tiếp theo các cách diễn đạt sau đây:

a) Vẽ tam giác ABC, có AB = 6cm, BC = 6cm và CA = 6cm

b) Vẽ tiếp các điểm M, N, P tương ứng là là trung điểm của AB, BC, CA

c) Vẽ tiếp tam giác MNP.

d) Đọc tên các đỉnh, các góc, các cạnh của tam giác có 3 đỉnh lấy từ các điểm A, B, C, M, N, P

Đáp án

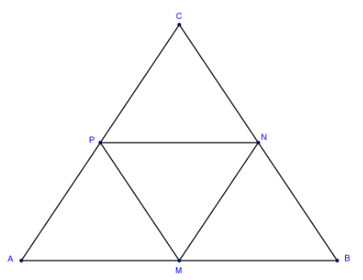
Các tam giác: ABC, AMP, MBN, MNP, PNC

Các đỉnh: A, B, C; A, M, P; M, B, N; M, N, P; P, N, C

Các góc: A, B, C; A, M, P; M, B, N; M, N, P; P, N, C

Các cạnh: AB, BC, CA; AM, MP, PA; MB, BN, MN; MN, MP, PM; PN, NC, CP

Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 6: Tam giác. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 6, Giải bài tập Toán lớp 6, Giải SBT Toán 6, Giải VBT Toán lớp 6 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc