Phân tích một số ra thừa số nguyên tố
Chuyên đề Toán học lớp 6: Phân tích một số ra thừa số nguyên tố được VnDoc sưu tầm, biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 6 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Phân tích một số ra thừa số nguyên tố
A. Lý thuyết
1. Phân tích một số ra thừa số nguyên tố là gì?
– Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
– Chú ý:
• Dạng phân tích ra thừa số nguyên tố của một số nguyên tố là chính số đó.
• Mọi hợp số đều phân tích được ra thừa số nguyên tố.
– Muốn phân tích một số ra thừa số nguyên tố ta dùng dấu hiệu chia hết cho các số nguyên tố 2, 3, 5,… Phép chia dừng lại khi có thương bằng 1.
2. Cách phân tích một số ra thừa số nguyên tố
• Phương pháp phân tích theo sơ đồ cây:

• Phương pháp phân tích theo sơ đồ cột:
Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.
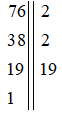
Như vậy 76 = 22.19
• Nhận xét: Dù phân tích một số ra thừa số nguyên tố bằng cách nào đi nữa thì cuối cùng cũng ra một kết quả.
B. Trắc nghiệm & Tự luận
I. Câu hỏi trắc nghiệm
Câu 1: Phân tích thừa số nguyên tố a = p1m1 . p2m2 . p3m3 ... pkmk, khẳng định nào sau đây đúng?
A. Các số p1; p2; ...; pk là các số dương.
B. Các số p1; p2; ...; pk là các số nguyên tố
C. Các số p1; p2; ...; pk là các số tự nhiên.
D. Các số p1; p2; ...; pk tùy ý.
Lời giải:
Khi phân tích một số a = p1m1 . p2m2 . p3m3 ... pkmk ra thừa số nguyên tố thì p1; p2; ...; pk là các số nguyên tố.
Chọn đáp án B.
Câu 2: Phân tích số 18 ra thừa số nguyên tố
A. 18 = 18 . 1
B. 18 = 10 + 8
C. 18 = 2 . 32
D. 18 = 6 + 6 + 6
Lời giải:
+ Đáp án A sai vì 1 không phải là số nguyên tố
+ Đáp án B sai vì đây là phép cộng.
+ Đáp án C đúng vì 2 và 3 là hai số nguyên tố nên 18 = 2 . 32
+ Đáp án D sai vì đây là phép cộng
Chọn đáp án C.
Câu 3: Cho a = 22 . 7, hãy viết tập hợp tất cả các ước của a
A. Ư(a) = {4; 7}
B. Ư(a) = {1; 4; 7}
C. Ư(a) = {1; 2; 4; 7; 28}
D. Ư(a) = {1; 2; 4; 7; 14; 28}
Lời giải:
Ta có: a = 22 . 7 = 4 . 7 = 28
28 = 28 . 1 = 14 . 2 = 7 . 4 = 7 . 2 . 2
Vậy Ư(28) = {1; 2; 4; 7; 14; 28}
Chọn đáp án D.
Câu 4: Cho a2 . b . 7 = 140, với a, b là các số nguyên tố, vậy a có giá trị bằng bao nhiêu?
A. 1
B. 2
C. 3
D. 4
Lời giải:
Ta có a2 . b . 7 = 140 ⇒ a2b = 20 = 22 . 5
Vậy giá trị của a là 2
Chọn đáp án B
Câu 5: Cho số 150 = 2 . 3 . 52, số lượng ước của 150 là bao nhiêu?
A. 6
B. 7
C. 8
D. 12
Lời giải:
Nếu m = axbycz, với a, b, c là số nguyên tố thì m có (x + 1)(y + 1)(z + 1) ước.
Ta có 150 = 2 . 3 . 52 với x = 1; y = 1; z = 2
Vậy số lượng ước số của 150 là (1 + 1)(1 + 1)(2 + 1) = 12 ước.
Chọn đáp án D.
II. Bài tập tự luận
Câu 1: Phân tích các số 120; 900; 100 000 ra thừa số nguyên tố
Ta có: 120 = 23 . 3 . 5
900 = 22 . 32 . 52
100 000 = 105 = 25.55
Câu 2: P hân tích số A = 26 406 ra thừa số nguyên tố. A có chia hết cho các số sau hay không như 21, 60, 91, 140, 150, 270?
Ta có: A = 26 406 = 22 . 33 . 5 . 72
Mặt khác ta cũng có:
21 = 3 . 7
60 = 22 . 3 . 5
91 = 7 . 13
140 = 22 . 5 . 7
150 = 2 . 3 . 52
270 = 2 . 33 . 5
Vậy A chia hết cho 21, 60, 140
A không chia hết 91, 150, 270
Câu 3: Tìm các ước nguyên tố của các số sau:
a) 525
b) 144
c) 180
Lời giải:
a) 525 = 3 . 52 . 7
Vậy các ước nguyên tố của 525 là: 3; 5; 7
b) 144 = 24 . 32
Vậy các ước nguyên tố của 144 là: 2; 3
c) 180 = 22 . 32 . 5
Vậy các ước nguyên tố của 180 là: 2; 3; 5
Câu 4: Số 98 có bao nhiêu ước số?
Lời giải:
Cách 1: Ư(98) = {1; 2; 7; 14; 49; 98}. Vậy số 98 có 6 ước số
Cách 2: Ta có: 98 = 2 . 72
Vậy số ước số của 98 là: (1 + 1) . (2 + 1) = 6 ước
Để tìm số ước của số tự nhiên m (m > 1), ta có thể làm như sau:
Cách 1: Liệt kê rồi đếm các ước của m
Cách 2: Xét dạng phân tích của số m ra thừa số nguyên tố:
• Nếu m = ax thì m có (x + 1) ước
• Nếu m = ax . by thì m có (x + 1)(y + 1) ước
• Nếu m = ax . by . cz thì m có (x + 1)(y + 1)(z + 1) ước
---------------------
Tham khảo thêm: Chuyên đề Toán 6








