Toán lớp 6 - Chuyên đề khi nào thì xOy + yOz = xOz
Chuyên đề khi nào thì xOy + yOz = xOz
Chuyên đề về cộng góc Toán lớp 6 được VnDoc tổng hợp và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 6 hiệu quả hơn. Mời các bạn tham khảo.
Đây là phần bài tập về cộng góc được chia làm hai phần chính: Lý thuyết và Bài tập vận dụng. Phần lý thuyết gồm nhận biết khi nào thì góc xOy + yOz = xOz, hai góc kề nhau, hai góc phụ nhau, bù nhau, kề bù và các dạng bài tập thường gặp có vi dụ đi kèm. Bài tập bao gồm các bài toán nhỏ với câu hỏi trắc nghiệm kèm theo đáp án, lời giải cho một số bài nâng cao. Qua đó sẽ giúp cho các bạn học sinh ôn tập và củng cố lại kiến thức về phần chuyên đề góc đã được học trong chương trình Toán lớp 6 này.
Nội dung của chuyên đề khi nào thì góc xOy + yOz = xOz
A. Lý thuyết
1. Nhận xét
Nếu tia Oy nằm giữa hai tia Ox và Oz thì 
\(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\)
Ngược lại, nếu \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\) thì tia Oy nằm giữa hai tia Ox, Oz
2. Hai góc kề nhau, phụ nhau, bù nhau, kề bù
Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ chứa cạnh chung.
Hai góc phụ nhau là hai góc có tổng số đo bằng 90º, chẳng hạn góc 50º và góc 40° là hai góc phụ nhau.
Hai góc bù nhau là hai góc có tổng số đo bằng 180º
Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.
3. Các dạng toán cơ bản
3.1. Dạng 1: Tính số đo góc
Phương pháp giải: Vận dụng tính chất cộng số đo hai góc.
Ví dụ 1: Cho biết OA nằm giữa hai tia OB, OC, góc BOA = 45º, góc AOC = 32º. Tính góc BOC.
Lời giải:
Vì tia OA nằm giữa hai tia OB và OC nên \(\widehat {BOA} + \widehat {AOC} = \widehat {BOC}\)
Thay số ta tính được góc BOC = 77º
3.2. Dạng 2: Hai góc phụ nhau, bù nhau
Phương pháp giải: Muốn biết hai góc có phụ nhau hay bù nhau không, ta cần xét tổng số đo của hai góc ấy. Nếu tổng bằng 90 độ hay 180 độ thì hai góc đó phụ nhau hay bù nhau.
3.3. Dạng 3: Xác định một tia có nằm giữa hay không nằm giữa hai tia khác nhau
Phương pháp giải: Dùng nhận xét nếu xÔy + yÔz ≠ xÔz thì tia Oy không nằm giữa hai tia Ox và Oz hoặc so sánh hai góc chung cạnh (ví dụ như xÔy, xÔz có xÔy < xÔz thì tia Oy nằm giữa hai tia Ox và Oz)
Ví dụ 2: Cho ba tia chung gốc Ox, Oy, Oz sao cho xÔy = 130 độ; yÔz = 140 độ; xÔz = 90 độ. Trong ba tia này có tia nào nằm giữa hai tia còn lại không?
Lời giải:
Ta thấy xÔy + yÔz ≠ xÔz (vì 130 độ +140 độ ≠ 90 độ) nên tia Oy không nằm giữa hai tia Ox và Oz.
Ta thấy xÔz + zÔy ≠ xÔy (vì 90 độ +140 độ ≠ 130 độ) nên tia Oz không nằm giữa hai tia Ox và Oy.
Ta thấy yÔx + xÔz ≠ yÔz (vì 130 độ + 90 độ ≠ 140 độ) nên tia Ox không nằm giữa hai tia Oy, Oz.
Vậy trong ba tia Ox, Oy, Oz không có tia nào nằm giữa hai tia còn lại.
B. Bài tập vận dụng
1. Trắc nghiệm
Câu 1: Cho ba tia chung gốc Ox, Oy, Oz và \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\). Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại?
| A. Tia Ox | B.Tia Oy | C.Tia Oz | D.Không có |
Câu 2: Cho góc O = 30º. Góc A phụ với góc O. Số đo góc A là
| A. 150º | B.40º | C.60º | D.70º |
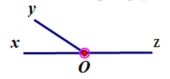
Câu 3: Cho hình vẽ, kể tên các góc kề bù với góc \(\widehat {xOy}\)
| A.\(\widehat {xOy}\) |
B. \(\widehat {xOz}\) |
C. Không có | D. \(\widehat {zOy}\) |
Câu 4: Cho tia Oz nằm giữa hai tia Ox và Oy. Biết \(\widehat {xOz} = 4{0^0}\), \(\widehat {xOy} = 7{0^0}\). Số đo của góc yOz bằng:
| A. 110º | B.40º | C.30º | D.70º |
Câu 5: Cho hai góc xOy và góc yOy’ kề bù với nhau. Biết \(\widehat {xOy} = 12{0^0}\). Tính \(\widehat {y'Oy}\)
| A. 120º | B.60º | C.80º | D.180º |
Câu 6: Cho ba tia chung gốc Ox, Oy, Oz. Biết \(\widehat {xOy} = {65^0}\)và \(\widehat {xOz} = 3{5^0}\). Số đo của góc yOz bằng:
| A. 30º | B.100º | C.125º | D.180º |
Câu 7: Cho hai góc xOy và góc yOy’ kề bù với nhau. Biết \(\widehat {xOy} = 2{0^0}\). Tính \(\widehat {y'Oy}\)
| A. 20º | B.60º | C.80º | D.70º |
Câu 8: Nếu có \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\) thì tia nằm giữa hai tia là
| A. Ox | B.Oz | C.Oy | D.xy |
Câu 9: Nếu tia Oa nằm giữa hai tia Ob và Oc thì
| A.\(\widehat {aOb} + \widehat {bOc} = \widehat {aOc}\) |
B.\(\widehat {aOc} + \widehat {bOc} = \widehat {aOb}\) |
| C.\(\widehat {bOa} + \widehat {aOc} = \widehat {bOc}\) |
D.\(\widehat {aOc} + \widehat {aOc} = \widehat {aOb}\) |
Câu 10: Trên nửa mặt phẳng bờ chứa tia Ox, nếu \(\widehat {xOy} < \widehat {xOz}\) thì tia nằm giữa là:
| A.Ox | B.Oy | C.Oz | D.Không có |
Câu 11: Nếu tia Oy nằm giữa hai tia Ox và Oz và và là góc nhọn thì số đo là
| A. 30º | B.50º | C.90º | D.140º |
Câu 12: Cho hình vẽ. Biết \(\widehat {xOz} = {130^0}\). Hỏi số đo góc \(\widehat {yOz}\) bằng bao nhiêu độ?
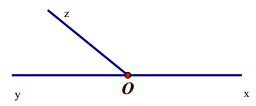
| A. 30º | B.130º | C.90º | D.50º |
Câu 13: Cho hình vẽ. Biết \(\widehat {xOz} = {130^0}\). Hỏi số đo góc \(\widehat {yOx}\) bằng bao nhiêu độ?
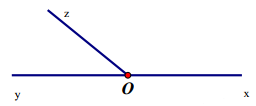
| A. 80º | B.180º | C.90º | D.50º |
Câu 14: Gọi M là điểm nằm giữa hai điểm A và B. Lấy điểm O không nằm trên đoạn thẳng AB, vẽ 3 tia OM, OA, OB. Tia nào nằm giữa 2 tia còn lại.
| A.OM | B.OA | C.OB | D.Không có |
2. Tự luận
Bài 1: Điền vào chỗ trống:
a, Hai góc phụ nhau là hai góc có tổng số đo bằng……….
b, Hai góc bù nhau là hai góc có tổng số đo bằng…………
c, Hai góc vừa kề nhau vừa bù nhau là hai góc…………….
Bài 2: Cho hai đường thẳng AB và CD cắt nhau tại O. Biết \(\widehat {AOC} - \widehat {BOC} = 4{0^0}\). Tính \(\widehat {AOC},\widehat {BOC},\widehat {BOD},\widehat {AOD}\)
Bài 3: Cho \(\widehat {xOy} = 6{0^0}\). Tia Oz nằm trong góc xOy sao cho \(\widehat {xOz} = \frac{1}{3}\widehat {xOy}\). Tính số đo của các góc zOx, zOy.
Bài 4: Cho góc bẹt xOy. Hai điểm A, B nằm về hai phía của đường thẳng xy. Tính số đo các góc AOy, xOB, AOB, biết \(\widehat {xOA} = 12{0^0};\widehat {BOy} = 4{5^0}\)
Bài 5: Hai đường thẳng AB và CD cắt nhau tại O. Chứng minh rằng:
a, \(\widehat {AOC} = \widehat {BOD}\)
b, \(\widehat {AOD} = \widehat {BOC}\)
Bài 6: Trên đường thẳng xy lấy điểm O và kẻ hai tia Oz và Ot trên cùng một nửa mặt phẳng bờ xy. Biết rằng các góc xOz và tOy là hai góc phụ nhau. Gọi Oz’ là tia đối của tia Oz và Ot’ là tia đối của tia Ot. Hỏi góc t’Oz’ là góc gì?
Bài 7: Cho \(\widehat {xOy} = 12{0^0}\)và điểm A trong góc xOy sao cho \(\widehat {yOA} = {75^0}\) và điểm B không nằm trong góc xOy sao cho \(\widehat {xOB} = 13{5^0}\). Chứng tỏ rằng ba điểm A, O, B thẳng hàng.
Bài 8: Cho góc xOy có số đo 90º, vẽ tia Oz sao cho góc yOz bằng 30º
a, Tia Oz có xác định duy nhất không?
b, Tính góc xOz trong từng trường hợp.
Bài 9: Trên cùng một nửa mặt phẳng bờ chứa tia OA, vẽ hai tia OB, OC sao cho \(\widehat {BOA} = 14{5^0}\), \(\widehat {COA} = 5{5^0}\)
a, Tia nào nằm giữa hai tia?
b, Tính số đo \(\widehat {BOC}\)
Bài 10: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ hai tia Oy và Ot sao cho góc \(\widehat {xOy} = {35^0}\)và \(\widehat {xOt} = 7{0^0}\)
a, Tia nào nằm giữa hai tia còn lại? Vì sao?
b, Tính \(\widehat {yOt}\)
Bài 11: Trên cùng nửa mặt phẳng bờ chứa tia OA, vẽ \(\widehat {AOB} = 6{0^0};\widehat {AOC} = {120^0}\)
a, Tia nào nằm giữa hai tia còn lại? Vì sao?
b, Tính \(\widehat {BOC}\)
Bài 12: Trên đường thẳng xy lấy điển O và trên cùng nửa mặt phẳng bờ là xy kẻ 2 tia Oz và Ot sao cho \(\widehat {yOt} = 13{4^0}\)và \(\widehat {xOz} = 13{6^0}\). Tính \(\widehat {tOz}\).
C. Lời giải
| Câu 1 | Câu 2 | Câu 3 | Câu 4 | Câu 5 | Câu 6 | Câu 7 |
| B | C | D | C | B | B | D |
| Câu 8 | Câu 9 | Câu 10 | Câu 11 | Câu 12 | Câu 13 | Câu 14 |
| C | C | B | A | D | B | A |
(Để xem trọn bộ đáp án mời tải tài liệu về)
-------------
Ngoài Chuyên đề về cộng góc; mời các bạn học sinh tham khảo thêm đề cương ôn tập học kì 2 môn Toán hay các đề thi giữa học kì 2 môn Toán, Ngữ Văn như:
- Đề cương ôn tập học kì 2 môn Toán lớp 6 năm học 2019 - 2020
- Bộ đề thi giữa học kì 2 môn Toán lớp 6
- 10 đề thi thử học kì 2 môn Toán lớp 6
- Bộ đề thi giữa học kì 2 môn Ngữ văn lớp 6
mà chúng tôi đã sưu tầm và chọn lọc. Với chuyên đề này sẽ giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tập tốt!
