Ba đường conic trong mặt phẳng tọa độ
1. Định nghĩa
Trong mặt phẳng cho hai điểm cố định 
\(F_1, F_2\) với \(F_1F_2 = 2c\) và một độ dài không đổi \(2a\) \((0 < c < a)\). Elip \((E)\) là tập hơp tất cả các điểm M trong mặt phẳng thỏa mãn \(MF_1 + MF_2 = 2a\). Ta gọi:
\(F_1, F_2\): Tiêu điểm của elip.
\(F_1F_2 = 2c\): Tiêu cự của elip.
\(MF_1, MF_2\): Bán kính qua tiêu
Hình vẽ minh họa
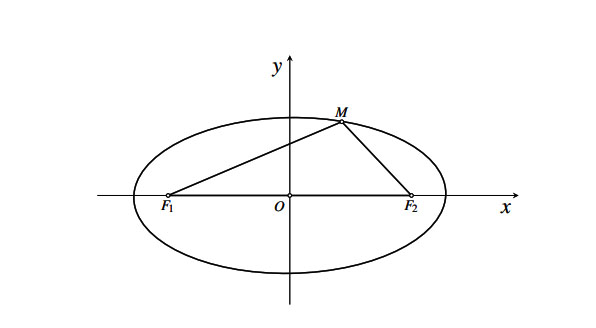
2. Phương trình chính tắc của elip
Phương trình chính tắc của elip
\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Trong đó \({a^2} = {b^2} + {c^2}\).
3. Hình dạng của elip
Hình vẽ minh họa
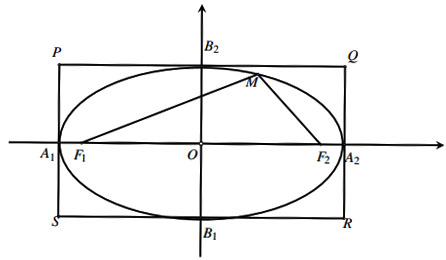
a) Trục đối xứng của elip
Elip có phương trình \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) nhận các trục tọa độ làm trục đối xứng và nhận gốc tọa độ làm tâm đối xứng.
b) Hình chữ nhật cơ sở
Vẽ qua \(A_1\) và \(A_2\) hai đường thẳng song song với trục tung, vẽ qua \(B_1\) và \(B_2\) hai đường thẳng song song với trục hoành. Bốn đường thẳng đó tạo thành hình chữ nhật \(PQRS\).
Ta gọi hình chữ nhật đó là hình chữ nhật cơ sở của elip.
Từ đó suy ra:
- Mọi điểm của elip nếu không phải là đỉnh đều nằm trong hình chữ nhật cơ sở của nó, bốn đỉnh của elip là trung điểm các cạnh của hình chữ nhật cơ sở.
- Các điểm: \(A_1(−a; 0); A_2(a; 0); B_1(0;−b); B_2(0;b)\) gọi là các đỉnh của elip.
- \(A_1A_2 = 2a\): Độ dài trục lớn.
- \(B_1B_2 = 2b\): Độ dài trục bé.
c) Tâm sai của elip
Tỉ số giữa tiêu cự và độ dài trục lớn của elip gọi là tâm sai của elip và được kí hiệu là \(e\) tức là \(e = \frac{c}{a}\).
- Nếu tâm sai \(e\) càng bé (tức là càng gần \(0\)) thì \(b\) càng gần \(a\) và hình chữ nhật cơ sở càng gần với hình vuông, do đó đường elip càng “béo”.
- Nếu tâm sai \(e\) càng lớn (tức là càng gần \(1\)) thì tỉ số \(\frac{b}{a}\) càng gần tới \(1\) và hình chữ nhật cơ sở càng “dẹt”, do đó đường elip càng “gầy”.
Ví dụ: Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\). Tìm các tiêu điểm và tiêu cự của elip. Tính tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm.
Hướng dẫn giải
Ta có: \(a^2 = 25, b^2 = 16\). Do đó \(c = \sqrt {{a^2} - {b^2}} = 3\).
Vậy elip có hai tiêu điểm là \({F_1}\left( { - 3;0} \right);{F_2}\left( {3;0} \right)\) và tiêu cự là \({F_1}{F_2} = 2c = 6\).
Ta có \(a = \sqrt {25} = 5\), nên tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm bằng \(2a= 10\).
B. Hypebol
Định nghĩa
Cho hai điểm \(F_1, F_2\) và một độ dài không đổi \(2a\) nhỏ hơn \(F_1F_2\) Hypebol là tập hợp các điểm M trong mặt phẳng sao cho \(\left| {{F_1}M - {F_2}M} \right| = 2a\).
Các điểm \(F_1, F_2\) gọi là các tiêu điểm của hypebol.
Độ dài \(F_1F_2 = 2c\) gọi là tiêu cự của hypebol (\(c> a\)).
Hình vẽ minh họa
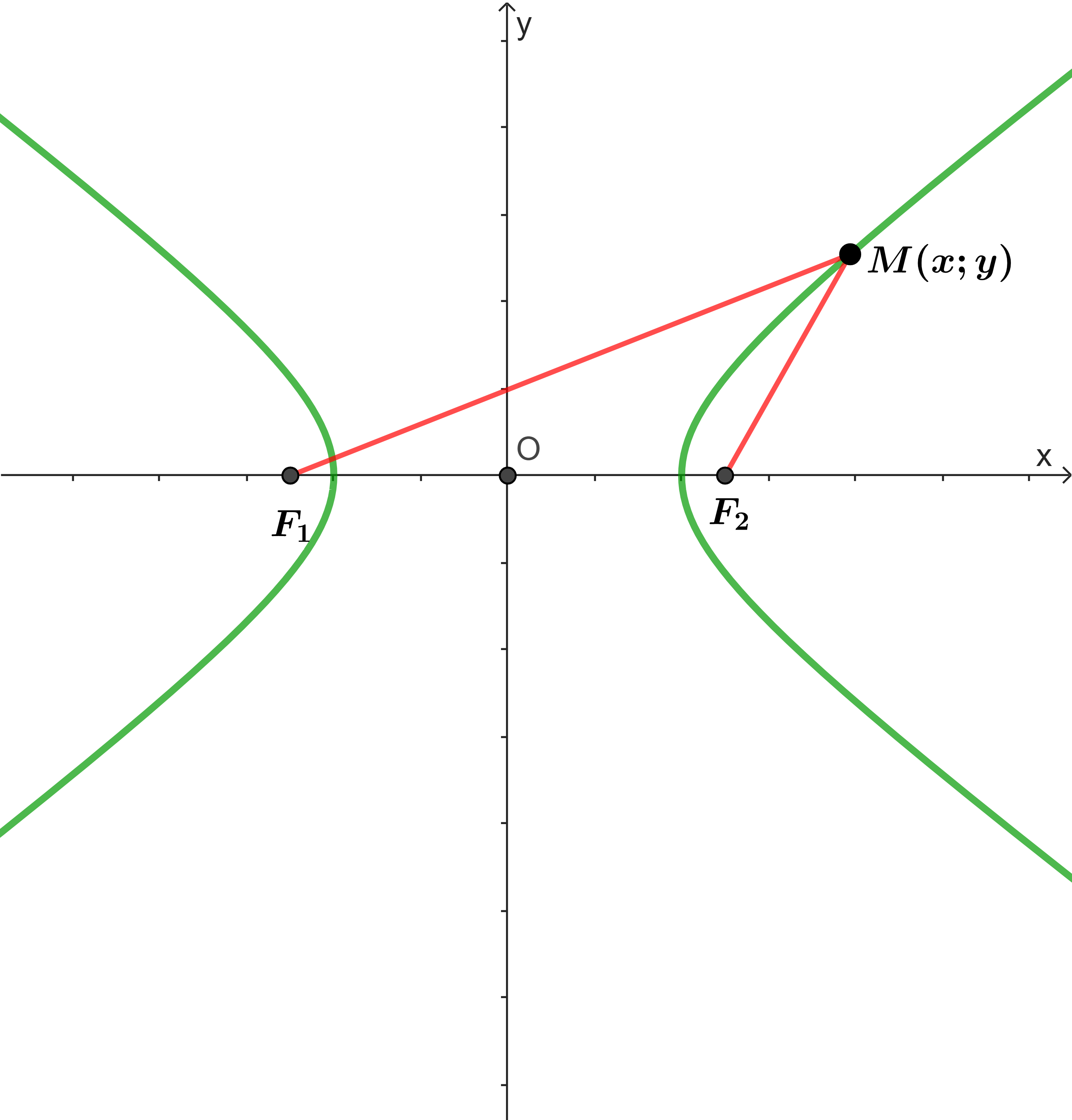
Phương trình chính tắc của hypebol
Phương trình chính tắc của hypebol
\(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Trong đó \({a^2} = {b^2} + {c^2}\).
Hình vẽ minh họa
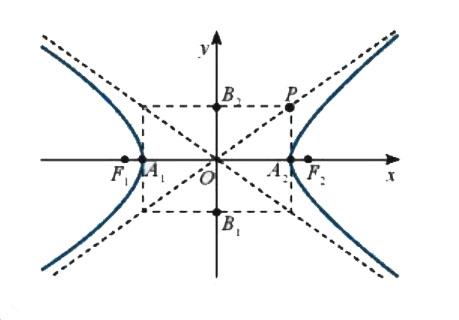
Chú ý
- \((H)\) cắt Ox tại hai điểm \(A_1(-a, 0)\) và \(A_2(a, 0)\). Nếu vẽ hai điểm \(B_1(-b, 0)\) và \(B_2(b, 0)\) vào hình chữ nhật \(OA_2PB_2\) thì \(OP = \sqrt {{a^2} + {b^2}} = c\)
- Các điểm \(A_1, A_2\) gọi là các đỉnh của hypebol.
- Đoạn thẳng \(A_1A_2\) là trục thực.
- Đoạn thẳng \(B_1B_2\) là trục ảo.
- Giao điểm \(B_1B_2\) của hai trục gọi là tâm đối xứng của hypebol.
- Nếu \(M\left( {x,y} \right) \in \left( H \right)\) thì \(\left[ {\begin{array}{*{20}{c}}
{x \leqslant - a} \\
{x \geqslant a}
\end{array}} \right.\)
Ví dụ: Cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\). Tìm các tiêu điểm và tiêu cự của hypebol. Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?
Hướng dẫn giải
Ta có \({a^2} = 9,{b^2} = 16\) nên \(c = \sqrt {{a^2} + {b^2}} = 5\).
Vậy hypebol có hai tiêu điểm là \({F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)\) và có tiêu cự \(2c = 10\).
Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng \(2{\rm{a}} = 2\sqrt 9 = 6\).
C. Parabol
Định nghĩa
Cho một điểm \(F\) và đường thẳng \(∆\) cố định không đi qua \(F\). Parabol \((P)\) là tập hợp các điểm cách đều \(F\) và \(∆\).
\(F\) gọi là tiêu điểm và \(∆\) gọi là đường chuẩn của parabol.
Phương trình chính tắc của parabol
Gọi p là khoảng cách từ tiêu điểm đến đường chuẩn là p
Phương trình chính tắc của parabol:
\({y^2} = 2px\)
Chú ý
O là đỉnh của \((P)\)
Ox là trục đối xứng của \((P)\)
p gọi là tham số tiêu của parabol \((P)\)
Nếu \(M\left( {x,y} \right) \in \left( P \right)\) thì \(\left\{ {\begin{array}{*{20}{c}}
{x \geqslant 0} \\
{M'\left( {x, - y} \right) \in \left( P \right)}
\end{array}} \right.\)
Ví dụ: Cho parabol \((P)\): \({y^2} = x\).
a) Tìm tiêu điểm \(F\), đường chuẩn \(\Delta\) của \((P)\).
b) Tìm những điểm trên \((P)\) có khoảng cách tới \(F\) bằng 3.
Hướng dẫn giải
a) Ta có \(2p = 1\) nên p = \(\frac{1}{2}\).
Parabol có tiêu điểm \(F\left( {\frac{1}{4};0} \right)\) và đường chuẩn \(\Delta :x = - \frac{1}{4}\)
b) Điểm \(M\left( {{x_0};{y_0}} \right)\) thuộc \((P)\) có khoảng các tới \(F\) bằng 3 khi và chỉ khi \({y_0}^2 = {x_0}\) và MF = 3.
Do \(MF=d\left( {M,\Delta } \right)\) nên \(d\left( {M,\Delta } \right) = 3\)
Mặt khác \(\Delta :x + \frac{1}{4} = 0\) và \({x_0} = {y_0}^2 \ge 0\) nên \(3 = d\left( {M,\Delta } \right) = \left| {{x_0} + \frac{1}{4}} \right| = {x_0} + \frac{1}{4}\).
Vậy \({x_0} = \frac{{11}}{4},{y_0} = \frac{{\sqrt {11} }}{2},{y_0} = - \frac{{\sqrt {11} }}{2}\).
Vậy có hai điểm \(M\) thoả mãn bài toán với toạ độ là \(\left( {\frac{{11}}{4};\frac{{\sqrt {11} }}{2}} \right) và \left( {\frac{{11}}{4}; - \frac{{\sqrt {11} }}{2}} \right)\).
