Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 10 Khóa học Lớp 10 Toán 10 - Chân trời sáng tạo

Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 4

Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ
Mô tả thêm:

Cùng nhau ôn tập, thử sức với Đề kiểm tra học kì 2 Toán 10 - Chân trời sáng tạo nha!
  • Thời gian làm: 90 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Bắt đầu làm bài
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé!
Mua ngay Đổi điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
  • Câu 1: Thông hiểu

    Tìm phương trình đường tròn

    Cho hai đường thẳng \left( d_{1} ight):x + 3y + 8 = 0; \left( d_{2} ight):3x - 4y + 10 = 0 và điểm A( - 2;1). Phương trình đường tròn có tâm I \in \left( d_{1} ight), đi qua điểm A và tiếp xúc với \left( d_{2} ight) là:

    Hình vẽ minh họa

    Ta có I là tâm đường tròn và I \in \left( d_{1} ight) nên I( - 3t - 8;t)

    Theo giả thiết bài toán ta có:

    d\left( I;\left( d_{2} ight) ight) = IA

    \Leftrightarrow \frac{\left| 3( - 3t - 8) - 4t + 10 ight|}{\sqrt{3^{2} + 4^{2}}} = \sqrt{( - 3t - 8 + 2)^{2} + (t - 1)^{2}}

    \Leftrightarrow t = - 3

    Suy ra I(1; - 3) và bán kính R = IA = 5

    Vậy phương trình đường tròn cần tìm là: (C):(x - 1)^{2} + (y + 3)^{2} = 25.

  • Câu 2: Nhận biết

    Tìm độ dài đường kính

    Cho đường tròn (C):x^{2}+y^{2}+4x+4y-17=0 , hỏi độ dài đường kính bằng bao nhiêu?

     Ta có tâm I( - 2; - 2). Suy ra bán kính R = \sqrt {{{( - 2)}^2} + {{( - 2)}^2} + 17} = 5.

    Do đó đường kính bằng 10.

  • Câu 3: Nhận biết

    Xác suất để 4 quân bài đều là Át

    Một người chọn ngẫu nhiên đồng thời 4 quân bài từ bộ tú lơ khơ 52 quân bài. Tính xác suất của biến cố: “Cả 4 quân bài đều là Át”?

    Số phần tử không gian mẫu: n(\Omega) = C_{52}^{4}

    Chỉ có đúng 1 cách để lấy được cả 4 quân bài đều là Át nên xác suất cần tìm là:

    P = \frac{1}{C_{52}^{4}}

  • Câu 4: Thông hiểu

    Chọn đáp án đúng

    Trên bàn có 4 quyển sách toán, 3 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để trong ba quyển sách lấy ra có ít nhất một quyển là toán?

    Xác suất để trong ba quyển lấy ra có ít nhất một quyển sách Toán là: 1 - \frac{C_{3}^{3}}{C_{7}^{3}} = \frac{34}{35}

  • Câu 5: Nhận biết

    Tính khoảng cách từ A đến đường thẳng d

    Trong mặt phẳng Oxy cho điểm A(4; - 5) và đường thẳng (d):3.x - 4y + 8 = 0. Tính khoảng cách từ điểm A đến đường thẳng (d).

    Khoảng cách từ điểm A đến đường thẳng (d) là:

    d\left( A;(d) ight) = \frac{\left| 3.4 - 4.( - 5) + 8 ight|}{\sqrt{3^{2} + 4^{2}}} = 8

    Vậy khoảng cách cần tìm bằng 8.

  • Câu 6: Thông hiểu

    Tính xác suất lấy được 3 sản phẩm đạt chuẩn

    Một lô sản phẩm gồm 35 sản phẩm đạt chuẩn và 15 sản phẩm lỗi. Lấy ngẫu nhiên 3 sản phẩm từ trong hộp. Tính xác suất để 3 sản phẩm lấy ra đều là sản phẩm đạt chuẩn?

    Ta có: n(\Omega) = C_{50}^{3}

    Gọi B là biến cố cả ba sản phẩm lấy ra đều là sản phẩm đạt chuẩn.

    Chọn 3 trong 35 sản phẩm đạt chuẩn ta có: \Rightarrow n(B) = C_{35}^{3}

    Vậy xác suất của biến cố B là: P(B) = \frac{C_{35}^{3}}{C_{50}^{3}} = \frac{187}{560}.

  • Câu 7: Thông hiểu

    Tìm điểm thỏa mãn điều kiện

    Trong mặt phẳng Oxy, cho Parabol (P): y^{2} = 8x có tiêu điểm F. Tìm trên (P) điểm M cách F một khoảng là 3.

    Giả sử M\left( x_{M}\ ;\ y_{M} ight) \in (P). Suy ra {y_{M}}^{2} = 8x_{M}. (1)

    Từ phương trình y^{2} = 8x suy ra p = 4 nên F(2\ ;\ 0).

    Ta có: FM = \frac{p}{2} + x_{M}. Suy ra x_{M} = 1. Kết hợp (1) ta có: y_{M} = \pm 2\sqrt{2}.

    Vậy có hai điểm M\left( 1\ ;\ 2\sqrt{2} ight) hoặc M\left( 1\ ;\ - 2\sqrt{2} ight)thỏa mãn.

  • Câu 8: Nhận biết

    Tổng các bình phương của các nghiệm là

    Tổng các bình phương của các nghiệm của phương trình(x - 1)(x - 3) + 3\sqrt{x^{2} - 4x + 5} - 2 = 0 bằng bao nhiêu?

    Ta có (x - 1)(x - 3) + 3\sqrt{x^{2} - 4x + 5} - 2 = 0

    \Leftrightarrow x^{2} - 4x + 5 +3\sqrt{x^{2} - 4x + 5} - 4 = 0\Leftrightarrow \sqrt{x^{2} - 4x + 5} =1

    \Leftrightarrow x^{2} - 4x + 5 = 1 \Leftrightarrow x^{2} - 4x + 4 = 0 \Leftrightarrow x = 2.

    Tổng các bình phương của các nghiệm của phương trình là 4.

  • Câu 9: Vận dụng cao

    Tính giá trị nhỏ nhất của biểu thức

    Trong mặt phẳng tọa độ Oxy, cho tọa độ hai điểm A( - 1;5),B(5;3) và đường thẳng (\Delta):3x + 4y - 12 = 0. Lấy một điểm H bất kì trên đường thẳng (\Delta). Khi đó biểu thức \left| \overrightarrow{HA} + \overrightarrow{HB}ight| đạt giá trị nhỏ nhất bằng:

    Gọi I là trung điểm của AB khi đó I(2; 4)

    Ta có:

    \left| \overrightarrow{HA} +\overrightarrow{HB} ight| = \left| \overrightarrow{HI} +\overrightarrow{IA} + \overrightarrow{HI} + \overrightarrow{IB}ight|

    = \left| 2\overrightarrow{HI} + \left(\overrightarrow{IA} + \overrightarrow{IB} ight) ight| =2HI

    Nên \left| \overrightarrow{HA} +\overrightarrow{HB} ight|_{\min} khi HI_{\min}khi và chỉ khi H là hình chiếu vuông góc của I lên đường thẳng (\Delta)

    Khi đó: HI = d(I;\Delta) = \frac{|3.2 +4.4 - 12|}{\sqrt{3^{3} + 4^{2}}} = 2

    Vậy biểu thức \left| \overrightarrow{HA}+ \overrightarrow{HB} ight| đạt giá trị nhỏ nhất bằng 2.

  • Câu 10: Nhận biết

    Tìm vectơ chỉ phương

    Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A(– 3; 2) và B(1; 4).

     Vectơ chỉ phương của đường thẳng AB là (2; 1).

  • Câu 11: Thông hiểu

    Hỏi có thể lập được bao nhiêu số

    Từ các chữ số 0, 2, 3, 5, 6, 8 có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số đôi một khác nhau trong đó hai chữ số 0 và 5 không đứng cạnh nhau.

    Số các số có 6 chữ số được lập từ các chữ số 0, 2, 3, 5, 6, 8 là 6! - 5!.

    Số các số có chữ số 0 và 5 đứng cạnh nhau: 2.5! - 4!.

    Số các số có chữ số 0 và 5 không đúng cạnh nhau là: 6! - 5! - (2.5! - 4!) = 384.

  • Câu 12: Vận dụng

    Xác suất để lấy các viên bi có cùng màu

    Cho biết:

    Hộp 1: chứa 4 viên bi đỏ và 3 viên bi xanh.

    Hộp 2: chứa 5 viên bi đỏ và 2 viên bi xanh.

    Lấy ngẫu nhiên từ mỗi hộp 2 viên bi. Xác suất để lấy các viên bi có cùng màu bằng:

    Lấy ngẫu nhiên 2 viên bi từ hộp 1 ta có: C_{7}^{2} = 21

    Lấy ngẫu nhiên 2 viên bi từ hộp 2 ta có: C_{7}^{2} = 21

    Ta có số phần tử không gian mẫu là: n(\Omega) = 21.21 = 441

    Gọi A là biến cố các viên bi lấy ra cùng màu.

    Số phần tử của biến cố A là: n(A) = C_{4}^{2}.C_{5}^{2} + C_{3}^{2}.C_{2}^{2}

    Vậy xác suất cần tìm là: P(A) = \frac{n(A)}{n(\Omega)} = \frac{1}{7}

  • Câu 13: Thông hiểu

    Viết phương trình tổng quát của đường thẳng

    Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1;2),B(2; - 1),C(0;1). Phương trình đường thẳng chứa trung tuyến kẻ từ đỉnh B của tam giác ABC là:

    Gọi I là trung điểm của AC. Ta có: I\left( \frac{1}{2};\frac{3}{2} ight)

    Đường trung tuyến BI đi qua điểm B và nhận \overrightarrow{BI} = \left( - \frac{3}{2};\frac{5}{2} ight) làm vectơ chỉ phương nên có vectơ pháp tuyến \overrightarrow{n} = (5;3).

    Phương trình tổng quát của đường thẳng BI là:

    5(x - 2) + 3(y + 1) = 0

    \Leftrightarrow 5x + 3y - 7 = 0

    Vậy phương trình tổng quát của đường thẳng cần tìm là 5x + 3y - 7 = 0.

  • Câu 14: Nhận biết

    Định khai triển chính xác

    Khai triển biểu thức \left( x^{2} - 5y ight)^{5} ta được:

    Ta có:

    \left( x^{2} - 5y ight)^{5}

    = C_{5}^{0}.\left( x^{2} ight)^{5} + C_{5}^{1}\left( x^{2} ight)^{4}.( - 5y) + C_{5}^{2}.\left( x^{2} ight)^{3}.( - 5y)^{2}

    + C_{5}^{3}.\left( x^{2} ight)^{2}.( - 5y)^{3} + C_{5}^{4}.\left( x^{2} ight)^{1}.( - 5y)^{4} + C_{5}^{5}.\left( x^{2} ight)^{0}.( - 5y)^{5}

    =x^{10} - 25x^{8}y + 250x^{6}y^{2} -1250x^{4}y^{3} + 3125x^{2}y^{4} - 3125y^{5}

  • Câu 15: Thông hiểu

    Chọn đáp án đúng

    Cho tập hợp C = \left\{ 1;3;5;7 ight\} có thể lập được bao nhiêu số tự nhiên có 4 chữ số?

    Gọi số tự nhiên có 4 chữ số cần tìm là \overline{abcd},(a eq 0).

    Số cách chọn a là 4 cách

    Số cách chọn b là 4 cách

    Số cách chọn c là 4 cách

    Số cách chọn d là 4 cách

    Vậy số các số tự nhiên có 4 chữ số có thể lập được là 4^{4} = 256.

  • Câu 16: Nhận biết

    Tìm phương trình đường tròn

    Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?

    Xét phương trình dạng : x^{2} + y^{2} - 2ax - 2by + c = 0, lần lượt tính các hệ số a,\ b,\ c và kiểm tra điều kiện a^{2} + b^{2} - c > 0.

    x^{2} + y^{2} - 4x + 6y - 12 = 0 ightarrow a = 2,\ b = - 3,\ c = - 12 ightarrow a^{2} + b^{2} - c > 0.

    Các phương trình 4x^{2} + y^{2} - 10x - 6y - 2 = 0,\ \ x^{2} + 2y^{2} - 4x - 8y + 1 = 0 không có dạng đã nêu loại các đáp án 4x^{2} + y^{2} - 10x - 6y - 2 = 0 và x^{2} + 2y^{2} - 4x - 8y + 1 = 0.

    Đáp án x^{2} + y^{2} - 2x - 8y + 20 = 0 không thỏa mãn điều kiện a^{2} + b^{2} - c > 0.

  • Câu 17: Thông hiểu

    Tìm nghiệm của phương trình

    Nghiệm của phương trình \frac{x^{2}-4x+3}{\sqrt{x-1}}=\sqrt{x-1} là:

     Điều kiện: x>1.

    Ta có: \frac{x^{2}-4x+3}{\sqrt{x-1}}=\sqrt{x-1} \Rightarrow x^2-4x+3=x-1\Leftrightarrow x^2-5x+4=0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = 4}\end{array}} ight..

    Loại x=1. Do đó S=\{4\}.

  • Câu 18: Thông hiểu

    Viết phương trình tiếp tuyến của đường tròn

    Trong mặt phẳng tọa độ Oxy, cho đường tròn (C):(x + 3)^{2} + (y - 5)^{2} = 10. Viết phương trình tiếp tuyến của đường tròn đã cho, biết hệ số góc của tiếp tuyền bằng - \frac{1}{3}.

    Đường tròn (C) có tâm I( - 3;5) và bán kính R = \sqrt{10}

    Tiếp tuyến d có hệ số góc k = - \frac{1}{3} nên có dạng y = - \frac{1}{3}x + b

    \Leftrightarrow x + 3y - 3b = 0

    Vì d là tiếp tuyến của (C) nên d(I;d) = R

    \Leftrightarrow \frac{| - 3 + 3.5 - 3b|}{\sqrt{1^{2} + 3^{2}}} = \sqrt{10}

    \Leftrightarrow |12 - 3b| = 10\Leftrightarrow \left\lbrack \begin{matrix}b = \dfrac{2}{3} \\b = \dfrac{22}{3} \\\end{matrix} ight.

    Với b = \frac{2}{3} thì phương trình d là: y = - \frac{1}{3}x + \frac{2}{3} \Rightarrow x + 3y - 2 = 0

    Với b = \frac{22}{3} thì phương trình d là: y = - \frac{1}{3}x + \frac{22}{3} \Rightarrow x + 3y - 22 = 0

    Vậy các phương trình tiếp tuyến cần tìm là: x + 3y - 2 = 0;x + 3y - 22 = 0.

  • Câu 19: Nhận biết

    Tìm tiêu cự trục lớn

    Cho hình elip có phương trình \frac{x^{2}}{64} + \frac{y^{2}}{36} = 1. Hình elip có tiêu cự trục lớn bằng:

    Ta có: \frac{x^{2}}{64} + \frac{y^{2}}{36} = 1 \Rightarrow \left\{ \begin{matrix} a = 8 \\ b = 6 \\ \end{matrix} ight.

    Độ dài trục lớn là: 2a = 2.8 = 16

  • Câu 20: Vận dụng

    Nghiệm của phương trình thuộc khoảng nào?

    Phương trình \sqrt[3]{\frac{2x}{x + 1}} + \sqrt[3]{\frac{1}{2} +\frac{1}{2x}} = 2 có nghiệm thuộc khoảng:

    Đặt t = \sqrt[3]{\frac{2x}{x +1}}. Phương trình đã cho trở thành: t+ \frac{1}{t} = 2 \Leftrightarrow t = 1

    Ta được \sqrt[3]{\frac{2x}{x + 1}} = 1\Leftrightarrow x = 1 thuộc [1 ; 2).

  • Câu 21: Nhận biết

    Điền vào chỗ trống

    Điền vào chỗ trống: Vectơ có giá song song hoặc trùng với đường thẳng thì vectơ được gọi là … của đường thẳng đó.

    Vectơ \overrightarrow u có giá song song hoặc trùng với đường thẳng thì \overrightarrow u được gọi là vectơ chỉ phương của đường thẳng đó.

  • Câu 22: Thông hiểu

    Tìm m để ba đường thẳng đồng quy

    Cho ba đường thẳng \left( d_{1} ight):3x + 2y - 5 = 0, \left( d_{2} ight): - 2x + 3y - 1 = 0 và \left( d_{3} ight):(m - 1)x + (2m - 3)y - 2 = 0 với m là tham số. Xác định giá trị của tham số m để ba đường thẳng \left( d_{1} ight);\left( d_{2} ight);\left( d_{3} ight) đồng quy?

    Gọi A = d_{1} \cap d_{2}. Khi đó tọa độ điểm A là nghiệm của hệ phương trình:

    \left\{ \begin{matrix} 3x + 2y - 5 = 0 \\ - 2x + 3y - 1 = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x = 1 \\ y = 1 \\ \end{matrix} ight.\ \Rightarrow A(1;1)

    Để ba đường thẳng đồng quy thì A \in \left( d_{3} ight) hay

    (m - 1).1 + (2m - 3).1 - 2 = 0

    \Leftrightarrow m = 2

    Vậy m = 2 thì ba đường thẳng đã cho đồng quy.

  • Câu 23: Nhận biết

    Biểu diễn biến cố X

    Gieo một đồng xu cân đối liên tiếp bốn lần. Gọi X là biến cố “Kết quả bốn lần gieo là như nhau”. Xác định biến cố X?

    Vì X là biến cố “Kết quả bốn lần gieo là như nhau” nên ta xác định được biến cố như sau: X = \left\{ SSSS;NNNN ight\}

  • Câu 24: Vận dụng

    Tìm tập xác định

    Tìm tập xác định của hàm số y = \frac{2x + 3m}{\sqrt{x^{2} + 2(1 - m)x + 2m^{2} + 3}}.

    ĐKXĐ: x2 + 2(1−m)x + 2m2 + 3 > 0

    Xét tam thức bậc hai f(x) = x2 + 2(1−m)x + 2m2 + 3

    Ta có \begin{matrix} a = 1 > 0,\ \ \Delta' = (1 - m)^{2} - \left( 2m^{2} + 3 ight) \\ = - m^{2} - 2m - 2 < 0 \\ \end{matrix}

    (Vì tam thức bậc hai f(m) =  − m2 − 2m − 2 có am =  − 1 < 0,  Δ′m =  − 1 < 0 )

    Suy ra với mọi m ta có x2 + 2(1−m)x + 2m2 + 3 > 0,  ∀x ∈ ℝ.

    Vậy tập xác định của hàm số là D = ℝ.

  • Câu 25: Thông hiểu

    Tính xác suất của biến cố B

    Một hộp có 5 quả cầu được đánh số từ 1 đến 5 (hai quả cầu khác nhau thì đánh số khác nhau). Lấy ngẫu nhiên liên tiếp 2 quả cầu. Tính xác suất của biến cố B: “Tích các số trên hai quả cầu là số chẵn”?

    Ta có không gian mẫu:

    \Omega = \{(1;2),(1;3),(1;4),(1;5),(2;3),

    (2;4),(2;5),(3;4),(3;5),(4;5)\}

    \Rightarrow n(\Omega) = 10

    Biểu diễn biến cố B là:

    B = \left\{ (1;2),(1;4),(2;3),(2;4),(2;5),(3;4),(4;5) ight\}

    \Rightarrow n(B) = 7

    Vậy xác suất của biến cố B cần tìm là: P(B) = \frac{n(B)}{n(\Omega)} = \frac{7}{10}

  • Câu 26: Nhận biết

    Tìm x thỏa mãn

    Cho tam thức bậc hai f(x) = 5x − x2 − 6. Tìm x để f(x) ≥ 0.

    f(x) = 5x - x^{2} - 6 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 2 \\ x = 3 \\ \end{matrix} ight.

    Dựa vào bảng xét dấu, ta chọn đáp án x ∈ [2; 3].

  • Câu 27: Thông hiểu

    Chọn khẳng định đúng

    Cho hàm số y = f(x) có đồ thị như hình vẽ. Hãy so sánh f(2017) với số 0.

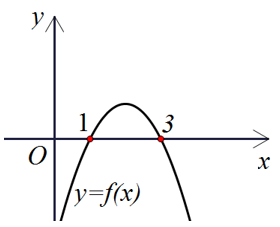
    Nhìn đồ thị, ta thấy đồ thị y = f(x) cắt trục hoành tại 2 điểm x = 1, x = 3 nên Δ > 0, dựa vào hình dạng parabol nên suy ra a < 0 và ta có bảng xét dấu như sau:

    Dựa vào bảng xét dấu thì f(x) < 0 khi x < 1 ∨ x > 3. Mà 2017 > 3 nên f(2017) < 0.

  • Câu 28: Nhận biết

    Giải phương trình

    Số nghiệm của phương trình \sqrt{2x-4}=\sqrt{x^{2}-3x} là:

    Điều kiện: \left\{ {\begin{array}{*{20}{c}} {2x - 4 \geqslant 0} \\ {{x^2} - 3x \geqslant 0} \end{array}} ight.

    \begin{matrix} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \geqslant 2} \\ {x \in \left( { - \infty ;0} ight] \cup \left[ {3; + \infty } ight)} \end{array}} ight. \hfill \\ \Leftrightarrow x \geqslant 3 \hfill \\ \end{matrix}

    \begin{matrix} \sqrt {2x - 4} = \sqrt {{x^2} - 3x} \hfill \\ \Leftrightarrow 2x - 4 = {x^2} - 3x \hfill \\ \Leftrightarrow {x^2} - 5x + 4 = 0 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 1\left( {ktm} ight)} \\ {x = 4\left( {tm} ight)} \end{array}} ight. \hfill \\ \end{matrix}

    Vậy phương trình đã cho có tất cả 1 nghiệm.

  • Câu 29: Nhận biết

    Tính số thực đơn có thể

    Trong menu của một nhà hàng gồm 5 món mặn, 5 món tráng miệng và 3 loại nước uống. Thực khách đến ăn sẽ được lên thực đơn gồm 1 món mặn, 1 món tráng miệng và 1 loại nước uống. Số thực đơn có thể có là:

    Chọn món mặn có 5 cách chọn.

    Số cách chọn món tráng miệng là 5 cách.

    Số cách chọn một loại nước uống là 3 cách.

    Theo quy tắc nhân ta có: 5.5.3 = 75 (cách).

  • Câu 30: Nhận biết

    Chọn khẳng định đúng

    Cho parabol (P):y = 2x^{2} + x - 3. Giao điểm của (P) với trục hoành tại hai điểm A\left( x_{1};y_{1} ight),B\left( x_{2};y_{2} ight). Khẳng định nào sau đây đúng?

    Phương trình hoành độ giao điểm là nghiệm của phương trình:

    2x^{2} + x - 3 = 0

    Áp dụng định lí Vi – et ta có:

    x_{1} + x_{2} = - \frac{b}{a} = - \frac{1}{2}

  • Câu 31: Vận dụng

    Tìm số hạng không chứa x

    Cho biểu thức P = \left( \frac{x + 1}{\sqrt[3]{x^{2}} - \sqrt[3]{x} + 1} - \frac{x - 1}{x - \sqrt{x}} ight)^{10} với x > 0, x eq 1. Số hạng không chứa x trong khai triển Niu-tơn của P là:

    Ta có \frac{x + 1}{\sqrt[3]{x^{2}} - \sqrt[3]{x} + 1} - \frac{x - 1}{x - \sqrt{x}} = \sqrt[3]{x} + 1 - \frac{\sqrt{x} + 1}{\sqrt{x}} = \sqrt[3]{x} - \frac{1}{\sqrt{x}}.

    Nên P = \left( \frac{x + 1}{\sqrt[3]{x^{2}} - \sqrt[3]{x} + 1} - \frac{x - 1}{x - \sqrt{x}} ight)^{10} = \left( \sqrt[3]{x} - \frac{1}{\sqrt{x}} ight)^{10}.

    Số hạng tổng quát của khai triển là: C_{10}^{k}x^{\frac{10 - k}{3}}.\left( \frac{- 1}{\sqrt{x}} ight)^{k} = ( - 1)^{k}C_{10}^{k}x^{\frac{20 - 5k}{6}}.

    Khi k = 4 thì số hạng không chứa x là ( - 1)^{4}C_{10}^{4} = 210.

  • Câu 32: Nhận biết

    Tính số tập hợp con

    Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là:

    Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là tổ hợp chập 3 của 7 phần từ.

    => Số tập hợp con là: C_{7}^{3} tập hợp

  • Câu 33: Thông hiểu

    Xác suất hai bi được chọn đều mang số lẻ

    Trong một hộp chứa một số bi, mỗi bi mang một số từ 1 đến 21 và không có hai bi nào mang số giống nhau. Chọn ngẫu nhiên từ hộp đó ra 2 bi. Xác suất hai bi được chọn đều mang số lẻ là:

    Số cách chọn 2 bi từ 21 bi là: C_{21}^{2}

    Từ số 1 đến 21 có 11 số lẻ nên số cách chọn được 2 viên bi đều mang số lẻ là: C_{11}^{2}

    Vậy xác suất để hai viên bi đều ghi số lẻ là: \frac{C_{11}^{2}}{C_{21}^{2}} = \frac{11}{42}

  • Câu 34: Nhận biết

    Tìm mệnh đề đúng

    Cho A là biến cố liên quan đến phép thử có không gian mẫu \Omega. Tìm mệnh đề đúng.

    Theo định nghĩa xác suất cổ điển, cho phép thử T có không gian mẫu \Omega. Giả thiết rằng các kết quả có thể của T là đồng khả năng, khi đó cho A là biến cố có liên quan đến phép thử có không gian mẫu \Omega. Thì xác suất của biến cố A được tính bởi công thức P(A) = \frac{n(A)}{n(\Omega)}, trong đó n(A);n(\Omega) tương ứng là số phần tử của biến cố A và của không gian mẫu.

  • Câu 35: Vận dụng

    Tìm điều kiện của tham số a thỏa mãn yêu cầu

    Cho đường thẳng (\Delta):x + (a - 1)y - a = 0 và đường tròn (C):x^{2} + y^{2} - 2x + 4y + 2 = 0. Tìm điều kiện của tham số a để (d) tiếp xúc với (C)?

    Đường tròn (C) có tâm I(1; - 2) và bán kính R = \sqrt{1^{2} + 2^{2} - 2} = \sqrt{3}

    Để đường thẳng (\Delta)là tiếp tuyến của đường tròn (C) thì

    d(I;\Delta) = R \Leftrightarrow \frac{\left| 1 - 2(a - 1) - a ight|}{\sqrt{1 + (a - 1)^{2}}} = \sqrt{3}

    \Leftrightarrow \frac{|3 - 3a|}{\sqrt{a^{2} - 2a + 2}} = \sqrt{3}

    \Leftrightarrow |3 - 3a| = \sqrt{3}.\sqrt{a^{2} - 2a + 2}

    \Leftrightarrow (3 - 3a)^{2} = 3a^{2} - 6a + 6

    \Leftrightarrow 2a^{2} - 4a + 1 = 0\Leftrightarrow \left\lbrack \begin{matrix}a = 1 + \dfrac{1}{\sqrt{2}} \\a = 1 - \dfrac{1}{\sqrt{2}} \\\end{matrix} ight.

    Vậy a = 1 \pm \frac{1}{\sqrt{2}} thỏa mãn yêu cầu bài toán.

  • Câu 36: Thông hiểu

    Xét vị trí tương đối

    Xét vị trí tương đối giữa hai đường thẳng d_1:-2x+y+1=0 và d_2:4x - 2y - 2 = 0.

     Ta có: \frac{{ - 2}}{4} = \frac{1}{{ - 2}} = \frac{1}{{ - 2}} nên hai đường thẳng trùng nhau.

  • Câu 37: Thông hiểu

    Tìm các giá trị nguyên của tham số m

    Cho phương trình x^{2} - mx - m^{2} = 0 với m là tham số. Có bao nhiêu giá trị nguyên của tham số m \in \lbrack - 10;10brack để phương trình đã cho có hai nghiệm trái dấu?

    Từ yêu cầu bài toán

    \Leftrightarrow a.c < 0 \Leftrightarrow - m^{2} < 0 \Leftrightarrow m^{2} > 0 \Leftrightarrow m eq 0

    Suy ra m \in \left\{ - 10;....; - 1 ight\} \cup \left\{ 1;...;10 ight\}

    Vậy có 20 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.

  • Câu 38: Thông hiểu

    Tìm tọa độ điểm A

    Cho  có C(–1; 2), đường cao BH: x – y + 2 = 0, đường phân giác trong AN: 2x – y + 5 = 0. Tọa độ điểm A là:

    Ta có: BH \bot AC \Rightarrow \left( {AC} ight):x + y + c = 0

    Mà C\left( { - 1;2} ight) \in \left( {AC} ight)

    \begin{matrix} \Rightarrow - 1 + 2 + c = 0 \hfill \\ \Rightarrow c = - 1 \hfill \\ \end{matrix}

    Vậy (AC):x+y−1=0

    Có A=AN∩AC => A là nghiệm của hệ phương trình

    \left\{ {\begin{array}{*{20}{l}} {x + y - 1 = 0} \\ {2x - y + 5 = 0} \end{array}} ight. \Rightarrow \left\{ {\begin{array}{*{20}{l}} {x = \dfrac{{ - 4}}{3}} \\ {y = \dfrac{7}{3}} \end{array}} ight. \Rightarrow A\left( {\dfrac{{ - 4}}{3};\dfrac{7}{3}} ight)

  • Câu 39: Nhận biết

    Chọn kết luận đúng

    Cho đường thẳng d_{1} có vectơ pháp tuyến là \overrightarrow{n_{1}} và đường thẳng d_{2} có vectơ pháp tuyến là \overrightarrow{n_{2}}. Gọi \beta là góc tạo bởi hai đường thẳng d_{1};d_{2}. Kết luận nào sau đây đúng?

    Góc tạo bởi hai đường thẳng đã cho được xác định bởi công thức \cos\beta = \frac{\left| \overrightarrow{n_{1}}.\overrightarrow{n_{2}} ight|}{\left| \overrightarrow{n_{1}} ight|.\left| \overrightarrow{n_{2}} ight|}.

  • Câu 40: Thông hiểu

    Tìm số hạng không chứa x

    Tìm số hạng không chứa x trong khai triển \left( x^{3} - \frac{1}{x} ight)^{12}.

    Công thức số hạng thứ (k + 1) của khai triển \left( x^{3} - \frac{1}{x} ight)^{12}là:

    T_{k} = C_{12}^{k}( - 1)^{k}\left( x^{3} ight)^{12 - k}.\frac{1}{x^{k}} = C_{12}^{k}( - 1)^{k}{x^{3}}^{6 - 4k},0 \leq k \leq 12,k \in \mathbb{N}.

    Số hạng không chứa x ứng với 36 - 4k = 0 \Leftrightarrow k = 9 (thỏa mãn).

    Suy ra T_{7} = C_{12}^{9}( - 1)^{9} = - 220.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 4 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
  • Điểm thưởng: 0
Xem đáp án Làm lại

Đấu trường Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 4

Đang tìm đối thủ...

Đang tải...

Tạo phòng ngay Đấu trường chung
1
16 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 4
Thời gian còn lại 90:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Tìm bài trong mục này