VnDoc.com Lớp 10 Khóa học Lớp 10 Toán 10 - Chân trời sáng tạo

Đóng

Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm

Mua VnDoc PRO chỉ từ 79.000đ

Đóng

Bạn cần đăng nhập tài khoản Thành viên VnDoc để:

- Xem đáp án

- Nhận 1 lần làm bài trắc nghiệm miễn phí!

Đăng nhập

Đề kiểm tra 45 phút Chương 6 Thống kê Chân trời sáng tạo

Mô tả thêm:

Đề kiểm tra 45 phút Toán 10 Chương 6 Thống kê sách Chân trời sáng tạo giúp bạn học tổng hợp lại kiến thức của cả nội dung chương. Cùng nhau luyện tập nha!

Thời gian làm: 45 phút
Số câu hỏi: 40 câu
Số điểm tối đa: 40 điểm
Tài khoản: Đăng nhập

Trước khi làm bài bạn hãy

1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
4 Căn chỉnh thời gian làm từng câu một cách hợp lý

Bắt đầu làm bài

Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé!

Mua ngay Đổi điểm

Đổi điểm làm bài

Điểm khả dụng: 0 điểm

Bạn sẽ dùng 50 điểm để đổi lấy 1 lượt làm bài.

Bạn không đủ điểm để đổi.

Câu 1: Nhận biết
Xác định khoảng biến thiên của mẫu số liệu

Kết quả thống kê số tiền điện của một hộ gia đình trong 6 tháng liên tiếp (đơn vị: nghìn đồng) như sau: $270;\ 300;\ 350;\ 320;\ 310;\ 280$ . Khoảng biến thiên của mẫu số liệu bằng:
- A.
  $70$
- B.
  $90$
- C.
  $40$
- D.
  $80$
Giá trị lớn nhất bằng 350

Giá trị nhỏ nhất bằng 270

=> Khoảng biến thiên của mẫu số liệu là: 350 – 270 = 80.

Vậy khoảng biến thiên của mẫu số liệu bằng 80.
Câu 2: Thông hiểu
Chọn đáp án thích hợp

Viết các số gần đúng sau dưới dạng chuẩn $a = 467346 \pm 12$ .
- A.
  $46735.10$ .
- B.
  $47.10^{4}$ .
- C.
  $467.10^{3}$ .
- D.
  $4673.10^{2}$ .
Ta có $\frac{10}{2} = 5 < 12 < \frac{100}{2} = 50$ nên chữ số hàng trăm trở đi là chữ số chữ số chắc

Do đó số gần đúng viết dưới dạng chuẩn là $4673.10^{2}$ .
Câu 3: Nhận biết
Tính số trung bình cộng

Điểm kiểm tra môn Hóa của một nhóm gồm 9 bạn như sau: 1; 1; 3; 6; 7; 8; 8; 9; 10. Tính trung bình cộng của mẫu số liệu trên. (làm tròn đến hàng phần chục)
- A.
  $5,9$
- B.
  $5,8$
- C.
  $6,2$
- D.
  $6,3$
Số trung bình của mẫu số liệu trên là: $\overline{x} = \frac{1 + 1 + 3 + 6 + 7 + 8 + 8 + 9 + 10}{9} \approx 5,9$ .
Câu 4: Nhận biết
Tìm số quy tròn của số gần đúng

Cho số $a = 367\ 653\ 964\ \pm 213.$ Số quy tròn của số gần đúng $367\ 653\ 964$ là:
- A.
  $367\ 653\ 960$ .
- B.
  $367\ 653\ 000$ .
- C.
  $367\ 654\ 000$ .
- D.
  $367\ 653\ 970$ .
Vì độ chính xác đến hàng trăm nên ta quy tròn đến hàng nghìn và theo quy tắc làm tròn nên số quy tròn là: $367\ 654\ 000$ .
Câu 5: Thông hiểu
Chọn đáp án đúng

Xác định các tứ phân vị của mẫu số liệu: $60;78;80;64;70;76;80;74;86;90$ ?
- A.
  $Q_{1} = 72,Q_{2} = 78,Q_{3} = 80$
- B.
  $Q_{1} = 70,Q_{2} = 75,Q_{3} = 80$
- C.
  $Q_{1} = 70,Q_{2} = 76,Q_{3} = 80$
- D.
  $Q_{1} = 70,Q_{2} = 77,Q_{3} = 80$
Sắp xếp mẫu dữ liệu theo thứ tự không giảm như sau:

$60;64;70;74;76;78;80;80;86;90$

Ta có: $N = 10$ suy ra trung vị bằng trung bình cộng của dữ liệu nằm ở vị trí thứ 5 và thứ 6

$Q_{2} = \frac{76 + 78}{2} = 77$

Vậy đáp án đúng là: $Q_{1} = 70,Q_{2} = 77,Q_{3} = 80$ .
Câu 6: Thông hiểu
Chọn đáp án đúng

Cho giá trị gần đúng của $\frac{8}{17}$ là $0,47$ . Sai số tuyệt đối của số $0,47$ là
- A.
  $0,001$ .
- B.
  $0,003$ .
- C.
  $0,002$ .
- D.
  $0,004$ .
Ta có $\Delta_{a} = \left| \frac{8}{17} - 0,47 \right| = 0,00058 < 0,001$ .
Câu 7: Nhận biết
Tính số trung bình cộng của mẫu số liệu

Để điều tra các con trong mỗi gia đình của một chung cư gồm 100 gia đình. Người ta chọn ra 20 gia đình ở tầng 4 và thu được mẫu số liệu sau đây:
2 4 2 1 3 5 1 1 2 3 1 2 2 3 4 1 1 2 3 4.
Số trung bình cộng $\bar{x}$ của mẫu số liệu trên là:
- A.
  2,34
- B.
  2,3
- C.
  2,4
- D.
  2,35
Số trung bình cộng của mẫu số liệu trên là:
$\overline x = \frac{{1.6 + 2.6 + 3.4 + 4.3 + 5}}{{20}} = 2,35$
Câu 8: Thông hiểu
Xác định sai số tuyệt đối

Hãy xác định sai số tuyệt đối của số $a = 123456$ biết sai số tương đối $\delta_{a} = 0,2\%$
- A.
  146,912.
- B.
  617280.
- C.
  24691,2.
- D.
  61728000
Ta có $\delta_{a} = \frac{\Delta_{a}}{|a|} \Rightarrow \Delta_{a} = \delta_{a}|a| = 146,912$ .
Câu 9: Nhận biết
Tính độ lệch chuẩn

Tính độ lệch chuẩn của mẫu số liệu: 10; 8; 6; 2; 4.
- A.
  $2\sqrt{3}$
- B.
  $2\sqrt{2}$
- C.
  $\sqrt{2}$
- D.
  $4\sqrt{2}$
Số trung bình là $\overline{x} =$ $\frac{10 + 8 + 6 + 2 + 4}{5}$ $= 6$ .

Phương sai là $s^{2} =$ $\frac{(10 - 6)^{2} + (8 - 6)^{2} + (6 - 6)^{2} + (2 - 6)^{2} + (4 - 6)^{2}}{5}$ $= 8$ .

Độ lệch chuẩn là $\sqrt{s^{2}} = \sqrt{8} = 2\sqrt{2}$ .
Câu 10: Thông hiểu
Viết giá trị gần đúng của số đã cho

Sử dụng máy tính bỏ túi, hãy viết giá trị gần đúng của $\sqrt{3}$ chính xác đến hàng phần nghìn.
- A.
  1,7320.
- B.
  1,732.
- C.
  1,733.
- D.
  1,731.
Ta có:

$\sqrt{3}\overset{MTCT}{\rightarrow}\sqrt{3} = 1,7320508076...\overset{}{\rightarrow}$ Làm tròn đến hàng phần nghìn ta được kết quả: $1,732$ .
Câu 11: Thông hiểu
Tính khối lượng trung bình của ba nhóm học sinh

Ba nhóm học sinh gồm 5 người, 10 người và 15 người. Khối lượng trung bình của mỗi nhóm lần lượt là 48 kg, 45kg và 40 kg. Khối lượng trung bình của 3 nhóm học sinh là:
- A.
  42kg
- B.
  64,5kg
- C.
  44,3kg
- D.
  43kg
Khối lượng trung bình của 3 nhóm học sinh là:
$\overline x = \frac{{48.5 + 45.10 + 40.15}}{{5 + 10 + 15}} = 43$
Câu 12: Nhận biết
Chọn đáp án đúng

Cho $a$ là số gần đúng của số đúng $\overline{a}$ . Khi đó $\Delta_{a} = \left| \overline{a} - a ight|$ gọi là:
- A.
  Số quy tròn của $\overline{a}$
- B.
  Sai số tương đối của số gần đúng $a$ .
- C.
  Số quy tròn của $a$
- D.
  Sai số tuyệt đối của số gần đúng $a$ .
Ta có: $\Delta_{a} = \left| \overline{a} - a ight|$ gọi là sai số tuyệt đối của số gần đúng $a$ .
Câu 13: Thông hiểu
Tính độ lệch chuẩn của mẫu số liệu

Cho mẫu số liệu: $10;8;6;2;4$ . Tính độ lệch chuẩn của mẫu số liệu đó?
- A.
  $4$
- B.
  $2\sqrt{2}$
- C.
  $6$
- D.
  $8$
Ta có: $N = 5$

Số trung bình của mẫu số liệu là:

$\overline{x} = \frac{10 + 8 + 6 + 2 + 4}{5} = 6$

Phương sai của mẫu số liệu là:

$s^{2} = \frac{(10 - 6)^{2} + (8 - 6)^{2} + (6 - 6)^{2} + (2 - 6)^{2} + (4 - 6)^{2}}{5} = 8$

Suy ra độ lệch chuẩn của mẫu số liệu là:

$s = \sqrt{s^{2}} = 2\sqrt{2}$

Vậy độ lệch chuẩn bằng $2\sqrt{2}$ .
Câu 14: Nhận biết
Chọn công thức đúng

Khoảng biến thiên tứ phân vị $\Delta Q$ được xác định bởi:
- A.
  $Q_{3} - Q_{1}$
- B.
  $Q_{3} - Q_{2}$
- C.
  $Q_{2} - Q_{1}$
- D.
  $Q_{2} + Q_{1}$
Khoảng biến thiên tứ phân vị $\Delta Q$ được xác định bởi $Q_{3} - Q_{1}$ .
Câu 15: Thông hiểu
Chọn phát biểu đúng

Tìm phát biểu đúng về phương sai của một mẫu số liệu.
- A.
  Phương sai được sử dụng làm đại diện cho các số liệu của mẫu.
- B.
  Phương sai được sử dụng để đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình).
- C.
  Phương sai được tính bằng tổng số phần tử của một mẫu số liệu.
- D.
  Phương sai là số liệu xuất hiện nhiều nhất (số liệu có tần số lớn nhất) trong bảng các số liệu thống kê.
Ý nghĩa của phương sai: Phương sai được sử dụng để đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình).
Câu 16: Nhận biết
Xác đinh mốt của bảng số liệu

Một shop bán giày thống kê số lượng giày bán trong vài ngày trong bảng sau:

Cỡ giày

37

38

39

40

41

42

Số lượng

35

42

50

38

32

48

Mốt của bảng số liệu trên là:
- A.
  $42$
- B.
  $39$
- C.
  $50$
- D.
  $41$
Mốt là giá trị có tần số lớn nhất trong bảng số liệu

Quan sát bảng số liệu đã cho suy ra mốt của bảng số liệu là 39.
Câu 17: Vận dụng
Tìm tứ phân vị trên

Tìm tứ phân vị trên của bảng số liệu sau:
- A.
  28
- B.
  27
- C.
  26
- D.
  29
Cỡ mẫu số liệu trên là: $n = 10 + 8 + 4 + 2 + 1 = 25$ .

Giá trị chính giữa của mẫu là giá trị ở vị trí thứ 13, đó là số 27. Suy ra $M_{e} = Q_{2} = 27$ .

Ta đi tìm trung vị của mẫu số liệu gồm 12 giá trị bên phải $M_{e}$ . Hai giá trị chính giữa là giá trị ở vị trí thứ 19 và 20. Đó là số 28 và số 28.

Suy ra $Q_{3} = \frac{28 + 28}{2} = 28$ . Vậy tứ phân vị trên là 28.
Câu 18: Nhận biết
Tìm mốt của mẫu số liệu số liệu không ghép nhóm

Điều tra tiền lương một tháng của 100 người lao động trên địa bàn một xã ta có bàng phân bố tần số sau:

Tiền lương (VND)

5.000.000

6.000.000

7.000.000

8.000.000

9.000.000

9.500.000

Tần số

26

34

20

10

5

5

Tìm mốt của bảng phân bổ tần số trên.
- A.
  5.000.000.
- B.
  6.000.000.
- C.
  7.500.000.
- D.
  9.500.000.
Ta có giá trị 6.000.000 có tần số lớn nhất nên là mốt của bảng phân bố tần số trên.
Câu 19: Nhận biết
Tính sai số tuyệt đối

Đo chiều dài của một cây thước, ta được kết quả $\overline{a} = 45 \pm 0,3\ (cm)$ . Khi đó sai số tuyệt đối của phép đo được ước lượng là
- A.
  $\Delta_{45} = 0,3$ .
- B.
  $\Delta_{45} \leq 0,3$ .
- C.
  $\Delta_{45} \leq - 0,3$ .
- D.
  $\Delta_{45} = - 0,3$ .
Ta có độ dài dài gần đúng của cây thước là $a = 45$ với độ chính xác $d = 0,3$

Nên sai số tuyệt đối $\Delta_{45} \leq d = 0,3$
Câu 20: Nhận biết
Tìm khoảng tứ phân vị

Tìm khoảng tứ phân vị mẫu số liệu điểm của một nhóm học sinh lớp 10:
- A.
  $3$
- B.
  $4$
- C.
  $3,5$
- D.
  $2$
Sắp xếp mẫu số liệu theo thứ tự không giảm: 4 5 5 6 7 7 7 8 8 9 9 10.

Hai số liệu chính giữa là 7 và 7 nên $Q_{2} = \frac{7 + 7}{2} = 7$ .

Trung vị của mẫu số liệu 4 5 5 6 7 7 chính là $Q_{1} = \frac{5 + 6}{2} = 5,5$ .

Trung vị của mẫu số liệu 7 8 8 9 9 10 chính là $Q_{3} = \frac{8 + 9}{2} = 8,5$ .

Khoảng tứ phân vị $\Delta_{Q} = Q_{3} - Q_{1} =$ $8,5 - 5,5 = 3$ .
Câu 21: Thông hiểu
Tính số trung bình cộng

Kết quả điểm kiểm tra 45 phút môn Hóa Học của 100 em học sinh được trình bày ở bảng sau:

Điểm

3

4

5

6

7

8

9

10

Cộng

Tần số

3

5

14

14

30

22

7

5

100

Số trung bình cộng của bảng phân bố tần số nói trên là:
- A.
  6,82.
- B.
  4.
- C.
  6,5.
- D.
  7,22.
Số trung bình cộng của bảng phân bố tần số nói trên là

$\bar{x} = \frac{3.3 + 4.5 + 5.14 + 6.14 + 7.30 + 8.22 + 9.7 + 10.5}{100} = 6,82.$
Câu 22: Vận dụng
Tìm trung vị

Bảng dưới đây thống kê điểm Văn của lớp 11C.

Biết $n\mathbb{\in N}$ . Tìm trung vị của bảng số liệu.
- A.
  6
- B.
  5
- C.
  8
- D.
  7
Vì tổng số học sinh bằng 40 nên ta có: $5n + 15 = 40 \Leftrightarrow n = 5$ .

Thống kê lại bảng:

Hai giá trị chính giữa của mẫu số liệu là giá trị ở vị trí thứ 20 và 21. Đó là số 6 và số 6.

Suy ra trung vị $M_{e} = \frac{6 + 6}{2} = 6$ .
Câu 23: Thông hiểu
Tìm giá trị bất thường

Tìm các giá trị bất thường của mẫu số liệu:

5 6 19 21 22 23 24 25 26 27 28 29 30 31 32 33 34 48 49
- A.
  5; 6; 48; 49
- B.
  5 và 49
- C.
  5
- D.
  49
Mẫu số liệu đã được sắp xếp theo thứ tự không giảm.

Giá trị chính giữa là 27 nên $Q_{2} = 27$ .

Giá trị chính giữa của mẫu 5 6 19 21 22 23 24 25 26 là 22 nên $Q_{1} = 22$ .

Giá trị chính giữa của mẫu 28 29 30 31 32 33 34 48 49 là 32 nên $Q_{3} = 32$ .

Khoảng tứ phân vị $\Delta_{Q} = 32 - 22 = 10$ .

Ta có: $Q_{1} - 1,5\Delta_{Q} =$ $22 - 1,5.10 = 7$ .

Ta co: $Q_{3} - 1,5\Delta_{Q} =$ $32 + 1,5.10 = 47$ .

Ta thấy có giá trị 5 và 6 nhỏ hơn 7 nên đây là 2 giá trị bất thường.

Ta thấy có 48 và 49 là hai giá trị lớn hơn 47 nên đây là 2 giá trị bất thường.
Câu 24: Nhận biết
Chọn đáp án đúng

Số quy tròn của số gần đúng $a$ với $\overline{a} = 18658 \pm 25$ là:
- A.
  $19000$
- B.
  $18800$
- C.
  $18600$
- D.
  $18700$
Quy tròn $a$ đến hàng trăm nên số quy tròn của số gần đúng $a$ là: $18700$ .
Câu 25: Thông hiểu
Tính thời gian chạy trung bình

Cho bảng số liệu thống kê kết quả thi chạy 100m của một nhóm học sinh (đơn vị: giây) như sau:

Thời gian

12

13

14

15

16

Số học sinh

6

4

5

3

2

Tính thời gian chạy trung bình của nhóm học sinh đó?
- A.
  $12,75$
- B.
  $12,85$
- C.
  $13,55$
- D.
  $13,44$
Số học sinh tham gia chạy là 20 (học sinh)

Thi gian chạy trung bình của nhóm 20 học sinh là:

$\overline{x} = \frac{6.12 + 4.13 + 5.14 + 3.15 + 2.16}{20} = 13,55$ (giây)

Vậy thời gian chạy trung bình của nhóm học sinh bằng 13,55 giây.
Câu 26: Thông hiểu
Tính sai số tương đối

Bạn Linh đo quãng đường đi học từ nhà đến trường là $a = 568m$ với độ chính xác $d = 0,3m$ . Sai số tương đối trong phép đo là:
- A.
  $0,05\%$
- B.
  $0,5\%$
- C.
  $0,03\%$
- D.
  $0,005\%$
Sai số tương đối trong phép đo là $\delta = \frac{d}{|a|} = \frac{0,3}{568} \approx 0,05\%$ .
Câu 27: Nhận biết
Tìm khoảng biến thiên

Điều tra về số học sinh của một trường THPT như sau:
Khối lớp
10
11
12
Số học sinh
1120
1075
900
Khoảng biến thiên của mẫu số liệu trên là.
- A.
  220
- B.
  45
- C.
  175
- D.
  3095
Khoảng biến thiên R = 1120 - 900 = 220.
Câu 28: Nhận biết
Tìm khoảng tứ phân vị

Chiều cao của một số học sinh nữ lớp 9 (đơn vị cm) được cho trong bảng.

Tìm khoảng tứ phân vị của mẫu số liệu này.
- A.
  11
- B.
  12
- C.
  16
- D.
  15
Nhận thấy mẫu đã được sắp xếp theo thứ tự không giảm.

Số liệu chính giữa là 162 nên $Q_{2} = 162$ .

Số liệu chính giữa của mẫu 151 152 153 154 155 160 160 là 154 nên $Q_{1} = 154$ .

Số liệu chính giữa của mẫu 163 165 165 165 166 167 167 là 165 nên $Q_{3} = 165$ .

Khoảng tứ phân vị $\Delta_{Q} = Q_{3} - Q_{1} =$ $165 - 154 = 11$ .
Câu 29: Nhận biết
Chọn khẳng định đúng

Khẳng định nào sau đây là đúng?
- A.
  Nếu sai số tương đối của phép đo càng lớn thì chất lượng phép đo càng cao.
- B.
  Nếu sai số tương đối của phép đo càng nhỏ thì chất lượng phép đo càng thấp.
- C.
  Nếu sai số tương đối của phép đo càng nhỏ thì chất lượng phép đo càng cao.
- D.
  Không thể biết được chất lượng phép đo thông qua sai số tương đối.
Khẳng định đúng là: "Nếu sai số tương đối của phép đo càng nhỏ thì chất lượng phép đo càng cao."
Câu 30: Nhận biết
Tìm khoảng biến thiên R

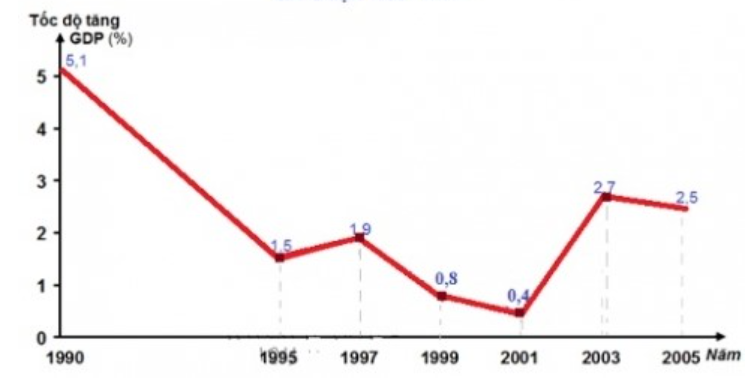
Cho một mẫu dữ liệu đã được sắp xếp theo thứ tự không giảm $x_1 ≤ x_2 ≤ x_3 ≤ ... ≤ x_n$ . Khi đó khoảng biến thiên $R$ của mẫu số liệu bằng:
- A.
  $R = x_n – x_1$
- B.
  $R = x_1 - x_n$
- C.
  $R=\frac{x_n-x_1}{2}$
- D.
  $R=\frac{x_1-x_n}{2}$
Khoảng biến thiên của mẫu số liệu bằng: $R = x_n – x_1$
Câu 31: Thông hiểu
Chọn đáp án đúng

Xác định khoảng tứ phân vị của mẫu số liệu: $2;3;4;5;6$ ?
- A.
  $\Delta Q = 3$
- B.
  $\Delta Q = 1$
- C.
  $\Delta Q = - 2$
- D.
  $\Delta Q = - 1$
Ta có: $N = 5$ là số lẻ

Suy ra $Q_{2} = 4$

$\Rightarrow \left\{ \begin{matrix}Q_{1} = \dfrac{2 + 3}{2} = 2,5 \\Q_{3} = \dfrac{5 + 6}{2} = 5,5 \\\end{matrix} ight.\ \Rightarrow \Delta Q = 5,5 - 2,5 = 3$

Vậy khoảng tứ phân vị của mẫu số liệu bằng 3.

Câu 32: Vận dụng

Tính độ lệch chuẩn

Nhiệt độ (đơn vị: ⁰C) tại Mộc Châu trong một ngày sau một vài lần đo như sau:

$21^{0}C;23^{0}C;25^{0}C;28^{0}C;30^{0}C;$

$32^{0}C;34^{0}C;31^{0}C;29^{0}C;26^{0}C.$

Kết quả nào dưới đây gần nhất với độ lệch chuẩn của mẫu số liệu đã cho?

A.
$3,91$
B.
$4$
C.
$3,8$
D.
$3,9$

Ta có: $N = 10$

Nhiệt độ trung bình trong ngày là:

$\overline{x} = \frac{21 + 23 + 25 + 28 + 30 + 32 + 34 + 31 + 29 + 26}{10} = 27,9$

Ta có bảng sau:

Giá trị	Độ lệch	Bình phương độ lệch
21	$21 - 27,9 = - 6,9$	47,61
23	$23 - 27,9 = - 4,9$	24,01
25	$25 - 27,9 = - 2,9$	8,41
28	$28 - 27,9 = 0,1$	0,01
30	$30 - 27,9 = 2,1$	4,41
32	$32 - 27,9 = 4,1$	16,81
34	$34 - 27,9 = 6,1$	37,21
31	$31 - 27,9 = 3,1$	9,61
29	$29 - 27,9 = 1,1$	1,21
26	$26 - 27,9 = - 1,9$	3,61
Tổng		152,9

Suy ra phương sai của mẫu số liệu là: $s^{2} = \frac{152,9}{10} = 15,29$

Suy ra độ lệch chuẩn của mẫu số liệu là: $s = \sqrt{s^{2}} \approx 3,91$

Câu 33: Nhận biết
Tìm mốt của bảng số liệu

Cho bảng số liệu số máy tính bán được trong quý I đầu năm 2022 của một cửa hàng:

Hãng

HP

Lenovo

Asus

Apple

Dell

Razer

Số máy tính bán được

55

45

42

36

60

15

Mốt của bảng số liệu trên là hãng máy tính nào?
- A.
  Dell
- B.
  HP
- C.
  Apple
- D.
  Lenovo
Số máy tính bán được nhiều nhất là 60 máy thuộc hãng Dell

=> Mốt của bảng số liệu trên là hãng Dell.
Câu 34: Thông hiểu
Tìm độ lệch chuẩn

Tìm độ lệch chuẩn của dãy số liệu: 18 14 15 8.
- A.
  $13,75$
- B.
  $14$
- C.
  $\frac{\sqrt{55}}{2}$
- D.
  $\frac{55}{2}$
Số trung bình của mẫu số liệu là: $\overline{x}$ $= \frac{8 + 15 + 14 + 18}{4}$ $= 13$ .

Ta có phương sai: $s^{2} =$ $\frac{(8 - 13)^{2} + (15 - 13)^{2} + (14 - 13)^{2} + (18 - 13)^{2}}{4}$ $= 13,75$ .

Độ lệch chuẩn: $\sqrt{s^{2}} = \sqrt{13,75} = \frac{\sqrt{55}}{2}$ .
Câu 35: Vận dụng
Chọn kết luận đúng

Một người cần đo chiều cao của một cái cây. Anh ta thực hiện ba phép đo, kết quả được ghi lại như sau: $h_{1} = 10,23 \pm 0,43$ (m), $h_{2} = 10,58 \pm 0,2$ (m), $h_{3} = 9,92 \pm 0,63$ (m). Trong ba số liệu trên, người thợ nên chọn số liệu nào làm chiều cao của cái cây?
- A.
  Chọn $h_{1}$ .
- B.
  Chọn $h_{2}$ .
- C.
  Chọn $h_{3}$ .
- D.
  Chọn $h_{1}$ hoặc $h_{2}$ .
Phép đo lần 1 có sai số tương đối $\delta_{1} \leq \frac{0,43}{10,23} \approx 0,042 = 4,2\%$ .

Phép đo lần 2 có sai số tương đối $\delta_{2} \leq \frac{0,2}{10,58} \approx 0,0189 = 1,89\%$ .

Phép đo lần 3 có sai số tương đối $\delta_{3} \leq \frac{0,63}{9,92} \approx 0,0635 = 6,35\%$ .

Vì phép đo lần 2 có sai số nhỏ nhất nên người thợ nên chọn $h_{2}$ làm chiều cao của ngôi nhà.
Câu 36: Nhận biết
Hãy viết chuẩn số gần đúng của a

Cho số $a = 1754731$ , trong đó chỉ có chữ số hàng trăm trở lên là đáng tin. Hãy viết chuẩn số gần đúng của $a$ .
- A.
  $17547.10^{2}$ .
- B.
  $17548.10^{2}$ .
- C.
  $1754.10^{3}$ .
- D.
  $1755.10^{2}$ .
Chuẩn số gần đúng của số a là $17547.10^{2}$
Câu 37: Nhận biết
Viết số quy tròn

Hãy viết số quy tròn của số gần đúng sau: $4,1356 ± 0,001$
- A.
  4,12
- B.
  4,13
- C.
  4,14
- D.
  4,15
Ta có:hàng lớn nhất có độ chinh xác d = 0,001 là hàng phần nghìn
=> Ta quy tròn số đến hàng phần trăm
Vậy số quy tròn là 4,14.
Câu 38: Nhận biết
Xác định mốt của mẫu số liệu

Cho bảng kết quả kiểm tra khối lượng của 30 quả trứng gà như sau:

Khối lượng (gram)

25

30

35

40

45

50

Số quả trứng

3

5

7

9

4

2

Xác định mốt của mẫu số liệu?
- A.
  $35$
- B.
  $40$
- C.
  $50$
- D.
  $9$
Mốt của mẫu số liệu là 40 (vì có tần số lớn nhất).
Câu 39: Vận dụng
Chọn đáp án đúng

Một cái ruộng hình chữ nhật có chiều dài là $x = 23m \pm 0,01m$ và chiều rộng là $y = 15m \pm 0,01m$ . Chu vi của ruộng là:
- A.
  $P = 76m \pm 0,4m$
- B.
  $P = 76m \pm 0,04m$
- C.
  $P = 76m \pm 0,02m$
- D.
  $P = 76m \pm 0,08m$
Giả sử $x = 23 + a,\ \ y = 15 + b$ với $- 0,01 \leq a,\ \ b \leq 0,01$ .

Ta có chu vi ruộng là:

$P = 2(x + y) = 2(38 + a + b) = 76 + 2(a + b)$ .

Vì $- 0,01 \leq a,\ \ b \leq 0,01$ nên $- 0,04 \leq 2(a + b) \leq 0,04$ .

Do đó $|P - 76| = \left| 2(a + b) \right| \leq 0,04$ .

Vậy $P = 76m \pm 0,04m$ .
Câu 40: Vận dụng
Tìm giá trị bất thường

Hình dưới thống kê tỉ lệ phần trăm thất nghiệp ở một số quốc gia:

Hãy tìm giá trị bất thường (nếu có) của mẫu số liệu.
- A.
  12,75
- B.
  8,6
- C.
  3,2
- D.
  Không có
Sắp xếp các giá trị theo thứ tự không giảm:

3,2 3,6 4,4 4,5 5,0 5,4 6,0 6,7 7,0 7,2 7,7 7,8 8,4 8,6 8,7

Từ mẫu số liệu ta tính được: $Q_{2} = 6,7$ và $Q_{1} = 4,5$ , $Q_{3} = 7,8$ .

Suy ra $\Delta_{Q} = Q_{3} - Q_{1} = 7,8 - 4,5 = 3,3$ .

Ta có: $Q_{1} - 1,5\Delta_{Q} = 4,5 - 1,5.3,3$ $= - 0,45$ .

Ta có: $Q_{3} + 1,5\Delta_{Q} = 7,8 + 1,5.3,3$ $= 12,75$ .

Ta thấy không có số liệu nào nhỏ hơn $- 0,45$ và lớn hơn $12,75$ nên mẫu không có giá trị bất thường.

Mua ngay Đổi điểm

Đổi điểm làm bài

Điểm khả dụng: 0 điểm

Bạn sẽ dùng 50 điểm để đổi lấy 1 lượt làm bài.

Bạn không đủ điểm để đổi.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 6 Thống kê Chân trời sáng tạo Kết quả

Thời gian làm bài: 00:00:00
Số câu đã làm: 0
Điểm tạm tính: 0
Điểm thưởng: 0
Tài khoản làm: Đăng nhập

Làm lại

Tải file làm trên giấy

Chia sẻ bởi:
Khang Anh

25 Bài viết đã được lưu

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Số điện thoại này đã được xác thực!

Bạn có thể dùng Sđt này đăng nhập tại đây!

Lỗi gửi SMS, liên hệ Admin

Sắp xếp theo

Xóa Đăng nhập để Gửi

Đề kiểm tra 45 phút Chương 6 Thống kê Chân trời sáng tạo

Thời gian còn lại 45:00 Số câu đã làm 0/40

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

Chưa làm Đã làm

Làm lại Nộp bài

Tìm bài trong mục này

Chương 1: Mệnh đề và tập hợp
Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
Chương 3: Hàm số bậc hai và đồ thị
Chương 4: Hệ thức lượng trong tam giác
Chương 5: Vectơ
Đề kiểm tra học kì 1
Chương 6: Thống kê
Chương 7: Bất phương trình bậc hai một ẩn
Chương 8: Đại số tổ hợp
Đề thi giữa học kì 2
Chương 9: Phương pháp tọa độ trong mặt phẳng
Chương 10: Xác suất
Đề thi học kì 2

Tiền lương (VND)	5.000.000	6.000.000	7.000.000	8.000.000	9.000.000	9.500.000
Tần số	26	34	20	10	5	5

Hãng	HP	Lenovo	Asus	Apple	Dell	Razer
Số máy tính bán được	55	45	42	36	60	15

Khối lượng (gram)	25	30	35	40	45	50
Số quả trứng	3	5	7	9	4	2

Cỡ giày	37	38	39	40	41	42
Số lượng	35	42	50	38	32	48

Điểm	3	4	5	6	7	8	9	10	Cộng
Tần số	3	5	14	14	30	22	7	5	100

Thời gian	12	13	14	15	16
Số học sinh	6	4	5	3	2

Khối lớp	10	11	12
Số học sinh	1120	1075	900

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Đấu Trường Tri Thức

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Đề kiểm tra 45 phút Chương 6 Thống kê Chân trời sáng tạo

Đổi điểm làm bài

Đổi điểm làm bài

Chúc mừng Bạn đã hoàn thành bài!