Nhị thức Newton sách CTST
Ta có hai công thức khai triển sau:
\(\begin{array}{l}
\begin{array}{*{20}{l}}
{{{\left( {a + b} \right)}^4} = {C_4}^0{a^4} + {C_4}^1{a^3}b + {C_4}^2{a^2}{b^2} + {C_4}^3a{b^3} + {C_4}^4{b^4}}\\
{\;\;\;\;\;\;\;\;\;\;\;\;\; = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}.}
\end{array}\\
\begin{array}{*{20}{l}}
{{{\left( {a + b} \right)}^5} = {C_4}^0{a^5} + {C_5}^1{a^4}b + {C_5}^2{a^3}{b^2} + {C_5}^3{a^2}{b^3} + {C_5}^4a{b^4} + {C_5}^5{b^5}}\\
{\;\;\;\;\;\;\;\;\;\;\;\;\; = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}.}
\end{array}
\end{array}\)
Hai công thức trên gọi là công thức nhị thức Newton (gọi tắt là nhị thức Newton) \({\left( {a + b} \right)^n}\) ứng với n = 4 và n = 5.
Chú ý
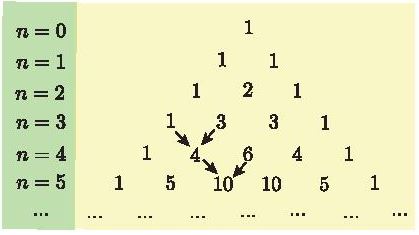
Các hệ số trong khai triển nhị thức Newton \({\left( {a + b} \right)^n}\) với \(n = 0; 1; 2; 3;...\) được viết thành từng hàng và xếp thành bảng số như bên. Bảng số này có quy luật: số đầu tiên và số cuối cùng của mỗi hàng đều là 1; tổng của hai số liên tiếp cùng hàng bằng số của hàng kế dưới ở vị trí giữa hai số đó (được chỉ bởi mũi tên trên bảng).
Bảng số trên được gọi là tam giác Pascal (đặt theo tên của nhà toán học, vật lí học, triết học người Pháp Blaise Pascal, 1623 — 1662).
Ví dụ: Sử đụng công thức nhị thức Newton, hãy khai triển
| a) \({{{\left( {x + 3} \right)}^4}}\) |
b) \({{{\left( {1 - x} \right)}^5}}\) |
Hướng dẫn giải
a) Theo công thức nhị thức Newton, ta có
\(\begin{array}{*{20}{l}}
{{{\left( {x + 3} \right)}^4} = 1.{x^4} + 4.{x^3}.3 + 6.{x^2}{{.3}^2} + 4.x{{.3}^3} + {{1.3}^4}} \\
{ = {x^4} + 4.3.{x^3} + 6.9.{x^2} + 4.27.x + 81} \\
{ = {x^4} + 12.{x^3} + 54{x^2} + 108.x + 81}
\end{array}\)
b) Theo công thức nhị thức Newton, ta có:
\(\begin{array}{*{20}{l}}
{{{\left( {1 - x} \right)}^5} = 1 + 5.\left( { - x} \right) + 10.{{\left( { - x} \right)}^2} + 10.{{\left( { - x} \right)}^3} + 5.{{\left( { - x} \right)}^4} + 1{{\left( { - x} \right)}^5}} \\
{ = 1 - 5x + 10{x^2} - 10{x^3} + 5{x^4} - {x^5}}
\end{array}\)
