Tìm điểm thuộc đồ thị
Điểm nào sau đây thuộc đồ thị của hàm số ![]() ?
?
Thử trực tiếp thấy tọa độ của M(2;0) thỏa mãn phương trình hàm số.
Đề kiểm tra 45 phút Toán 10 Chương 3 Hàm số bậc hai và đồ thị sách Chân trời sáng tạo giúp bạn học tổng hợp lại kiến thức của cả nội dung chương. Cùng nhau luyện tập nha!
Tìm điểm thuộc đồ thị
Điểm nào sau đây thuộc đồ thị của hàm số ![]() ?
?
Thử trực tiếp thấy tọa độ của M(2;0) thỏa mãn phương trình hàm số.
Hàm số nghịch biến
Trong các hàm số sau, hàm số nào là nghịch biến:
Ta có:
Hàm số có a = -2 < 0
=> Hàm số nghịch biến.
Chọn khẳng định đúng
Hàm số y = x2 − 4x + 3 đồng biến trên khoảng nào?
Trục đối xứng x = 2. Ta có a = 1 > 0 nên hàm số nghịch biến trên khoảng (−∞; 2) và đồng biến trên khoảng (2; +∞).
Tìm hàm số bậc hai thỏa mãn
Xác định parabol ![]() biết rằng Parabol đi qua hai điểm M(1;5) và N(-2;8)
biết rằng Parabol đi qua hai điểm M(1;5) và N(-2;8)
Thay tọa độ và
vào
. Ta có:
.
Do đó .
Tìm hệ số góc
Hệ số góc của đồ thị hàm số y = 2018x − 2019 bằng
Hệ số góc a = 2018.
Chọn khẳng định đúng
Cho hàm số có đồ thị như hình bên dưới.
Khẳng định nào sau đây là đúng?
Trên khoảng (0;2) đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
Tìm tập xác định
Tìm tập xác định của ![]()
Điều kiện xác định: .
Vậy .
Tìm công thức hàm số bậc hai
Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?
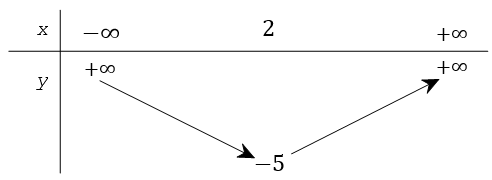
Nhận xét:
Bảng biến thiên có bề lõm hướng lên. Loại đáp án y = − x2 + 4x − 9 và y = − x2 + 4x.
Đỉnh của parabol có tọa độ là (2;−5). Xét các đáp án, đáp án y = x2 − 4x − 1 thỏa mãn.
Chọn khẳng định sai
Cho hàm số y = f(x) có tập xác định là [ − 1; 3] và đồ thị của nó được biểu diễn bởi hình bên.
Khẳng định nào sau đây là sai?
Trên khoảng (0;2) đồ thị hàm số đi ngang từ trái sang phải
Hàm số không đổi trên khoảng (0;2).
Trên khoảng (2;3) đồ thị hàm số đi lên từ trái sang phải
Hàm số đồng biến trên khoảng (2;3).
Chọn đáp án Hàm số đồng biến trên khoảng (2;3).
Tìm công thức của Parabol
Tìm parabol (P) : y = ax2 + 3x − 2, biết rằng parabol có trục đối xứng x = − 3.
Vì (P) có trục đối xứng x = − 3 nên .
Vậy .
Tìm tập xác định của hàm số
Tập xác định của hàm số ![]() là:
là:
Hàm số xác định ⇔ x − 1 ≥ 0 ⇔ x ≥ 1.
Tính chiều cao h của Parabol
Một chiếc cổng hình parabol có phương trình ![]() . Biết cổng có chiều rộng d = 5 mét (như hình vẽ). Hãy tính chiều cao h của cổng.
. Biết cổng có chiều rộng d = 5 mét (như hình vẽ). Hãy tính chiều cao h của cổng.
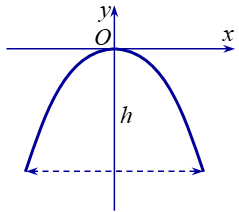
Gọi Avà Blà hai điểm ứng với hai chân cổng như hình vẽ.
Vì cổng hình parabol có phương trình và cổng có chiều rộng d = 5 mét nên:
AB = 5 và .
Vậy chiều cao của cổng làmét.
Tìm m thỏa mãn điều kiện
Cho hàm số ![]() xác định trên [ − 1; 1]. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [ − 1; 1] lần lượt là y1, y2 thỏa mãn y1 − y2 = 8. Khi đó giá trị của m bằng
xác định trên [ − 1; 1]. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [ − 1; 1] lần lượt là y1, y2 thỏa mãn y1 − y2 = 8. Khi đó giá trị của m bằng
Đặt .
Hoành độ đỉnh của đồ thị hàm số là .
Vì hệ số a = 1 > 0 nên hàm số nghịch biến trên .
Suy ra, hàm số nghịch biến [ − 1; 1].
.
.
Theo đề bài ta có: y1 − y2 = 8
⇔ m2 − 2m + 1 = 0 ⇔ m = 1.
Chọn khẳng định đúng
Hàm số f(x) có tập xác định ℝ và có đồ thị như hình vẽ
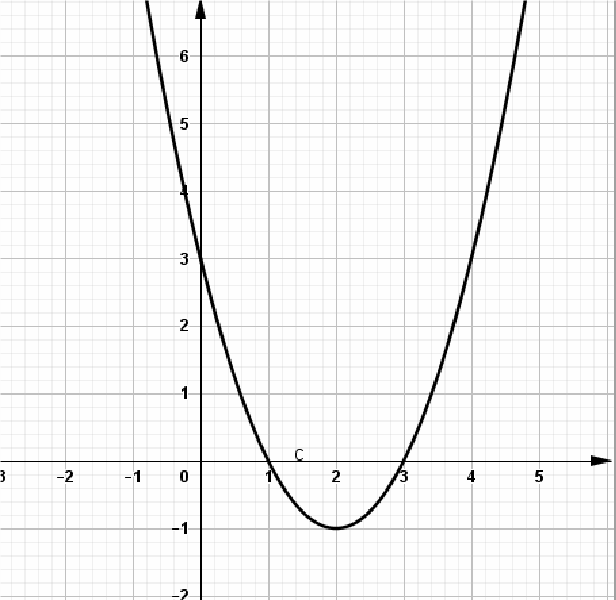
Mệnh đề nào sau đây đúng ?
Nhìn vào đồ thị hàm số ta có:
Đồ thị hàm số cắt trục hoành tại hai điểm M(1; 0), N(3; 0) ⇒ MN = 2 . Suy ra Đồ thị hàm số cắt trục hoành theo một dây cung có độ dài bằng 2là đúng.
Tính giá trị hàm số tại điểm
Cho hàm số ![f(x) =
\left\{ \begin{matrix}
\frac{2x + 3}{x + 1} & khi & x \geq 0 \\
\frac{\sqrt[3]{2 + 3x}}{x - 2} & khi & - 2 \leq x < 0 \\
\end{matrix} ight.](/data/image/holder.png) . Ta có kết quả nào sau đây đúng?
. Ta có kết quả nào sau đây đúng?
;
.
Tìm công thức hàm số bậc hai
Đồ thị hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
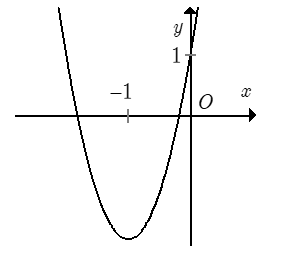
Nhận xét:
Parabol có bề lõm hướng lên.
Parabol cắt trục hoành tại 2 điểm phân biệt có hoành độ âm. Xét các đáp án, đáp án y = 3x2 + 6x + 1 thỏa mãn.
Chọn khẳng định đúng
Xét sự biến thiên của hàm số ![]() trên khoảng (0;+∞). Khẳng định nào sau đây đúng?
trên khoảng (0;+∞). Khẳng định nào sau đây đúng?
Ta có
Với mọi x1, x2 ∈ (0;+∞) và x1 < x2. Ta có .
Suy ra nghịch biến trên (0;+∞).
Tìm khoảng đồng biến nghịch biến
Hàm số ![]() đồng biến và nghịch biến trên khoảng nào?
đồng biến và nghịch biến trên khoảng nào?
Ta có hàm số có
=> Hàm số nghịch biến trên khoảng , đồng biến trên khoảng
Tìm tập xác định
Cho hàm số:  . Tập xác định của hàm số là tập hợp nào sau đây?
. Tập xác định của hàm số là tập hợp nào sau đây?
Với x ≤ 0 ta có: xác định với mọi x ≠ 1 nên xác định với mọi x ≤ 0.
Với x > 0 ta có: xác định với mọi x ≥ − 2 nên xác định với mọi x > 0.
Vậy tập xác định của hàm số là D = ℝ.
Tìm m thỏa mãn điều kiện
Tìm m để Parabol (P) : y = x2 − 2(m+1)x + m2 − 3 cắt trục hoành tại 2 điểm phân biệt có hoành độ x1, x2 sao cho x1.x2 = 1.
Phương trình hoành độ giao điểm của (P) với trục hoành: x2 − 2(m+1)x + m2 − 3 = 0 (1).
Parabol (P) cắt trục hoành tại 2 điểm phân biệt có hoành độ x1, x2 sao cho x1.x2 = 1
⇔ (1) có 2 nghiệm phân biệt x1, x2 thỏa x1.x2 = 1
.
Tìm hàm số bậc hai
Trong các hàm số sau, hàm số nào là hàm số bậc hai?
Đáp án là đáp án đúng vì hàm số bậc hai có dạng
Tính giá trị hàm số tại điểm
Cho hàm số  . Tính P = f(2) + f(−2).
. Tính P = f(2) + f(−2).
Ta có: .
Chọn khẳng định đúng
Xét tính đồng biến, nghịch biến của hàm số f(x) = x2 − 4x + 5 trên các khoảng (−∞; 2) và (2; +∞). Khẳng định nào sau đây đúng?
Xét f(x) = x2 − 4x + 5.
TXĐ: D = ℝ.
Tọa độ đỉnh I(2; 1).
Hàm số nghịch biến trên (−∞; 2), đồng biến trên (2; +∞).
Chọn khẳng định đúng
Hàm số y = x2 − 4x + 11 đồng biến trên khoảng nào trong các khoảng sau đây?
Ta có bảng biến thiên:

Từ bảng biến thiên ta thấy, hàm số đồng biến trên khoảng![]() (2;+∞).
(2;+∞).
Trục đối xứng của hàm số bậc hai
Trong các hàm số sau, hàm số nào có đồ thị nhận đường x = 1 làm trục đối xứng?
Ta có đáp án có:
Vậy x = 1 là trục đối xứng của đồ thị hàm số .
Tính tỉ lệ biết chữ của phụ nữ
Theo tài liệu dân số và phát triển của Tổng cục dân số và kế hoạch hóa gia đình thì:
Dựa trên số liệu về dân số, kinh tế, xã hội của 85 nước trên thế giới, người ta xây dựng được hàm nêu lên mối quan hệ giữa tuổi thọ trung bình của phụ nữ (y) và tỷ lệ biết chữ của họ (x) như sau: ![]() . Trong đó y là số năm (tuổi thọ), x là tỷ lệ phần trăm biết chữ của phụ nữ. Theo báo cáo của Bộ Giáo dục và Đào tạo năm học 2015 ‒ 2016, tỷ lệ biết chữ đã đạt 96,83% trong nhóm phụ nữ Việt Nam tuổi từ 15 đến 60. Hỏi với tỉ lệ biết chữ của phụ nữ Việt Nam như trên thì nhóm này có tuổi thọ bao nhiêu?
. Trong đó y là số năm (tuổi thọ), x là tỷ lệ phần trăm biết chữ của phụ nữ. Theo báo cáo của Bộ Giáo dục và Đào tạo năm học 2015 ‒ 2016, tỷ lệ biết chữ đã đạt 96,83% trong nhóm phụ nữ Việt Nam tuổi từ 15 đến 60. Hỏi với tỉ lệ biết chữ của phụ nữ Việt Nam như trên thì nhóm này có tuổi thọ bao nhiêu?
Thay x = 96,83 vào công thức y = 47,17 + 0,307x ta được:
y = 47,17 + 0,307. 96,83 = 47,17 + 29,72 = 76,89 (năm)
Vậy nhóm này có tuổi thọ 76,89 tuổi.
Tìm số giá trị m thỏa mãn điều kiện
Cho hàm số bậc nhất y = (m2−4m−4)x + 3m − 2 có đồ thị là (d). Tìm số giá trị nguyên dương của m để đường thẳng (d) cắt trục hoành và trục tung lần lượt tại hai điểm A, B sao cho tam giác OAB là tam giác cân (O là gốc tọa độ).
Đường thẳng (d) tạo với trục hoành và trục tung một tam giác OAB là tam giác vuông cân ⇔ đường thẳng (d) tạo với chiều dương trục hoành bằng 45∘ hoặc 135∘⇔ hệ số góc tạo của (d) bằng 1 hoặc
.
Thử lại: m = 5 thì d không đi qua O.
Vậy có duy nhất một giá trị m = 5 nguyên dương thỏa ycbt.
Tìm m thỏa mãn điều kiện
Cho parabol (P) : y = x2 − 4x + 3 và đường thẳng d : y = mx + 3. Tìm tất cả các giá trị thực của m để d cắt (P) tại hai điểm phân biệt A, B sao cho diện tích tam giác OAB bằng ![]() .
.
Phương trình hoành độ giao điểm của (P) và d là x2 − 4x + 3 = mx + 3
.
Để d cắt (P) tại hai điểm phân biệt A, B khi và chỉ khi 4 + m ≠ 0 ⇔ m ≠ − 4.
Với .
Với .
Gọi H là hình chiếu của B lên OA. Suy ra BH = |xB| = |4+m|.
Theo giả thiết bài toán, ta có
.
Xác định hàm số bậc hai
Hàm số nào sau đây có đỉnh ![]() ?
?
Hàm số có các hệ số a = 1, b = ‒2, c = 1 nên có tọa độ đỉnh
Chọn khẳng định sia
Cho hàm số y = − x2 + 4x + 1. Khẳng định nào sau đây sai?
Hàm số y = ax2 + bx + c với a < 0 nghịch biến trên khoảng , đồng biến trên khoảng
.
Áp dụng: Ta có Do đó hàm số nghịch biến trên khoảng (2;+∞) và đồng biến trên khoảng (−∞;2). Do đó Hàm số nghịch biến trên khoảng (4;+∞) và đồng biến trên khoảng (−∞;4) sai. Chọn đáp án này.
Đáp án Trên khoảng (−∞;−1) hàm số đồng biến đúng vì hàm số đồng biến trên khoảng (−∞;2) thì đồng biến trên khoảng con (−∞;−1).
Đáp án Trên khoảng (3;+∞) hàm số nghịch biến đúng vì hàm số nghịch biến trên khoảng (2;+∞) thì nghịch biến trên khoảng con (3;+∞).
Tìm tập xác định
Tìm tập xác định của hàm số ![]() .
.
Điều kiện xác định: .
Vậy .
Tìm m thỏa mãn điều kiện
Tìm giá trị thực của tham số m để parabol (P) : y = mx2 − 2mx − 3m − 2 (m≠0) có đỉnh thuộc đường thẳng y = 3x − 1.
Hoành độ đỉnh của (P) là .
Suy ra tung độ đỉnh y = − 4m − 2. Do đó tọa độ đỉnh của (P) là I(1;−4m−2).
Theo giả thiết, đỉnh I thuộc đường thẳng y = 3x − 1 nên − 4m − 2 = 3.1 − 1 ⇔ m = − 1.
Tìm m thỏa mãn điều kiện
Đồ thị hàm số y = x − 2m + 1 tạo với hệ trục tọa độ Oxy tam giác có diện tích bằng ![]() . Khi đó m bằng
. Khi đó m bằng
Gọi: A, B lần lượt là giao điểm của đồ thị hàm số y = x − 2m + 1 với trục hoành và trục tung
Suy ra A(2m−1; 0); B(0; 1−2m).
Theo giả thiết thì tam giác có diện tích bằng là tam giác OAB vuông tại O.
Do đó:
⇔ OA.OB = 25 ⇔ |2m−1|.|1−2m| = 25
⇔ |2m−1|.|2m−1| = 25
⇔ (2m−1)2 = 25
.
Tìm tập xác định
Tập xác định của hàm số ![]() là
là
Hàm số xác định khi .
Vậy tập xác định của hàm số là D = (1; 3].
Tìm đồ thị hàm số thỏa mãn
Đồ thị của hàm số ![]() là hình nào?
là hình nào?
Đồ thị hàm số cắt trục hoành tại điểm (4;0) và cắt trục tung tại điểm (0;2) nên chọn đáp án đồ thị hàm số đi qua 2 điểm này.
Tìm hàm số nghịch biến
Trong các hàm số sau, hàm số nào nghịch biến trên ℝ?
Hàm số y = ax + b với a ≠ 0 nghịch biến trên ℝ khi và chỉ khi a < 0.
Tìm tập xác định
Tập xác định của hàm số ![]() là
là
Ta có 9 − x2 ≥ 0 ⇔ (3−x)(3+x) ≥ 0 ⇔ − 3 ≤ x ≤ 3.
Hàm số xác định khi và chỉ khi
. Vậy x ∈ [ − 3; 3] ∖ {2}.
Chọn khẳng định đúng
Cho hàm số y = x2 − 2x + 3. Chọn câu đúng.
Ta có a = 1 > 0, b = − 2, c = 3 nên hàm số có đỉnh là I(1;2). Từ đó suy ra hàm số nghịch biến trên khoảng (−∞;1) và đồng biến trên khoảng (1;+∞).
Xác định tam thức bậc hai
Bảng xét dấu sau đây là của tam thức bậc hai nào?

Từ bảng xét dấu ta có:
có hai nghiệm phân biệt
và
khi
Do đó
Chọn khẳng định đúng
Chọn khẳng định đúng?
Lí thuyết định nghĩa hàm số đồng biến, nghịch biến: Hàm số y = f(x) được gọi là đồng biến trên K nếu ∀x1; x2 ∈ K, x1 < x2 ⇒ f(x1) < f(x2).
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
