VnDoc.com Lớp 10 Khóa học Lớp 10 Toán 10 - Chân trời sáng tạo

Đóng

Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm

Mua VnDoc PRO chỉ từ 79.000đ

Đóng

Bạn cần đăng nhập tài khoản Thành viên VnDoc để:

- Xem đáp án

- Nhận 1 lần làm bài trắc nghiệm miễn phí!

Đăng nhập

Đề kiểm tra 45 phút Chương 7 Bất phương trình bậc hai một ẩn

Mô tả thêm:

Đề kiểm tra 45 phút Toán 10 Chương 7 Bất phương trình bậc hai một ẩn sách Chân trời sáng tạo giúp bạn học tổng hợp lại kiến thức của cả nội dung chương. Cùng nhau luyện tập nha!

Thời gian làm: 45 phút
Số câu hỏi: 40 câu
Số điểm tối đa: 40 điểm
Tài khoản: Đăng nhập

Trước khi làm bài bạn hãy

1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
4 Căn chỉnh thời gian làm từng câu một cách hợp lý

Bắt đầu làm bài

Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay

Câu 1: Nhận biết
Tính số nghiệm của phương trình

Số nghiệm của phương trình $\sqrt{8-x^{2}}=\sqrt{x+2}$ là
- A.
  0
- B.
  1
- C.
  2
- D.
  3
Điều kiện: $\left\{ {\begin{array}{*{20}{c}} {8 - {x^2} \geqslant 0} \\ {x + 2 \geqslant 0} \end{array}} ight.$
Phương trình tương đương:
$\begin{gathered} \sqrt {8 - {x^2}} = \sqrt {x + 2} \hfill \\ \Leftrightarrow 8 - {x^2} = x + 2 \hfill \\ \Leftrightarrow - {x^2} - x + 6 = 0 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 2} \\ {x = - 3} \end{array}} ight. \hfill \\ \end{gathered}$
Kết hợp điều kiện ta được: $x=2$ thỏa mãn điều kiện
Vậy phương trình đã cho có một nghiệm.
Câu 2: Thông hiểu
Tìm số nghiệm của phương trình

Phương trình: $x^{2} + 5x + 2 + 2\sqrt{x^{2} + 5x + 10} =0$ có mấy nghiệm ?
- A.
  1
- B.
  3
- C.
  2
- D.
  4
Điều kiện xác định x² + 5x + 10 ≥ 0 ⇔ x ∈ ℝ.
Khi đó phương trình $\Leftrightarrow x^{2}+ 5x + 10 + 2\sqrt{x^{2} + 5x + 10} - 8 = 0$
$\Leftrightarrow \left\lbrack\begin{matrix}\sqrt{x^{2} + 5x + 10} = 2 \\\sqrt{x^{2} + 5x + 10} = - 4 \\\end{matrix} ight.$ $\Leftrightarrow \sqrt{x^{2} + 5x + 10} =2$
$\Leftrightarrow x^{2} + 5x + 6 = 0\Leftrightarrow \left\lbrack \begin{matrix}x = - 3 \\x = - 2 \\\end{matrix} ight.$ .
Vậy phương trình có hai nghiệm.
Câu 3: Thông hiểu
Tìm nghiệm của phương trình

Phương trình: $\sqrt{x+2}=4-x$ có bao nhiêu nghiệm?
- A.
  0
- B.
  1
- C.
  2
- D.
  3
Điều kiện: $x + 2 \geqslant 0 \Leftrightarrow x \geqslant - 2$
$\begin{matrix} \sqrt {x + 2} = 4 - x \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {4 - x \geqslant 0} \\ {x + 2 = {{\left( {4 - x} ight)}^2}} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \leqslant 4} \\ {x + 2 = 16 - 8x + {x^2}} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \leqslant 4} \\ {{x^2} - 9x + 14 = 0} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \leqslant 4} \\ {\left[ {\begin{array}{*{20}{c}} {x = 2\left( {tm} ight)} \\ {x = 7\left( {ktm} ight)} \end{array}} ight.} \end{array}} ight. \hfill \\ \end{matrix}$
Kết hợp với điều kiện ta được $x=2$ thỏa mãn
Vậy nghiệm của phương trình là $x=2$
Câu 4: Nhận biết
Tổng các nghiệm của phương trình là

Tổng các nghiệm của phương trình $\sqrt{x^{4} - 2x^{2} + 1} + x = 1$ là bao nhiêu?
- A.
  $- 2$ .
- B.
  $1$ .
- C.
  2.
- D.
  $- 1$ .
$\sqrt{x^{4} - 2x^{2} + 1} + x = 1\Leftrightarrow \sqrt{x^{4} - 2x^{2} + 1} = 1 - x$ $\Leftrightarrow\left\{ \begin{matrix}1 - x \geq 0 \\\left( x^{2} - 1 ight)^{2} = (1 - x)^{2} \\\end{matrix} ight.$ $\ \Leftrightarrow \left\{ \begin{matrix}x \leq 1 \\(x - 1)^{2}x(x - 2) = 0 \\\end{matrix} ight.$ $\ \Leftrightarrow \left\{ \begin{matrix}x \leq 1 \\\left\lbrack \begin{matrix}x = 1 \\x = 0 \\x = - 2 \\\end{matrix} ight.\ \\\end{matrix} ight.$ $\ \Leftrightarrow \left\lbrack \begin{matrix}x = 1 \\x = 0 \\x = - 2 \\\end{matrix} ight.$ .

Vậy tổng các nghiệm của phương trình là $- 1$ .
Câu 5: Nhận biết
Tìm x thỏa mãn

Cho tam thức bậc hai f(x) = 5x − x² − 6. Tìm x để f(x) ≥ 0.
- A.
  x ∈ [2; 3].
- B.
  x ∈ (−∞;2]∪[3;+∞).
- C.
  x ∈ (2;3).
- D.
  x ∈ (−∞;2) ∪ (3;+∞).
$f(x) = 5x - x^{2} - 6 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 2 \\ x = 3 \\ \end{matrix} ight.$

Dựa vào bảng xét dấu, ta chọn đáp án x ∈ [2; 3].
Câu 6: Nhận biết
Tam thức bậc hai nhận giá trị âm khi và chỉ khi

Tam thức bậc hai f(x) = − x² − 1 nhận giá trị âm khi và chỉ khi
- A.
  x ∈ (−∞;−1) ∪ (1;+∞).
- B.
  x ∈ [ − 1; 1].
- C.
  x ∈ (−∞;−1]∪[1;+∞).
- D.
  x ∈ ℝ.
f(x) = − x² − 1 = 0 vô nghiệm

Dựa vào bảng xét dấu, ta chọn đáp án x ∈ ℝ.
Câu 7: Thông hiểu
Chọn khẳng định đúng

Cho hàm số y = f(x) có đồ thị như hình vẽ. Hãy so sánh f(2017) với số 0.
- A.
  f(2017) < 0.
- B.
  f(2017) > 0.
- C.
  f(2017) = 0.
- D.
  Không so sánh được f(2017) với số 0.
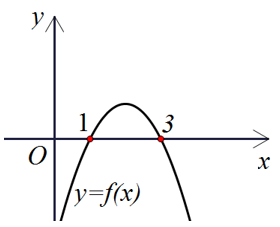
Nhìn đồ thị, ta thấy đồ thị y = f(x) cắt trục hoành tại 2 điểm x = 1, x = 3 nên Δ > 0, dựa vào hình dạng parabol nên suy ra a < 0 và ta có bảng xét dấu như sau:

Dựa vào bảng xét dấu thì f(x) < 0 khi x < 1 ∨ x > 3. Mà 2017 > 3 nên f(2017) < 0.
Câu 8: Thông hiểu
Tìm số nghiệm của phương trình

Số nghiệm của phương trình: $\sqrt{x - 4}\left( x^{2} - 3x + 2 ight) = 0$ là:
- A.
  4.
- B.
  3.
- C.
  1.
- D.
  2.
$\sqrt{x - 4}\left( x^{2} - 3x + 2ight) = 0$
$\Leftrightarrow \left\lbrack\begin{matrix}x - 4 = 0 \\\left\{ \begin{matrix}x - 4 > 0 \\x^{2} - 3x + 2 = 0 \\\end{matrix} ight.\ \\\end{matrix} ight.$
$\Leftrightarrow \left\lbrack\begin{matrix}x = 4 \\\left\{ \begin{matrix}x > 4 \\\left\lbrack \begin{matrix}x = 1 \\x = 2 \\\end{matrix} ight.\ \\\end{matrix} ight.\ \\\end{matrix} ight.\ \Leftrightarrow x = 4$ .
Vậy phương trình có một nghiệm.
Câu 9: Nhận biết
Tìm tập nghiệm của bất phương trình

Tập nghiệm S của bất phương trình $x^{2} + x - 12 < 0$ là:
- A.
  S = (−4;3)
- B.
  S = (4;+∞)
- C.
  S = (3;+∞)
- D.
  S = ∅
Ta có: $x^{2} + x - 12 < 0 \Leftrightarrow -4< x <3$ .
Suy ra $S = (-4;3)$ .
Câu 10: Thông hiểu
Tìm tập xác định

Tìm tập xác định D của hàm số $y = \sqrt{x^{2} + 2x + 3} + \frac{1}{\sqrt{5 - 2x}}.$
- A.
  $D = \left\lbrack \frac{5}{2}; + \ \infty ight).$
- B.
  $D = \left( - \ \infty;\frac{5}{2} ightbrack.$
- C.
  $D = \left( \frac{5}{2}; + \ \infty ight).$
- D.
  $D = \left( - \ \infty;\frac{5}{2} ight).$
Hàm số xác định khi và chỉ khi $\left\{ \begin{matrix} x^{2} + 2x + 3 \geq 0 \\ 5 - 2x > 0 \\ \end{matrix} ight.\ .$

Phương trình x² + 2x + 3 = 0 ⇔ x ∈ ⌀ và $5 - 2x = 0 \Leftrightarrow x = \frac{5}{2}.$

Bảng xét dấu

Dựa vào bảng xét dấu ta thấy $\left\{ \begin{matrix} x^{2} + 2x + 3 \geq 0 \\ 5 - 2x > 0 \\ \end{matrix} ight.\ \Leftrightarrow x \in \left( \ - \infty;\frac{5}{2} ight).$

Vậy tập xác định của hàm số là $D = \left( \ - \infty;\frac{5}{2} ight).$
Câu 11: Nhận biết
Tìm tập nghiệm của bất phương trình

Tập nghiệm của bất $\sqrt{2}x^{2}-(\sqrt{2}+1)x+1<0$ là:
- A.
  $(\frac{\sqrt{2}}{2};1)$
- B.
  ∅
- C.
  $[\frac{\sqrt{2}}{2};1]$
- D.
  $(\frac{-∞;\sqrt{2}}{2})\cup (1;+∞)$
Ta có: $\sqrt{2}x^{2}-(\sqrt{2}+1)x+1<0 \Leftrightarrow \frac{\sqrt2}2 < x <1$ .
Vậy $D=(\frac{\sqrt{2}}{2};1)$
Câu 12: Vận dụng cao
Tìm số nghiệm của phương trình

Phương trình $2x^{2} + x + 3 = 3x\sqrt{x + 3}$ có mấy nghiệm ?
- A.
  2.
- B.
  1.
- C.
  0.
- D.
  3.
Đặt $t = \sqrt{x + 3}\ \ \ (t \geq 0)$ . Phương trình đã cho trở thành:

$\begin{matrix} t^{2} - 3xt + 2x^{2} = 0 \Leftrightarrow (t - x)(t - 2x) = 0 \\ \Leftrightarrow \left\lbrack \begin{matrix} t = x \\ t = 2x \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} \sqrt{x + 3} = x \\ \sqrt{x + 3} = 2x \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} x = \frac{- 1 + \sqrt{13}}{2} \\ x = 1 \\ \end{matrix} ight.\ . \\ \end{matrix}$

Vậy phương trình có 2 nghiệm.
Câu 13: Nhận biết
Số nghiệm của phương trình là

Số nghiệm của phương trình $x - \sqrt{3x + 4} = 2$ là:
- A.
  $1$ .
- B.
  $2$ .
- C.
  $3$ .
- D.
  $0$ .
$x - \sqrt{3x + 4} = 2 \Leftrightarrow\sqrt{3x + 4} = x - 2$ $\Leftrightarrow \left\{ \begin{matrix}x - 2 \geq 0 \\3x + 4 = (x - 2)^{2} \\\end{matrix} ight.$ $\ \Leftrightarrow \left\{ \begin{matrix}x \geq 2 \\3x + 4 = x^{2} - 4x + 4 \\\end{matrix} ight.$ $\ \Leftrightarrow \left\{ \begin{matrix}x \geq 2 \\x^{2} - 7x = 0 \\\end{matrix} ight.$ $\ \Leftrightarrow \left\{ \begin{matrix}x \geq 2 \\\left\lbrack \begin{matrix}x = 0 \\x = 7 \\\end{matrix} ight.\ \\\end{matrix} ight.\ \Leftrightarrow x = 7$ .

Vậy phương trình có 1 nghiệm.
Câu 14: Nhận biết
Tìm nghiệm của phương trình

Nghiệm của phương trình: $\sqrt{x - 2} = \sqrt{2 - x}$ là bao nhiêu?
- A.
  $2$
- B.
  $- 2$
- C.
  $3$
- D.
  $1$
Điều kiện: $\left\{ \begin{matrix} x - 2 \geq 0 \\ 2 - x \geq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x \geq 2 \\ x \leq 2 \\ \end{matrix} ight.\ \Leftrightarrow x = 2$ .

Thay $x = 2$ vào phương trình ta được $0 = 0$ hay $x = 2$ là nghiệm của phương trình.
Câu 15: Nhận biết
Chọn khẳng định đúng

Tìm khẳng định đúng trong các khẳng định sau?
- A.
  f(x) = 3x² − 5 là tam thức bậc hai.
- B.
  f(x) = 2x − 4 là tam thức bậc hai.
- C.
  f(x) = 3x³ + 2x − 1 là tam thức bậc hai.
- D.
  f(x) = x⁴ − x² + 1 là tam thức bậc hai.
Tam thức bậc 2 là biểu thức f(x) có dạng ax²+ bx + c (a≠0).

f(x) = 3x² − 5 là tam thức bậc 2 với a = 3, b = 0, c = − 5.
Câu 16: Nhận biết
Phương trình có bao nhiêu nghiệm?

Phương trình $\sqrt{2x^{2} - 5x + 2} = \sqrt{6 - 3x}$ có bao nhiêu nghiệm?
- A.
  $1$ .
- B.
  $0$ .
- C.
  $3$ .
- D.
  $2$ .
$\sqrt{2x^{2} - 5x + 2} = \sqrt{6 - 3x}\Leftrightarrow \left\{ \begin{matrix}6 - 3x \geq 0 \\2x^{2} - 5x + 2 = 6 - 3x \\\end{matrix} ight.$ $\ \Leftrightarrow \left\{ \begin{matrix}x \leq 2 \\2x^{2} - 2x - 4 = 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x \leq 2 \\\left\lbrack \begin{matrix}x = - 1 \\x = 2 \\\end{matrix} ight.\ \\\end{matrix} ight.$ $\ \Leftrightarrow \left\lbrack \begin{matrix}x = - 1 \\x = 2 \\\end{matrix} ight.$ .

Vậy phương trình có 2 nghiệm.
Câu 17: Vận dụng
Tính số nghiệm của phương trình

Số nghiệm của phương trình $\sqrt{7 - x} + \sqrt{x - 5} = x^{2} - 12x +38$ là:
- A.
  0.
- B.
  1.
- C.
  2.
- D.
  3.
ĐK: x ∈ [5; 7]
Đặt t = x − 6 , t ∈ [ − 1; 1].
Phương trình trở thành $\sqrt{1 - t} +\sqrt{t - 1} = t^{2} + 2 \Leftrightarrow 2 + 2\sqrt{1 - t^{2}} = \left(t^{2} + 2 ight)^{2}(*)$ .
Ta có VT(*) ≤ 4, VP(*) ≥ 4 nên (*) ⇔ VT(*) = VP(*) = 4 ⇔ t = 0 ⇒ x = 6(TM).
Vậy phương trình có một nghiệm.
Câu 18: Vận dụng cao
Tính tổng các nghiệm của phương trình

Tổng các nghiệm của phương trình $\sqrt{4x^{2} - 1} - \sqrt{2x + 1} = 1 + x - 2x^{2}$ là:
- A.
  2.
- B.
  $\frac{1}{2}$ .
- C.
  $\frac{3}{2}$ .
- D.
  $- \frac{1}{2}$ .
Đặt $\sqrt{4x^{2} - 1} = a;\sqrt{2x + 1} = b(a,b \geq 0)$ .

Ta có $1 + x - 2x^{2} = - \frac{1}{2}(4x^{2} - 1) + \frac{1}{2}(2x + 1)$ .

Phương trình trở thành $a - b = \frac{1}{2}\left( b^{2} - a^{2} ight) \Leftrightarrow a = b$

Thay vào ta được $x = 1;x = - \frac{1}{2}$ . Vậy tổng các nghiệm của phương trình là $\frac{1}{2}$ .
Câu 19: Nhận biết
Tìm m để biểu thức là tam thức bậc hai

Xác định m để biểu thức $f(x) = (m + 2)x^{2} – 3mx + 1$ là tam thức bậc hai.
- A.
  m = 2
- B.
  m = – 2
- C.
  m ≠ 2
- D.
  m ≠ – 2
Để biểu thức $f(x) = (m + 2)x^{2} – 3mx + 1$ là tam thức bậc hai ta có:
$m + 2 e 0 \Leftrightarrow m e - 2$
Câu 20: Nhận biết
Tìm nghiệm của phương trình

Phương trình $\sqrt{4x^{2}-3}=x$ có nghiệm là:
- A.
  x = 1
- B.
  x = –1
- C.
  x = 1 hoặc x = –1
- D.
  Vô nghiệm.
Điều kiện: $4{x^2} - 3 \geqslant 0$
Phương trình tương đương:
$\begin{matrix} \sqrt {4{x^2} - 3} = x \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \geqslant 0} \\ {4{x^2} - 3 = {x^2}} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \geqslant 0} \\ {3{x^2} = 3} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \geqslant 0} \\ {\left[ {\begin{array}{*{20}{c}} {x = - 1\left( {ktm} ight)} \\ {x = 1\left( {tm} ight)} \end{array}} ight.} \end{array}} ight. \hfill \\ \end{matrix}$
Kết hợp với điều kiện ra được: $x=1$ thỏa mãn điều kiện
Vậy phương trình có nghiệm $x=1$
Câu 21: Thông hiểu
Tìm m thỏa mãn điều kiện

Cho f(x) = − 2x² + (m+2)x + m − 4. Tìm m để f(x) âm với mọi a, b, c > 0.
- A.
  − 14 < m < 2.
- B.
  − 14 ≤ m ≤ 2.
- C.
  − 2 < m < 14.
- D.
  m < − 14 hoặc m > 2.
Ta có $f(x)<0,\forall x\in R\Leftrightarrow(m+2)^2+8(m-4)<0$

$\Leftrightarrow m^2+12m-28<0\Leftrightarrow-14<m<2$ .
Câu 22: Vận dụng
Tính số nghiệm của phương trình

Phương trình $\sqrt{x} + \sqrt{9 - x} = \sqrt{- x^{2} + 9x +9}$ có mấy nghiệm ?
- A.
  1
- B.
  3
- C.
  2
- D.
  4
Điều kiện: 0 ≤ x ≤ 9
Bình phương hai vế phương trình đã cho ta được:
$\begin{matrix}x + 2\sqrt{9x - x^{2}} + 9 - x = - x^{2} + 9x + 9 \\\Leftrightarrow 2\sqrt{9x - x^{2}} = - x^{2} + 9x \\\end{matrix}$
Đặt $t = \sqrt{9x - x^{2}}\ \ \ \ (t \geq0)$ . PT trên trở thành: $2t = t^{2}\Leftrightarrow \left\lbrack \begin{matrix}t = 0 \\t = 2 \\\end{matrix} ight.$
Với $t = 0 \Rightarrow \sqrt{9x - x^{2}} =0 \Leftrightarrow \left\lbrack \begin{matrix}x = 0 \\x = 9 \\\end{matrix} ight.$ (TM)
Với $t = 2 \Rightarrow \sqrt{9x - x^{2}} =2 \Leftrightarrow \left\lbrack \begin{matrix}x = \frac{9 + \sqrt{65}}{2} \\x = \frac{9 - \sqrt{65}}{2} \\\end{matrix} ight.$ (TM)
Vậy phương trình có tập nghiệm là $S =\left\{ 0;9;\frac{9 \pm \sqrt{65}}{2} ight\}$ (3 nghiệm).
Câu 23: Nhận biết
Chọn khẳng định đúng

Tam thức bậc hai $f(x) = x^{2} + \left( 1 - \sqrt{3} ight)x - 8 - 5\sqrt{3}$ :
- A.
  Âm với mọi $x \in \left( - 2 - \sqrt{3};1 + 2\sqrt{3} ight)$ .
- B.
  Âm với mọi x ∈ ℝ.
- C.
  Dương với mọi x ∈ ℝ.
- D.
  Âm với mọi x ∈ (−∞;1).
$f(x) = x^{2} + \left( 1 - \sqrt{3} ight)x - 8 - 5\sqrt{3} = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 2 - \sqrt{3} \\ x = 1 + 2\sqrt{3} \\ \end{matrix} ight.$

Dựa vào bảng xét dấu, chọn đáp án Âm với mọi $x \in \left( - 2 - \sqrt{3};1 + 2\sqrt{3} ight)$ .
Câu 24: Thông hiểu
Tìm tập nghiệm của phương trình

Tập nghiệm của phương trình $(x^{2} - 5x + 4)\sqrt{x - 2} = 0$ là:
- A.
  S = {1;2;4}.
- B.
  S = {2;4}.
- C.
  S = {1;4}.
- D.
  S = {1;2}
$\left( x^{2} - 5x + 4 ight)\sqrt{x -2} = 0 \Leftrightarrow \left\lbrack \begin{matrix}x = 2 \\\left\{ \begin{matrix}x > 2 \\x^{2} - 5x + 4 = 0 \\\end{matrix} ight.\ \\\end{matrix} ight.$
$\Leftrightarrow \left\lbrack\begin{matrix}x = 2 \\\left\{ \begin{matrix}x > 2 \\\left\lbrack \begin{matrix}x = 1 \\x = 4 \\\end{matrix} ight.\ \\\end{matrix} ight.\ \\\end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix}x = 2 \\x = 4 \\\end{matrix} ight.$ .
Vậy S = {2;4}.
Câu 25: Nhận biết
Chọn kết luận đúng

Cho tam thức bậc hai $f(x) = {x^2} - 10x + 2$ . Kết luận nào sau đây đúng?
- A.
  $f(–2) < 0$
- B.
  $f(1) > 0$
- C.
  $f(–2) > 0$
- D.
  $f(1) = 0$
Ta có:
$\begin{matrix}f\left( { - 2} ight) = {\left( { - 2} ight)^2} - 10.\left( { - 2} ight) + 2 = 26 > 0 \hfill \\ f\left( 1 ight) = {\left( 1 ight)^2} - 10.\left( 1 ight) + 2 = - 7 < 0 \hfill \\ \end{matrix}$
Vậy khẳng định đúng là $f(–2) > 0$ .
Câu 26: Vận dụng
Tìm tập xác định của hàm số

Tập xác định của hàm số $y = \frac{mx}{\left( 2m^{2} + 1 ight)x^{2} - 4mx + 2}$ là:
- A.
  D = ℝ.
- B.
  D = ℝ ∖ {1}
- C.
  D = (−∞ ; 1)
- D.
  D = (1 ; +∞)
ĐKXĐ: (2m²+1)x² − 4mx + 2 ≠ 0.

Xét tam thức bậc hai f(x) = (2m²+1)x² − 4mx + 2.

Ta có a = 2m² + 1 > 0,  Δ′ = 4m² − 2(2m²+1) = − 2 < 0.

Suy ra với mọi m ta có f(x) = (2m²+1)x² − 4mx + 2 > 0  ∀x ∈ ℝ.

Do đó với mọi m ta có (2m²+1)x² − 4mx + 2 ≠ 0,  ∀x ∈ ℝ.

Vậy tập xác định của hàm số là D = ℝ.
Câu 27: Vận dụng cao
Tìm khẳng định đúng

Biết phương trình $(x + 5)(2 - x) = 3\sqrt{x^{2} + 3x}$ có 2 nghiệm x₁, x₂(x₁<x₂) . Khẳng định nào sau đây đúng?
- A.
  $x_{1} = \frac{1}{4}x_{2}$ .
- B.
  4x₁ + x₂ = 0.
- C.
  x₁ + 4x₂ = 0.
- D.
  x₁ = 4x₂.
Điều kiện:

x² + 3x ≥ 0⇔ $\left\lbrack \begin{matrix} x \leq - 3 \\ x \geq 0 \\ \end{matrix} ight.\ (1)$

phương trình $\Leftrightarrow x^{2} + 3x + 3\sqrt{x^{2} + 3x} - 10 = 0$ .

Đặt $t = \sqrt{x^{2} + 3x}$ , điều kiện t ≥ 0.

Phương trình trở thành t² + 3t − 10 = 0

⇔ $\left\lbrack \begin{matrix} t = 2(TM) \\ t = - 5(KTM) \\ \end{matrix} ight.$ ⇒ $\sqrt{x^{2} + 3x} = 2 \Leftrightarrow x^{2} + 3x - 4 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 = x_{2} \\ x = - 4 = x_{1} \\ \end{matrix} ight.$ , thoả mãn (1) ⇒ x₁ + 4x₂ = 0.
Câu 28: Thông hiểu
Tìm số nghiệm của phương trình

Phương trình $\sqrt{3x + 1} + \sqrt{5 - x} = 4$ có bao nhiêu nghiệm
- A.
  2.
- B.
  3.
- C.
  1.
- D.
  0.
Đkxđ: $- \frac{1}{3} \leq x \leq5$ .
$\sqrt{3x + 1} + \sqrt{5 - x} =4$
$\Leftrightarrow 2x + 6 + 2\sqrt{(3x +1)(5 - x)} = 16$
$\Leftrightarrow \sqrt{(3x + 1)(5 - x)} =5 - x$
$\Leftrightarrow \left\lbrack\begin{matrix}\sqrt{5 - x} = 0 \\\sqrt{3x + 1} = \sqrt{5 - x} \\\end{matrix} ight.$
$\Leftrightarrow \left\lbrack\begin{matrix}x = 5 \\3x + 1 = 5 - x \\\end{matrix} ight.$
$\Leftrightarrow \left\lbrack\begin{matrix}x = 5(TM) \\x = 1(TM) \\\end{matrix} ight.$ .
Vậy phương trình có hai nghiệm.
Câu 29: Nhận biết
Tam thức bậc hai nhận giá trị không âm khi và chỉ khi

Tam thức bậc hai f(x) = − x² + 3x − 2 nhận giá trị không âm khi và chỉ khi
- A.
  x ∈ (−∞;1) ∪ (2;+∞).
- B.
  x ∈ [1; 2].
- C.
  x ∈ (−∞;1]∪[2;+∞).
- D.
  x ∈ (1;2).
$f(x) = - x^{2} + 3x - 2 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = 2 \\ \end{matrix} ight.$

Dựa vào bảng xét dấu, ta chọn đáp ánx ∈ [1; 2] .
Câu 30: Nhận biết
Nhận biết bất phương trình bậc hai một ẩn

Bất phương trình nào sau đây là bất phương trình bậc hai một ẩn?
- A.
  $3x^{2} – 12x + 1 ≤ 0$
- B.
  $2x^{3} + 5 > 0$
- C.
  $x^{2} + x – 1 = 0$
- D.
  $–x + 7 > 0$
Bất phương trình bậc hai một ẩn là: $3x^{2} – 12x + 1 ≤ 0$
Câu 31: Thông hiểu
Chọn kết luận đúng

Tam thức bậc hai $f(x)=(1-\sqrt{2})x^{2}+(5-4\sqrt{2})x-3\sqrt{2}+6$
- A.
  Dương với mọi $x \in \mathbb{R}$
- B.
  Dương với mọi $x∈(-3;\sqrt{2})$
- C.
  Dương với mọi $x∈(-4;\sqrt{2})$
- D.
  Âm với mọi $x \in \mathbb{R}$
Ta có: $\Delta >0$ và $a=1-\sqrt2 <0$ .
Phương trình $f(x)=0$ có hai nghiệm là $x=-3$ và $x=\sqrt2$ .
Do đó $f(x)>0$ $\forall x ∈(-3;\sqrt{2})$ .
Câu 32: Thông hiểu
Tìm tập nghiệm của bất phương trình

Tập nghiệm $S$ của bất phương trình $5(x+1)−x(7−x)>−2x$ là:
- A.
  $S = \mathbb{R}$
- B.
  $S=(−\frac{5}{2};+∞)$
- C.
  $S=(−∞;\frac{5}{2})$
- D.
  $S = \varnothing$
Ta có: $5(x+1)−x(7−x)>−2x \Leftrightarrow x^2+5>0$ (hiển nhiên).
Vậy $S = \mathbb{R}$ .
Câu 33: Vận dụng
Tính số nghiệm của phương trình

Phương trình $(x -1)(x + 3) + 2(x - 1)\sqrt{\frac{x + 3}{x - 1}} = 8$ có mấy nghiệm ?
- A.
  2
- B.
  3
- C.
  1
- D.
  4
Điều kiện: $\left\lbrack \begin{matrix}x \leq - 3 \\x > 1 \\\end{matrix} ight.$
Đặt $t = (x - 1)\sqrt{\frac{x + 3}{x - 1}}\Rightarrow t^{2} = (x - 1)(x + 3)$ .
PT đã cho trở thành:
$t^{2} + 2t - 8 = 0 \Leftrightarrow\left\lbrack \begin{matrix}t = 2\ \ \\t = - 4\ \ \ \\\end{matrix} ight.$
Với t = 2 ta được
$\begin{matrix}(x - 1)\sqrt{\frac{x + 3}{x - 1}} = 2 \\\Rightarrow (x - 1)(x + 3) = 4 \Leftrightarrow \left\lbrack\begin{matrix}x = - 1 + 2\sqrt{2}(TM) \\x = - 1 - 2\sqrt{2}(L) \\\end{matrix} ight.\ \\\end{matrix}$
Với t = − 4 ta được ta được
$\begin{matrix}(x - 1)\sqrt{\frac{x + 3}{x - 1}} = - 4 \\\Rightarrow (x - 1)(x + 3) = 16 \Leftrightarrow \left\lbrack\begin{matrix}x = - 1 + 2\sqrt{5}(L) \\x = - 1 - 2\sqrt{5}(TM) \\\end{matrix} ight.\ \\\end{matrix}$
Vậy phương trình có hai nghiệm là $x = - 1+ 2\sqrt{2}$ ; $x = - 1 -2\sqrt{5}$ .
Câu 34: Vận dụng
Tìm m để bất phương trình vô nghiệm

Cho tam thức bậc hai $f(x) = \left( 2m^{2} + m - 6 ight)x^{2} + (2m - 3)x - 1$ . Tìm tất cả các giá trị thực của tham số m để bất phương trình $f(x) > 0$ vô nghiệm?
- A.
  $m \in \left( - \frac{5}{6};\frac{3}{2} ightbrack$
- B.
  $m \in \left( - \frac{5}{6};\frac{3}{2} ight)$
- C.
  $m \in \left\lbrack - \frac{5}{6};\frac{3}{2} ight)$
- D.
  $m \in \left\lbrack - \frac{5}{6};\frac{3}{2} ightbrack$
Bất phương trình: $f(x) > 0\ (*)$ vô nghiệm khi và chỉ khi

$\left( 2m^{2} + m - 6 ight)x^{2} + (2m - 3)x - 1 \leq 0,\forall x\mathbb{\in R}$

Xét $2m^{2} + m - 6 = 0 \Leftrightarrow \left\lbrack \begin{matrix} m = - 2 \\ m = \frac{3}{2} \\ \end{matrix} ight.$

Với $m = - 2$ thì (*) $\Leftrightarrow - 7x - 1 > 0 \Leftrightarrow x < - \frac{1}{7}$ loại giá trị $m = - 2$ .

Với $m = \frac{3}{2}$ thì bất phương trình (*) $\Leftrightarrow 0x - 1 < 0$ bất phương trình vô nghiệm, nhận giá trị $m = \frac{3}{2}$ .

Xét $2m^{2} + m - 6 eq 0$

$\left( 2m^{2} + m - 6 ight)x^{2} + (2m - 3)x - 1 \leq 0,\forall x\mathbb{\in R}$

$\Leftrightarrow \left\{ \begin{matrix} 2m^{2} + m - 6 < 0 \\ (2m - 3)^{2} - 4\left( 2m^{2} + m - 6 ight).( - 1) \leq 0 \\ \end{matrix} ight.$

$\Leftrightarrow \left\{ \begin{gathered} - 2 < m < \dfrac{3}{2} \hfill \\ - \dfrac{5}{6} \leqslant m \leqslant \frac{3}{2} \hfill \\ \end{gathered} ight. \Leftrightarrow - \frac{5}{6} \leqslant m < \frac{3}{2}$

Vậy $m \in \left\lbrack - \frac{5}{6};\frac{3}{2} ightbrack$ thì bất phương trình (*) vô nghiệm.
Câu 35: Nhận biết
Tổng các bình phương của các nghiệm là

Tổng các bình phương của các nghiệm của phương trình $(x - 1)(x - 3) + 3\sqrt{x^{2} - 4x + 5} - 2 = 0$ bằng bao nhiêu?
- A.
  $17$ .
- B.
  $4$ .
- C.
  $16$ .
- D.
  $8$ .
Ta có $(x - 1)(x - 3) + 3\sqrt{x^{2} - 4x + 5} - 2 = 0$

$\Leftrightarrow x^{2} - 4x + 5 +3\sqrt{x^{2} - 4x + 5} - 4 = 0$ $\Leftrightarrow \sqrt{x^{2} - 4x + 5} =1$

$\Leftrightarrow x^{2} - 4x + 5 = 1 \Leftrightarrow x^{2} - 4x + 4 = 0 \Leftrightarrow x = 2$ .

Tổng các bình phương của các nghiệm của phương trình là $4$ .
Câu 36: Nhận biết
Tam thức bậc hai dương khi và chỉ khi

Tam thức bậc hai $f(x) = x^{2} + \left( \sqrt{5} - 1 ight)x - \sqrt{5}$ nhận giá trị dương khi và chỉ khi
- A.
  $x \in \left( - \sqrt{5};1 ight).$
- B.
  $x \in \left( - \infty; - \sqrt{5} ight) \cup (1; + \infty).$
- C.
  $x \in \left( - \sqrt{5}; + \infty ight).$
- D.
  x ∈ (−∞;1).
$f(x) = x^{2} + \left( \sqrt{5} - 1 ight)x - \sqrt{5} = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - \sqrt{5} \\ \end{matrix} ight.$

Dựa vào bảng xét dấu, ta chọn đáp án $x \in \left( - \infty; - \sqrt{5} ight) \cup (1; + \infty).$
Câu 37: Thông hiểu
Tam thức bậc hai không âm khi nào

Tam thức bậc hai $f(x)=−x^{2}+3x−2$ nhận giá trị không âm khi và chỉ khi
- A.
  x ∈ (−∞;1)∪(2;+∞)
- B.
  x ∈ [1;2]
- C.
  x ∈ (−∞;1)∪(2;+∞)
- D.
  x ∈ (1;2)
Ta có: $\Delta >0$ và $a=-1<0$ .
Phương trình $f(x)=0$ có hai nghiệm phân biệt là $x=1;x=2$ .
Do đó, $f(x) \ge 0$ $x \in [1;2]$ .
Câu 38: Thông hiểu
Tìm tập nghiệm của phương trình

Tập nghiệm của phương trình $x + \sqrt{x - 1} = 2 + \sqrt{x - 1}$ là:
- A.
  S = {2}.
- B.
  S = {1}.
- C.
  S = {3}.
- D.
  S = ⌀.
Phương trình $x + \sqrt{x - 1} = 2 +\sqrt{x - 1} \Leftrightarrow \left\{ \begin{matrix}x \geq 1 \\x = 2 \\\end{matrix} ight.\ \Leftrightarrow x = 2$ .
Vậy S = {2}.
Câu 39: Vận dụng
Tìm tập xác định

Tìm tập xác định của hàm số $y = \frac{2x + 3m}{\sqrt{x^{2} + 2(1 - m)x + 2m^{2} + 3}}$ .
- A.
  D = (−2 ; 3)
- B.
  D = (−3 ; 2)
- C.
  D = (−2 ; +∞)
- D.
  D = ℝ
ĐKXĐ: x² + 2(1−m)x + 2m² + 3 > 0

Xét tam thức bậc hai f(x) = x² + 2(1−m)x + 2m² + 3

Ta có $\begin{matrix} a = 1 > 0,\ \ \Delta' = (1 - m)^{2} - \left( 2m^{2} + 3 ight) \\ = - m^{2} - 2m - 2 < 0 \\ \end{matrix}$

(Vì tam thức bậc hai f(m) = − m² − 2m − 2 có a_m = − 1 < 0, Δ′_m = − 1 < 0 )

Suy ra với mọi m ta có x² + 2(1−m)x + 2m² + 3 > 0, ∀x ∈ ℝ.

Vậy tập xác định của hàm số là D = ℝ.
Câu 40: Thông hiểu
Tìm m thỏa mãn điều kiện

Tìm m để f(x) = x² − 2(2m−3)x + 4m − 3 > 0, ∀x ∈ ℝ?
- A.
  $m > \frac{3}{2}$ .
- B.
  $m > \frac{3}{4}$ .
- C.
  $\frac{3}{4} < m < \frac{3}{2}$ .
- D.
  1 < m < 3.
f(x) = x² − 2(2m−3)x + 4m − 3 > 0, ∀x ∈ ℝ⇔Δ < 0 ⇔ 4m² − 16m + 12 < 0 ⇔ 1 < m < 3.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 7 Bất phương trình bậc hai một ẩn Kết quả

Thời gian làm bài: 00:00:00
Số câu đã làm: 0
Điểm tạm tính: 0
Điểm thưởng: 0
Tài khoản làm: Đăng nhập

Làm lại

Chia sẻ bởi:
Khang Anh

23 Bài viết đã được lưu

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Số điện thoại này đã được xác thực!

Bạn có thể dùng Sđt này đăng nhập tại đây!

Lỗi gửi SMS, liên hệ Admin

Sắp xếp theo

Xóa Đăng nhập để Gửi

Đề kiểm tra 45 phút Chương 7 Bất phương trình bậc hai một ẩn

Thời gian còn lại 45:00 Số câu đã làm 0/40

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

Chưa làm Đã làm

Làm lại Nộp bài

Tìm bài trong mục này

Chương 1: Mệnh đề và tập hợp
Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
Chương 3: Hàm số bậc hai và đồ thị
Chương 4: Hệ thức lượng trong tam giác
Chương 5: Vectơ
Đề kiểm tra học kì 1
Chương 6: Thống kê
Chương 7: Bất phương trình bậc hai một ẩn
Chương 8: Đại số tổ hợp
Đề thi giữa học kì 2
Chương 9: Phương pháp tọa độ trong mặt phẳng
Chương 10: Xác suất
Đề thi học kì 2

Lớp 10
Khóa học Lớp 10
Toán 10 - Chân trời sáng tạo

Toán 10 - Chân trời sáng tạo

Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 5
Đề thi giữa học kì 2 Toán 10 Chân trời sáng tạo (Đề 5)
Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 1
Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 4
Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 2
Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 3

Xem thêm

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Đề kiểm tra 45 phút Chương 7 Bất phương trình bậc hai một ẩn

Chúc mừng Bạn đã hoàn thành bài!

Toán 10 - Chân trời sáng tạo

Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 5

Đề thi giữa học kì 2 Toán 10 Chân trời sáng tạo (Đề 5)

Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 1

Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 4

Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 2

Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 3