Tính giá trị của biểu thức
Giá trị của ![]() là
là
Ta có:
.
Đề kiểm tra 15 phút Toán 10 Chương 4 Hệ thức lượng trong tam giác sách Chân trời sáng tạo giúp bạn học tổng hợp lại kiến thức của cả nội dung chương. Cùng nhau luyện tập nha!
Tính giá trị của biểu thức
Giá trị của ![]() là
là
Ta có:
.
Tính độ dài cạnh b
Cho tam giác ![]() có
có ![]() . Hỏi độ dài cạnh b bằng bao nhiêu?
. Hỏi độ dài cạnh b bằng bao nhiêu?
Áp dụng định lí sin:
.
Chọn đáp án đúng
Trong tam giác ABC ta có:
Áp dụng định lí sin trong tam giác ABC ta có:
Tính độ dài cạnh BC
Trong tam giác ABC có ![]() và
và ![]() . Tính độ dài cạnh BC.
. Tính độ dài cạnh BC.
Áp dụng định lí cosin cho tam giác ABC ta có:
Tính giá trị biểu thức
Giá trị biểu thức ![]() bằng:
bằng:
Ta có:
Tính giá trị của biểu thức
Cho biết ![]() . Giá trị của
. Giá trị của ![]() bằng bao nhiêu?
bằng bao nhiêu?
Ta có:
.
Tính số đo góc B
Cho ![]() thỏa mãn :
thỏa mãn : ![]() . Khi đó:
. Khi đó:
Ta có:
Chọn khẳng định đúng
Trong các khẳng định sau, khẳng định nào là đúng?
Ta có: . Vì
.
Chọn đẳng thức đúng
Trong các đẳng thức sau đây, đẳng thức nào đúng?
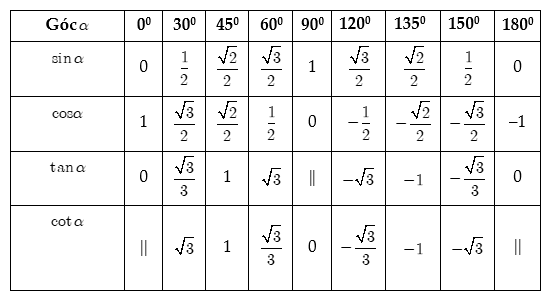
Giá trị lượng giác của góc đặc biệt.
Tính khoảng cách AB
Khoảng cách từ ![]() đến
đến ![]() không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm
không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm ![]() mà từ đó có thể nhìn được
mà từ đó có thể nhìn được ![]() và
và ![]() dưới một góc
dưới một góc ![]() . Biết
. Biết ![]() . Khoảng cách
. Khoảng cách ![]() bằng bao nhiêu?
bằng bao nhiêu?
Ta có:
Tính độ dài cạnh AC
Tam giác ![]() có
có ![]() . Gọi
. Gọi ![]() là trung điểm của
là trung điểm của ![]() . Biết
. Biết ![]() và
và ![]() . Tính độ dài cạnh
. Tính độ dài cạnh ![]() .
.
Hình vẽ minh họa:
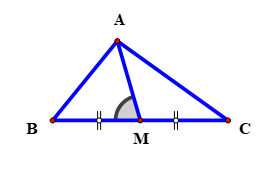
Trong tam giác ta có:
Ta có: và
là hai góc kề bù.
Trong tam giác ta có:
.
Chọn đẳng thức đúng
Trong các đẳng thức sau, đẳng thức nào đúng?
Đáp án đúng là sin(180° – α) = sin α
Chọn biểu thức tính độ dài đường trung tuyến tam giác
Độ dài trung tuyến ![]() ứng với cạnh
ứng với cạnh ![]() của
của ![]() bằng biểu thức nào sau đây?
bằng biểu thức nào sau đây?
Ta có:
.
Tính giá trị của biểu thức P
Cho góc ![]() thỏa mãn
thỏa mãn ![]() và
và ![]() Tính
Tính ![]()
Áp dụng , ta có
Ta có
Vì nên ta chọn
.
Thay vào
, ta được
.
Chọn đáp án đúng
Cho tam giác ![]() thỏa mãn:
thỏa mãn: ![]() . Khi đó:
. Khi đó:
Ta có:
Tính chiều dài hàng rào
Bà Sáu sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào ![]() là
là ![]() , chiều dài của hàng rào
, chiều dài của hàng rào ![]() là
là ![]() . Góc giữa hai hàng rào
. Góc giữa hai hàng rào ![]() và
và ![]() là
là ![]() (như hình vẽ).
(như hình vẽ).

Chiều dài hàng rào ![]() là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Áp dụng định li côsin ta
.
Suy ra .
Vậy chiều dài hàng rào là khoảng
.
Tính độ dài cạnh BC
Tam giác ![]() có
có ![]() và
và ![]() . Tính độ dài cạnh
. Tính độ dài cạnh ![]() .
.
Theo định lí hàm cosin, ta có
.
Tính chiều cao của tháp
Giả sử ![]() là chiều cao của tháp trong đó
là chiều cao của tháp trong đó ![]() là chân tháp. Chọn hai điểm
là chân tháp. Chọn hai điểm ![]() trên mặt đất sao cho ba điểm
trên mặt đất sao cho ba điểm ![]() và
và ![]() thẳng hàng. Ta đo được
thẳng hàng. Ta đo được ![]() ,
, ![]() .
.
Chiều cao ![]() của tháp gần với giá trị nào sau đây?
của tháp gần với giá trị nào sau đây?

Áp dụng định lí sin vào tam giác ta có
Ta có nên
Do đó
Trong tam giác vuông có
Tính độ dài cạnh b
Cho ![]() có
có ![]() Độ dài cạnh
Độ dài cạnh ![]() bằng:
bằng:
Ta có:
.
Tính giá trị lượng giác
Cho góc ![]() thỏa mãn
thỏa mãn ![]() và
và ![]() . Tính
. Tính ![]()
Ta có:
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
