Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 10 Khóa học Lớp 10 Toán 10 - Chân trời sáng tạo
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Đề thi học kì 1 Toán 10 Chân trời sáng tạo Đề 3

Mô tả thêm:

Mời các bạn học cùng thử sức với Đề thi học kì 1 môn Toán lớp 10 theo chương trình sách Chân trời sáng tạo nha!
  • Thời gian làm: 90 phút
  • Số câu hỏi: 45 câu
  • Số điểm tối đa: 45 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Bắt đầu làm bài
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
  • Câu 1: Nhận biết

    Tìm đẳng thức sai

    Trong các đẳng thức sau đây, đẳng thức nào sai?

    Vi \sin60^{0} + \cos60^{0} =\frac{\sqrt{3}}{2} + \frac{1}{2} = \frac{\sqrt{3} + 1}{2} \neq1 suy ra đẳng thức sai là: \sin60^{0} + \cos60^{0} = 1.

  • Câu 2: Thông hiểu

    Chọn kết luận đúng

    Cho hình bình hành ABCD, điểm M thoả mãn: \overrightarrow{MA} + \overrightarrow{MC} = \overrightarrow{AB}. Khi đó M là trung điểm của:

    Ta có \overrightarrow{MA} + \overrightarrow{MC} = 2\overrightarrow{MI} = \overrightarrow{AB}.

    Vậy M là trung điểm của AD.

  • Câu 3: Vận dụng cao

    Tìm m để phương trình có nghiệm duy nhất

    Cho \frac{x^{2} - 2(m + 1)x + 6m - 2}{\sqrt{x - 2}} = \sqrt{x - 2}(1). Với m là bao nhiêu thì (1) có nghiệm duy nhất

    ĐK x > 2

    \frac{x^{2} - 2(m + 1)x + 6m - 2}{\sqrt{x - 2}} = \sqrt{x - 2} \Rightarrow x^{2} - 2(m + 1)x + 6m - 2 = x - 2 \Leftrightarrow x^{2} - (2m + 3)x + 6m = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 3 \\ x = 2m \\ \end{matrix} ight..

    Phương trình (1) có nghiệm duy nhất \Leftrightarrow \left\lbrack \begin{matrix} 2m = 3 \\ 2m \leq 2 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} m = \frac{3}{2} \\ m \leq 1 \\ \end{matrix} ight..

  • Câu 4: Thông hiểu

    Tìm điểm thỏa mãn

    Miền nghiệm của bất phương trình - 3x + y + 2 \leq 0 không chứa điểm nào sau đây?

    Xét điểm A(1\ \ ;\ \ 2). Ta có: - 3.1 + 2 + 2 = 1 > 0 nên miền nghiệm của bất phương trình trên không chứa điểm A(1\ \ ;\ \ 2).

  • Câu 5: Thông hiểu

    Xét tính đúng sai của các khẳng định

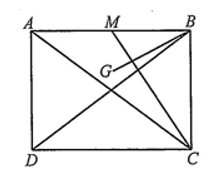
    Cho hình chữ nhật ABCD,AB = 4a,AD = 3a. Gọi M là trung điểm của AB,G là trọng tâm tam giác ACM (Hình vẽ).

    a) \overrightarrow{CM} = \frac{1}{2}\overrightarrow{BA} - 3\overrightarrow{BC}. Sai||Đúng

    b) \overrightarrow{BG} = \frac{3}{2}\overrightarrow{BA} + \frac{1}{3}\overrightarrow{BC}. Sai||Đúng

    c) \overrightarrow{BC}.\overrightarrow{BA} = 0. Đúng||Sai

    b) \overrightarrow{BG}.\overrightarrow{CM} = - a^{2}. Sai||Đúng

    Đáp án là:

    Cho hình chữ nhật ABCD,AB = 4a,AD = 3a. Gọi M là trung điểm của AB,G là trọng tâm tam giác ACM (Hình vẽ).

    a) \overrightarrow{CM} = \frac{1}{2}\overrightarrow{BA} - 3\overrightarrow{BC}. Sai||Đúng

    b) \overrightarrow{BG} = \frac{3}{2}\overrightarrow{BA} + \frac{1}{3}\overrightarrow{BC}. Sai||Đúng

    c) \overrightarrow{BC}.\overrightarrow{BA} = 0. Đúng||Sai

    b) \overrightarrow{BG}.\overrightarrow{CM} = - a^{2}. Sai||Đúng

    a) Sai

    b) Sai

    c) Đúng

    d) Sai

    Ta có: \overrightarrow{CM} = \overrightarrow{BM} - \overrightarrow{BC} = \frac{1}{2}\overrightarrow{BA} - \overrightarrow{BC}.

    Vì G là trọng tâm của tam giác ACM nên

    3\overrightarrow{BG} =\overrightarrow{BA} +\overrightarrow{BM} +\overrightarrow{BC}

    = \overrightarrow{BA} + \frac{1}{2}\overrightarrow{BA} + \overrightarrow{BC} = \frac{3}{2}\overrightarrow{BA} + \overrightarrow{BC}

    \Rightarrow \overrightarrow {BG} = \frac{1}{2}\overrightarrow {BA} + \frac{1}{3}\overrightarrow {BC}

    Vì ABCD là hình chữ nhật nên BC = AD = 3a,\overrightarrow{BC} \cdot \overrightarrow{BA} = 0.

    Ta có: \overrightarrow{BG} \cdot \overrightarrow{CM} = \left( \frac{1}{2}\overrightarrow{BA} + \frac{1}{3}\overrightarrow{BC} \right) \cdot \left( \frac{1}{2}\overrightarrow{BA} - \overrightarrow{BC} \right)

    = \frac{1}{4}{\overrightarrow {BA} ^2} - \frac{1}{3}\overrightarrow {BA} \cdot \overrightarrow {BC} - \frac{1}{3}{\overrightarrow {BC} ^2}

    = \frac{1}{4}(4a)^{2} - \frac{1}{3} \cdot 4a \cdot 3a - \frac{1}{3}(3a)^{2} = - 3a^{2}.

  • Câu 6: Thông hiểu

    Chọn đáp án đúng

    Cho tam giác ABC với A(3;1),\ B(4;2),\ C(4; - 3). Tìm D để ABCD là hình bình hành?

    Ta có: ABCD là hình bình hành \Leftrightarrow \overrightarrow{AB} = \overrightarrow{DC}

    \Leftrightarrow \left\{ \begin{matrix} 4 - 3 = 4 - x_{D} \\ 2 - 1 = - 3 - y_{D} \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x_{D} = - 3 \\ y_{D} = - 4 \end{matrix} \right.\ \Rightarrow D( - 3; - 4).

  • Câu 7: Thông hiểu

    Chọn khẳng định đúng

    Cho hàm số y = f(x) có đồ thị như hình vẽ. Hãy so sánh f(2017) với số 0.

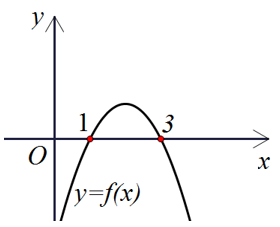
    Nhìn đồ thị, ta thấy đồ thị y = f(x) cắt trục hoành tại 2 điểm x = 1, x = 3 nên Δ > 0, dựa vào hình dạng parabol nên suy ra a < 0 và ta có bảng xét dấu như sau:

    Dựa vào bảng xét dấu thì f(x) < 0 khi x < 1 ∨ x > 3. Mà 2017 > 3 nên f(2017) < 0.

  • Câu 8: Nhận biết

    Tìm trục đối xứng

    Trục đối xứng của parabol y =  − x2 + 5x + 3 là đường thẳng có phương trình

    Trục đối xứng của parabol y = ax2 + bx + c là đường thẳng x = - \frac{b}{2a}.

    Trục đối xứng của parabol y =  − x2 + 5x + 3 là đường thẳng x = \frac{5}{2}.

  • Câu 9: Vận dụng

    Tìm m thỏa mãn điều kiện

    Hỏi có bao nhiêu giá trị m nguyên trong nửa khoảng [ − 10;  − 4) để đường thẳng d : y =  − (m+1)x + m + 2 cắt Parabol (P) : y = x2 + x − 2 tại hai điểm phân biệt cùng phía với trục tung?

    Xét phương trình:  − (m+1)x + m + 2 = x2 + x − 2

     ⇔ x2 + x(m+2) − m − 4 = 0

    Để đường thẳng d cắt Parabol(P) tại hai điểm phân biệt cùng phía với trục tung vậy điều kiện là \left\{ \begin{matrix} \Delta > 0 \\ P > 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} (m + 2)^{2} + 4(m + 4) > 0 \\ - m - 4 > 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} m^{2} + 8m + 20 > 0\ ,\ \forall m \\ m < - 4 \\ \end{matrix} ight.

    Vậy trong nửa khoảng[ − 10;  − 4) có 6 giá trị nguyên m.

  • Câu 10: Nhận biết

    Hoàn thành khẳng định

    Tứ giác MNPQ là hình bình hành nếu:

    Hình vẽ minh họa

    Hoàn thành khẳng định

    Ta có MNPQ là hình bình hành nếu \overrightarrow {MN} = \overrightarrow {QP}

  • Câu 11: Thông hiểu

    Giá trị lượng giác nào sau đây luôn dương?

    Cho \frac{\pi}{2} < \alpha < \pi. Giá trị lượng giác nào sau đây luôn dương?

    Ta có \sin(\pi + \alpha) = - \sin\alpha; \cot\left( \frac{\pi}{2} - \alpha ight) = \sin\alpha; \cos( - \alpha) = \cos\alpha; \tan(\pi + \alpha) = \tan\alpha.

    Do \frac{\pi}{2} < \alpha < \pi ightarrow \left\{ \begin{matrix} \sin\alpha > 0 \\ \cos\alpha < 0 \\ \tan\alpha < 0 \\ \end{matrix} ight..

  • Câu 12: Vận dụng

    Tính độ lớn của vectơ

    Cho hai vectơ \overrightarrow{a}và \overrightarrow{b}. Biết \left| \overrightarrow{a} ight| =2 , \left| \overrightarrow{b} ight|= \sqrt{3} và \left( \overrightarrow{a},\overrightarrow{b} ight) = 120^{o}. Tính\left| \overrightarrow{a} + \overrightarrow{b} ight|.

    Ta có: \left| \overrightarrow{a} + \overrightarrow{b} ight| = \sqrt{\left( \overrightarrow{a} + \overrightarrow{b} ight)^{2}} = \sqrt{{\overrightarrow{a}}^{2} + {\overrightarrow{b}}^{2} + 2\overrightarrow{a}.\overrightarrow{b}} = \sqrt{\left| \overrightarrow{a} ight|^{2} + \left| \overrightarrow{b} ight|^{2} + 2\left| \overrightarrow{a} ight|\left| \overrightarrow{b} ight|\ \ cos\left( \overrightarrow{a},\overrightarrow{b} ight)} = \sqrt{7 - 2\sqrt{3}}.

  • Câu 13: Thông hiểu

    Xác định tổng các vecto

    Tổng \overrightarrow{MN} + \overrightarrow{PQ} + \overrightarrow{RN} + \overrightarrow{NP} + \overrightarrow{QR} bằng vectơ nào sau đây?

    Ta có

    \overrightarrow{MN} + \overrightarrow{PQ} + \overrightarrow{RN} + \overrightarrow{NP} + \overrightarrow{QR}

    = \overrightarrow{MN} + \overrightarrow{NP} + \overrightarrow{PQ} + \overrightarrow{QR} + \overrightarrow{RN}

    = \overrightarrow{MN}.

  • Câu 14: Vận dụng

    Trong các mệnh đề sau mệnh đề nào:

    Trong các mệnh đề sau mệnh đề nào:

    Với n = 3\mathbb{\in N \Rightarrow}n^{2} \vdots 9 nhưng n không chia hết cho 9.

    Chọn đáp án \forall n\mathbb{\in N},n^{2} \vdots 9 \Rightarrow n \vdots 9.

  • Câu 15: Thông hiểu

    Tính diện tích tam giác

    Diện tích tam giác có ba cạnh lần lượt là \sqrt{3},\sqrt{2} và 1 là:

    Nửa chu vi của tam giác là: p = \frac{{a + b + c}}{2} = \frac{{\sqrt 3 + \sqrt 2 + 1}}{2}

    Áp dụng công thức Herong ta có:

    \begin{matrix} S = \sqrt {p\left( {p - a} ight)\left( {p - b} ight)\left( {p - a} ight)} \hfill \\ S = \sqrt {p\left( {p - \sqrt 3 } ight)\left( {p - \sqrt 2 } ight)\left( {p - 1} ight)} \hfill \\ S = \dfrac{{\sqrt 2 }}{2} \hfill \\ \end{matrix}

  • Câu 16: Vận dụng

    Tính bán kính đường tròn ngoại tiếp

    Một tam giác có ba cạnh là 52,56,60. Bán kính đường tròn ngoại tiếp là:

    Ta có: p = \frac{a + b + c}{2} = \frac{52 + 56 + 60}{2} = 84.

    Suy ra: S = \sqrt{p(p - a)(p - b)(p - c)} = \sqrt{84(84 - 52)(84 - 56)(84 - 60)} = 1344.

    Mà S = \frac{abc}{4R} \Rightarrow R = \frac{abc}{4S} = \frac{52.56.60}{4.1344} = \frac{65}{2}.

  • Câu 17: Nhận biết

    Tính độ dài bán kính đường tròn ngoại tiếp

    Cho \Delta ABCcó S = 84,a = 13,b = 14,c = 15. Độ dài bán kính đường tròn ngoại tiếp R của tam giác trên là:

    Ta có: S_{\Delta ABC} = \frac{a.b.c}{4R} \Leftrightarrow R = \frac{a.b.c}{4S} = \frac{13.14.15}{4.84} = \frac{65}{8}.

  • Câu 18: Thông hiểu

    Chọn đáp án đúng

    Cho bốn điểm A,\ B,\ C,\ Dphân biệt. Khi đó vectơ \overrightarrow{u} = \overrightarrow{AD} - \overrightarrow{CD} + \overrightarrow{CB} - \overrightarrow{DB} là:

    Ta có:

    \overrightarrow{u} = \overrightarrow{AD} - \overrightarrow{CD} + \overrightarrow{CB} - \overrightarrow{DB}

    = \overrightarrow{AD} + \overrightarrow{DC} + \overrightarrow{CB} + \overrightarrow{BD} = \overrightarrow{AC} + \overrightarrow{CD} = \overrightarrow{AD}.

  • Câu 19: Thông hiểu

    Tìm công thức Parabol

    Xác định parabol (P) : y = 2x2 + bx + c, biết rằng (P) đi qua điểm M(0;4) và có trục đối xứng x = 1.

    Ta có M \in (P)\overset{}{ightarrow}c = 4.

    Trục đối xứng - \frac{b}{2a} = 1\overset{}{ightarrow}b = - 4.

    Vậy (P) : y = 2x2 − 4x + 4.

  • Câu 20: Nhận biết

    Chọn đẳng thức đúng

    Cho ba điểm phân biệt A,B,C. Đẳng thức nào sau đây là đúng?

    Ta có: \overrightarrow{AB} + \overrightarrow{CA} = \overrightarrow{CA} + \overrightarrow{AB} = \overrightarrow{CB} (Quy tắc 3 điểm).

  • Câu 21: Thông hiểu

    Xác định các tập hợp bằng nhau

    Trong các tập hợp sau, tập hợp nào bằng nhau:

    • A = \left \{ {0; 2; 4; 6; 8} ight \}, B = {x| x ∈ \mathbb{ℕ}, x chia hết cho 2 và x < 12}

    => A = \left \{ {0; 2; 4; 6; 8} ight \}; B = \left \{ {0; 2; 4; 6; 8; 10} ight \}. Vậy tập hợp A không bằng tập hợp B.

    • A = {x| x ∈ \mathbb{ℕ}, x ⋮ 2 và 2< x < 6}, B = {x| x ∈ \mathbb{ℕ}, x chia hết cho 4 và 1 < x < 5}

    => A = \left \{ {4} ight \} ; B = \left \{ {4} ight \}. Vậy tập hợp A bằng tập hợp B. Đáp án đúng

    • A = \left \{ {2; 4; 6; 8} ight \}, B = {x| x ∈ \mathbb{ℕ}, x chia hết cho 2 và x < 10}

    => A = \left \{ {2; 4; 6; 8} ight \}; B =\left \{ {0; 2; 4; 6; 8} ight \}. Vậy tập hợp A không bằng tập hợp B.

    • A = {x| x ∈ \mathbb{ℕ}, x chia hết cho 3 và x < 12}, B = {x| x ∈ \mathbb{ℕ}, x chia hết cho 4 và x < 12}

    => A = \left \{{0; 3; 6; 9} ight \}; B =\left \{ {0; 4; 8} ight \}. Vậy tập hợp A không bằng tập hợp B.

  • Câu 22: Thông hiểu

    Tìm tập nghiệm của bất phương trình

    Tập nghiệm S của bất phương trình 5(x+1)−x(7−x)>−2x là:

     Ta có: 5(x+1)−x(7−x)>−2x \Leftrightarrow x^2+5>0 (hiển nhiên).

    Vậy S = \mathbb{R}.

  • Câu 23: Thông hiểu

    Tìm hệ bất phương trình thỏa mãn đề bài

    Phần tô màu trong hình dưới đây biểu diễn miền nghiệm của hệ bất phương trình nào?

    Tìm hệ bất phương trình thỏa mãn đề bài

    Quan sát hình vẽ ta thấy các giá trị của x thuộc miền nghiệm nhỏ hơn 0

    => Các hệ phương trình \left\{\begin{matrix}x-2y+6\leq 0 \\ 2x-3y\geq 0\\ x\geq 0\end{matrix}ight.; \left\{\begin{matrix}x-2y+6\geq 0 \\ 2x-3y\leq 0\\ x\geq 0\end{matrix}ight. không thỏa mãn.

    Thay tọa độ điểm M(-3;1) vào biểu thức 2x - 3y ta thấy:

    2.\left( { - 2} ight) - 3.\left( 1 ight) = - 7 < 0

    Vậy hệ bất phương trình thỏa mãn hình vẽ đã cho là: \left\{\begin{matrix}x-2y+6\geq 0 \\ 2x-3y\leq 0\\ x\leq 0\end{matrix}ight.

  • Câu 24: Vận dụng

    Tìm x thỏa mãn điều kiện

    Hỏi có bao nhiêu giá trị nguyên của x thỏa mãn bất phương trình \frac{x^{4} - x^{2}}{x^{2} + 5x + 6} \leq 0 ?

    Bất phương trình \frac{x^{4} - x^{2}}{x^{2} + 5x + 6} \leq 0 \Leftrightarrow \frac{x^{2}\left( x^{2} - 1 ight)}{x^{2} + 5x + 6} \leq 0\ \ \ \ \ \ \ \ \ \ \ \ \ (*).

    Vì x2 ≥ 0,  ∀x ∈ ℝ nên bất phương trình

    (*) \Leftrightarrow \left\lbrack \begin{matrix} x^{2} = 0 \\ \frac{x^{2} - 1}{x^{2} + 5x + 6} \leq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ f(x) = \frac{x^{2} - 1}{x^{2} + 5x + 6} \leq 0 \\ \end{matrix} ight.\ .

    Phương trình x^{2} - 1 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - \ 1 \\ \end{matrix} ight. và x^{2} + 5x + 6 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - \ 2 \\ x = - \ 3 \\ \end{matrix} ight.\ .

    Bảng xét dấu

    Dựa vào bảng xét dấu, ta thấy f(x) ≤ 0 ⇔ x ∈ (−3 ; −2) ∪ [ − 1 ; 1].

    Kết hợp với x ∈ ℤ ta được x = {−1 ; 0 ; 1}.

    Vậy có tất cả 3 giá trị nguyên cần tìm.

  • Câu 25: Thông hiểu

    Tìm m thỏa mãn điều kiện

    Tìm m để hệ bất phương trình sau trở thành hệ bất phương trình bậc nhất hai ẩn: \left\{\begin{matrix}mx^{2}+2(m+1)x+y<1\\ my^{2}+3x-4y-1>0\end{matrix}ight..

    Để hệ bất phương trình \left\{\begin{matrix}mx^{2}+2(m+1)x+y<1\\ my^{2}+3x-4y-1>0\end{matrix}ight. trở thành hệ bất phương trình bậc nhất hai ẩn thì hệ số đứng trước x^2,y^2 phải bằng 0 nghĩa là:

    m=0

    Vậy với m=0 thì hệ bất phương trình đã cho trở thành hệ bất phương trình bậc nhất hai ẩn.

  • Câu 26: Nhận biết

    Tìm câu không phải mệnh đề

    Chọn phát biểu không phải là mệnh đề.

    Vì “Hôm nay trời không mưa” là câu không phân biệt được đúng hay sai nên Phương án đó không phải là mệnh đề.

  • Câu 27: Thông hiểu

    Xét tính đúng sai của các khẳng định

    Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A( - 3;0), B(3;0) và C(2;6).

    a) Tích vô hướng của hai véc tơ là một số. Đúng||Sai

    b) \overrightarrow{AB}.\overrightarrow{BC} = 8. Sai||Đúng

    c) AB vuông góc với trục Ox. Đúng||Sai

    d) Gọi H(a;b) là trực tâm của tam giác đã cho. Tính được giá trị biểu thức a - 6b = 2. Sai||Đúng

    Đáp án là:

    Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A( - 3;0), B(3;0) và C(2;6).

    a) Tích vô hướng của hai véc tơ là một số. Đúng||Sai

    b) \overrightarrow{AB}.\overrightarrow{BC} = 8. Sai||Đúng

    c) AB vuông góc với trục Ox. Đúng||Sai

    d) Gọi H(a;b) là trực tâm của tam giác đã cho. Tính được giá trị biểu thức a - 6b = 2. Sai||Đúng

    a) Đúng

    b) Sai

    c) Đúng

    d) Sai

    a) Tích vô hướng của hai vectơ là một số.

    b) Ta có: \overrightarrow{AB} = (6;0);\overrightarrow{BC} = ( - 1;6) \Rightarrow \overrightarrow{AB}.\overrightarrow{BC} = - 6 + 0 = - 6

    c) \overrightarrow{AB} = (6;0);\overrightarrow{i} = (0;1)\ \Rightarrow \ \ \overrightarrow{AB}.\overrightarrow{i} = 0 \Rightarrow \overrightarrow{AB}\bot\overrightarrow{i}.

    Vậy AB vuông góc với trục Ox.

    d) Gọi H(a;b) là trực tâm của tam giác đã cho.

    Ta có:

    \overrightarrow{AH} = (a + 3\ ;\ b)\ ,\ \overrightarrow{BC} = ( - 1\ ;\ 6)\ ,\ \overrightarrow{BH} = (a - 3\ ;\ b)\ ,\ \overrightarrow{AC} = (5\ ;\ 6)

    Vì H là trực tâm tam giác ABCnên:

    \left\{ \begin{matrix} AH\bot BC \\ BH\bot AC \end{matrix} \right. \Leftrightarrow \left\{ \begin{matrix} \overrightarrow{AH}.\overrightarrow{BC} = 0 \\ \overrightarrow{BH}.\overrightarrow{AC} = 0 \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix}- a - 3 + 6b = 0 \\5a - 15 + 6b = 0\end{matrix} \right. \Leftrightarrow \left\{ \begin{matrix} - a + 6b = 3 \\ 5a + 6b = 15 \end{matrix} \right. \Leftrightarrow \left\{ \begin{matrix} a = 2 \\ b = \frac{5}{6} \end{matrix} \right.

    Suy ra a - 6b = - 3.

  • Câu 28: Thông hiểu

    Tìm mệnh đề đúng

    Trong các mệnh đề sau, mệnh đề nào đúng?

    Mệnh đề “\forall x\mathbb{\in R}, (x - 1)^{2} \neq x - 1.” sai vì với x = 1 thì (x - 1)^{2} = x - 1.

    Mệnh đề “\forall x\mathbb{\in R},\ \ |x| < 3 \Leftrightarrow \ \ x < 3” sai vì khi x = - 4 < 3 nhưng |x| = 4 > 3.

    Mệnh đề “\exists n\mathbb{\in N},n^{2} + 1 chia hết cho 4” sai vì

    Nếu n = 2k\ \ \left( k\mathbb{\in N} \right) thì n^{2} + 1 = 4k^{2} + 1 số này không chia hết cho 4.

    Nếu n = 2k + 1\ \ \left( k\mathbb{\in N} \right) thì n^{2} + 1 = 4k^{2} + 4k + 2 số này cũng không chia hết cho 4.

    Mệnh đề “\forall n\mathbb{\in N},\ \ n^{2} + 1 không chia hết cho 3” đúng vì

    Nếu n = 3k\ \ \left( k\mathbb{\in N} \right) thì n^{2} + 1 = 9k^{2} + 1 số này không chia hết cho 3.

    Nếu n = 3k \pm 1\ \ \left( k \in \mathbb{N}^{*} \right)\lim_{x \rightarrow \infty} thì n^{2} + 1 = 9k^{2} \pm 6k + 2 số này không chia hết cho 3.

  • Câu 29: Nhận biết

    Tam thức bậc hai dương khi và chỉ khi

    Tam thức f(x) = x2 − 2x − 3 nhận giá trị dương khi và chỉ khi

    Ta có: f(x) = x^{2} - 2x - 3 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 1 \\ x = 3 \\ \end{matrix} ight.

    Dựa vào bảng xét dấu, chọn đáp án x ∈ (−∞;−1) ∪ (3;+∞).

  • Câu 30: Nhận biết

    Chọn khẳng định đúng

    Cho hình bình hành ABCD. Với mọi điểm M, ta có khẳng định nào sau đây:

     Ta có: \overrightarrow{MB}-\overrightarrow{MA}=\overrightarrow{MC}-\overrightarrow{MD} \Leftrightarrow \overrightarrow {AB}= \overrightarrow {DC} (Đúng).

  • Câu 31: Nhận biết

    Hãy phủ định mệnh đề P

    Cho mệnh đề P:"\forall x\mathbb{\in R},x^{2} - x - 1 < 0". Mệnh đề phủ định của mệnh đề P là

    Đáp án cần tìm là: \overline{P}:"\exists x\mathbb{\in R},x^{2} - x - 1 \geq 0"

  • Câu 32: Vận dụng cao

    Rút gọn biểu thức

    Cho biểu thức B xác định, rút gọn biểu thức

    B = \sqrt{2} - \frac{1}{\sin(x + 2013\pi)}.\sqrt{\frac{1}{1 + \cos x} + \frac{1}{1 - \cos x}} với \pi < x < 2\pi?

    Ta có:

    \sin(x + 2013\pi) = \sin(x + \pi + 2012\pi) = \sin(x + \pi) = - \sin x

    Do đó:

    B = \sqrt{2} - \frac{1}{\sin(x + 2013\pi)}.\sqrt{\frac{1}{1 + \cos x} + \frac{1}{1 - \cos x}}

    B = \sqrt{2} + \frac{1}{\sin x}.\sqrt{\frac{1 - \cos x + 1 + \cos x}{\left( 1 + \cos x ight)\left( 1 - \cos x ight)}}

    B = \sqrt{2} + \dfrac{1}{\sin x}.\sqrt{\dfrac{2}{1 - \cos^{2}x}}

    B = \sqrt{2} + \frac{1}{\sin x}.\sqrt{\dfrac{2}{\sin^{2}x}}

    B = \sqrt{2}\left( 1 + \frac{1}{\sin x.\left| \sin x ight|} ight)

    Vì \pi < x < 2\pi nên \sin x < 0

    \Rightarrow B = \sqrt{2}\left( 1 -\dfrac{1}{\sin^{2}x} ight) = - \sqrt{2}\cot^{2}x

  • Câu 33: Nhận biết

    Xác định bất phương trình bậc nhất hai ẩn

    Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?

    Ta có: 3x - 7y > 19 là bất phương trình bậc nhất hai ẩn.

  • Câu 34: Vận dụng cao

    Tìm m thỏa mãn điều kiện

    Cho hàm số f(x) = ax2 + bx + c có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) + m − 2018 = 0 có duy nhất một nghiệm.

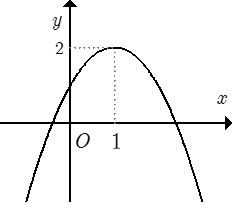
    Phương trình f(x) + m - 2018 = 0\overset{}{\leftrightarrow}f(x) = 2018 - m. Đây là phương trình hoành độ giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = 2018 − m (có phương song song hoặc trùng với trục hoành).

    Dựa vào đồ thị, ta có ycbt 2018 − m = 2 ⇔ m = 2016.

  • Câu 35: Thông hiểu

    Tính giá trị hàm số tại điểm

    Cho hàm số f(x) = \left\{ \begin{matrix} \frac{2\sqrt{x - 2} - 3}{x - 1} & khi & x \geq 2 \\ x^{2} + 2 & khi & x < 2 \\ \end{matrix} ight.. Tính P = f(2) + f(−2).

    Ta có: f(2) + f( - 2) = \frac{2\sqrt{2 - 2} - 3}{2 - 1} + ( - 2)^{2} + 2 \Rightarrow P = 3.

  • Câu 36: Nhận biết

    Tính góc giữa hai vectơ

    Trong mặt phẳng toạ độ Oxy, cho \overrightarrow{OM} = ( - 2;\ - 1), \overrightarrow{ON} = (3;\ - 1). Tính góc \left( \overrightarrow{OM},\ \overrightarrow{ON} \right).

    Ta có:

    \cos\left( \overrightarrow{OM},\ \overrightarrow{ON} \right) = \frac{\overrightarrow{OM}.\overrightarrow{ON}}{OM.ON} = \frac{- 2.3 + ( - 1).( - 1)}{\sqrt{5}.\sqrt{10}} = - \frac{1}{\sqrt{2}}.

    Suy ra \left( \overrightarrow{OM},\ \overrightarrow{ON} \right) = 135^{0}.

  • Câu 37: Nhận biết

    Tìm đẳng thức đúng

    Nếu G là trọng tam giác ABC thì đẳng thức nào sau đây đúng.

    Hình vẽ minh họa

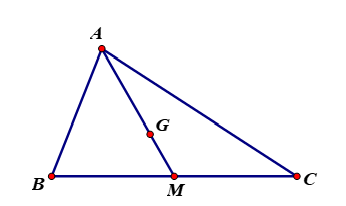
    Gọi M là trung điểm của BC nên ta có

    \overrightarrow{AB}+\overrightarrow{AC} = 2\overrightarrow{AM}

    Mà \overrightarrow{AM} = \frac{3}{2}\overrightarrow{AG} \Rightarrow \overrightarrow{AB} + \overrightarrow{AC} = 2.\frac{3}{2}\overrightarrow{AG} = 3\overrightarrow{AG}

    \Rightarrow \overrightarrow{AG} = \frac{\overrightarrow{AB} + \overrightarrow{AC}}{3}.

  • Câu 38: Nhận biết

    Mệnh đề nào sau đây là đúng?

    Mệnh đề nào sau đây là đúng?

    x = 3 \in (2;3brack nhưng x = 3 otin (2;3) \Rightarrow A sai.

    x = 2 \in \lbrack 2;3brack nhưng x = 2 otin (2;3brack \Rightarrow C sai.

    x = 3 \in \lbrack 2;3brack nhưng x = 3 otin \lbrack 2;3) \Rightarrow D sai.

  • Câu 39: Vận dụng

    Khẳng định nào sau đây là đúng?

    Cho tam giác ABC với trực tâm H. D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây là đúng?

    Ta có BD là đường kính\Rightarrow \overrightarrow{OB} = \overrightarrow{DO}.

    Ta có AH\bot BC,DC\bot BC \Rightarrow AH//DC(1)

    Ta lại cóCH\bot AB,DA\bot AB \Rightarrow CH//DA(2)

    Từ (1)(2) \Rightarrowtứ giác HADC là hình bình hành\Rightarrow \overrightarrow{HA} = \overrightarrow{CD};\overrightarrow{AD} = \overrightarrow{HC}.

  • Câu 40: Nhận biết

    Chọn đáp án chính xác

    Giá trị của \cos60^{0} +\sin30^{0} bằng bao nhiêu?

    Ta có: cos60^{0} + sin30^{0} = \frac{1}{2} + \frac{1}{2} = 1.

  • Câu 41: Vận dụng

    Khẳng định nào sau đây đúng?

    Trong hệ tọa độ Oxy, cho hình bình hành OABC, điểm C thuộc trục hoành. Khẳng định nào sau đây đúng?

    Từ giả thiết suy ra cạnh OC thuộc trục hoành \overset{}{ightarrow} cạnh AB song song với trục hoành nên y_{A} = y_{B}\overset{}{ightarrow}\overrightarrow{AB} = \left( x_{A} - x_{B};0 ight). Do đó loại đáp án \overrightarrow{AB} có tung độ khác 0 và đáp án hai điểm A,\ B có tung độ khác nhau.

    Nếu C có hoành độ bằng 0\overset{}{ightarrow}C(0;0) \equiv O: mâu thuẩn với giả thiết OABC là hình bình hành. Loại đáp án C có hoành độ bằng 0.

    Dùng phương pháp loại trừ, ta chọn x_{A} + x_{C} - x_{B} = 0.

    Cách 2. Gọi I là tâm của hình bình hành OABC. Suy ra

    \bullet I là trung điểm AC\overset{}{ightarrow}I\left( \frac{x_{A} + x_{C}}{2};\frac{y_{A} + 0}{2} ight).

    \bullet I là trung điểm OB\overset{}{ightarrow}I\left( \frac{0 + x_{B}}{2};\frac{0 + y_{B}}{2} ight).

    Từ đó suy ra \frac{x_{A} + x_{C}}{2} =\frac{0 + x_{B}}{2}\overset{}{ightarrow}x_{A} + x_{C} - x_{B} =0.

  • Câu 42: Thông hiểu

    Tìm tập nghiệm của phương trình

    Tập nghiệm của phương trình x + \sqrt{x - 1} = 2 + \sqrt{x - 1}là:

    Phương trình x + \sqrt{x - 1} = 2 +\sqrt{x - 1} \Leftrightarrow \left\{ \begin{matrix}x \geq 1 \\x = 2 \\\end{matrix} ight.\ \Leftrightarrow x = 2.

    Vậy S = {2}.

  • Câu 43: Vận dụng cao

    Tìm giá trị m thỏa mãn điều kiện

    Cho A = \left\{x\in\mathbb{ R}||mx - 3| = mx - 3 ight\}, B = \left\{ x\in\mathbb{ R}|x^{2} - 4 = 0ight\}. Tìm m để B\backslash A = B.

    Ta có:

    |mx - 3| = mx - 3

    \Leftrightarrow mx - 3 \geq 0

    \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {m > 0,x \geqslant \dfrac{3}{m}} \\ {m < 0,x \leqslant \dfrac{3}{m}} \end{array}} ight.

    Do đó m < 0 thì A = \left( - \infty;\frac{3}{m} ightbrack; nếu m > 0 thì A = \left\lbrack \frac{3}{m}; + \infty ight)

    Ta có:x^{2} - 4 = 0 \Leftrightarrow m = \pm 2\mathbb{\in R}

    Do đó B = \left\{ - 2;2 ight\}

    Ta có: B\backslash A = B \Leftrightarrow \left\lbrack \begin{matrix} A eq \varnothing(*) \\ \left\{ \begin{matrix} - 2 otin A \\ 2 otin A \\ \end{matrix}(**) ight.\ \\ \end{matrix} ight.

    TH1: (*) \Leftrightarrow M = 0

    TH2: Nếu m < 0 thì \left( {**} ight) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} { - 2 > \dfrac{3}{m}} \\ {2 > \dfrac{3}{m}} \end{array}} ight.

    \Leftrightarrow - 2 > \frac{3}{m} \Leftrightarrow m > - \frac{3}{2}

    Tóm lại - \frac{3}{2} < m < 0 thì thỏa mãn yêu cầu bài toán.

    TH3: Nếu m > 0 thì \left( {**} ight) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} { - 2 < \dfrac{3}{m}} \\ {2 > \dfrac{3}{m}} \end{array}} ight. \Rightarrow 2 < \dfrac{3}{m} \Rightarrow m < \frac{3}{2}

    Kết hợp ba trường hợp, vậy - \frac{3}{2} < m < \frac{3}{2} thì thỏa mãn yêu cầu bài toán.

  • Câu 44: Nhận biết

    Chọn đáp án đúng

    Trong các vecto dưới đây, vecto nào cùng phương với vecto \overrightarrow{u} = (3; - 2)?

    Nhận thấy \frac{3}{- 9} = \frac{- 2}{6} nên \overrightarrow{d} = ( - 9;6) cùng phương với \overrightarrow{u} = (3; - 2).

  • Câu 45: Thông hiểu

    Chọn đáp án đúng

    Tam giác với ba cạnh là 6;8;10 có bán kính đường tròn ngoại tiếp bằng bao nhiêu?

    Ta có: 6^{2} + 8^{2} = 10^{2} \Rightarrow R = \frac{10}{2} = 5. (Tam giác vuông bán kính đường tròn ngoại tiếp bằng \frac{1}{2} cạnh huyền).

Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 1 Toán 10 Chân trời sáng tạo Đề 3 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
  • Điểm thưởng: 0
Xem đáp án Làm lại
1
15 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Đề thi học kì 1 Toán 10 Chân trời sáng tạo Đề 3
Thời gian còn lại 90:00 Số câu đã làm 0/45
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
Chưa làm Đã làm
Làm lại Nộp bài
Tìm bài trong mục này
🖼️

Toán 10 - Chân trời sáng tạo
Xem thêm