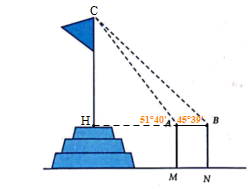
Tính chiều cao ngọn tháp
Giả sử ![]() là chiều cao của tháp trong đó
là chiều cao của tháp trong đó ![]() là chân tháp. Chọn hai điểm
là chân tháp. Chọn hai điểm ![]() trên mặt đất sao cho ba điểm
trên mặt đất sao cho ba điểm ![]() và
và ![]() thẳng hàng. Ta đo được
thẳng hàng. Ta đo được ![]() ,
, ![]() .
.

Chiều cao ![]() của tháp gần với giá trị nào sau đây?
của tháp gần với giá trị nào sau đây?
Áp dụng định lí sin vào tam giác ta có:
Ta có nên
Do đó .
Trong tam giác vuông có