Hàm số và đồ thị sách CTST
Định nghĩa
Giả sử 
\(x\) và \(y\) là hai đại lượng biến thiên, \(x \in D\)
Nếu với mỗi \(x \in D\), ta xác định được y duy nhất (\(y \in \mathbb{R}\)) thì ta có một hàm số.
- \(x\) là biến số, \(y\) là hàm số của \(x\)
- \(D\) là tập xác định
- \(T = \left\{ {y|x \in D} \right\}\) là tập giá trị của hàm số.
- Ta thường kí hiệu \(f(x)\) là giá trị \(y\) tương ứng với \(x\), nên hàm số thường viết là \(y = f(x)\)
|
Chú ý
|
Ví dụ: Tìm tập xác định của các hàm số sau:
| a) \(y = x - \frac{2}{{x - 3}}\) |
b) \(y = x + \sqrt {x + 1}\) |
Hướng dẫn giải
a) Điều kiện để hàm số có nghĩa là: \(x - 3 \ne 0\) có nghĩa là \(x \ne 3\)
Vậy tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ 3 \right\}\)
b) Điều kiện để hàm số có nghĩa là: \(x + 1 \geqslant 0\) có nghĩa là \(x \geqslant - 1\)
Vậy tập xác định của hàm số là
2. Đồ thị hàm số
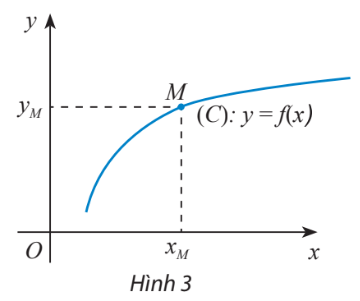
Cho hàm số \(y = f(x)\) xác định trên \(D\), Khi đó đồ thị \((C) = \left\{ {M(x;f(x))|x \in D} \right\}\)
Điểm \(M({x_M};{y_M})\) thuộc đồ thị hàm số \(y = f(x) \Leftrightarrow \left\{ \begin{array}{l}{x_M} \in D\\{y_M} = f({x_M})\end{array} \right.\)
Ví dụ: Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}
{3x - 2{\text{ khi }}x \leqslant 0} \\
{1 - 2{x^2}{\text{ khi }}x < 1}
\end{array}} \right.\). Tính giá trị của \(f\left( 1 \right);f\left( 2 \right);f\left( 0 \right);f\left( { - 3} \right)\).
Hướng dẫn giải
Ta có:
\(\begin{matrix}
f\left( 1 \right) = 3.1 - 2 = 1 \hfill \\
f\left( 2 \right) = 3.2 - 2 = 4 \hfill \\
f\left( 0 \right) = 1 - {2.0^2} = 1 \hfill \\
f\left( { - 3} \right) = 1 - 2.{\left( { - 3} \right)^2} = - 17 \hfill \\
\end{matrix}\)
3. Hàm số đồng biến, hàm số nghịch biến
Định nghĩa
Cho hàm số \(y = f(x)\) xác định trên khoảng \((a;b)\)
- Hàm số đồng biến trên khoảng \((a;b)\) nếu:
\(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\)
\(\Leftrightarrow \forall {x_1},{x_2} \in \left( {a;b} \right):{x_1} \ne {x_2} \Rightarrow \frac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{{x_1} - {x_2}}} > 0\)
- Hàm số nghịch biến trên khoảng \((a;b)\) nếu:
\(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\)
\(\Leftrightarrow \forall {x_1},{x_2} \in \left( {a;b} \right):{x_1} \ne {x_2} \Rightarrow \frac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{{x_1} - {x_2}}} < 0\)
Quan sát đồ thị: trên khoảng \((a;b)\)
- Hàm số đồng biến (tăng) thì đồ thị có dạng đi lên từ trái sang phải.
- Hàm số nghịch biến (giảm) thì đồ thị có dạng đi xuồng từ trái sang phải.
Ví dụ: Dùng định nghĩa để chứng minh sự đồng biến và nghịch biến của các hàm số:
| a) \(y = 2x + 3\) |
b) \(y = \frac{4}{{x + 1}}\) trên \(\left( { - 1; + \infty } \right)\) |
Hướng dẫn giải
a) Tập xác định: \(D = \mathbb{R}\)
Gọi \({x_1};{x_2}\) là hai giá trị phân biệt tùy ý thuộc \(\mathbb{R}\) ta có:
\(\begin{matrix}
\dfrac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{{x_1} - {x_2}}} \hfill \\
= \dfrac{{\left( {2{x_1} + 3} \right) - \left( {2{x_2} + 3} \right)}}{{{x_1} - {x_2}}} \hfill \\
= \dfrac{{2\left( {{x_1} - {x_2}} \right)}}{{{x_1} - {x_2}}} = 2 > 0 \hfill \\
\end{matrix}\)
Vậy hàm số \(y = 2x + 3\) đồng biến trên \(\mathbb{R}\).
b) Gọi \({x_1};{x_2}\) là hai giá trị phân biệt tùy ý thuộc \(\left( { - 1; + \infty } \right)\) ta có:
\(\begin{matrix}
\dfrac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{{x_1} - {x_2}}} = \dfrac{{\dfrac{4}{{{x_1} + 1}} - \dfrac{4}{{{x_2} + 1}}}}{{{x_1} - {x_2}}} \hfill \\
= \dfrac{{\dfrac{{4\left( {{x_1} - {x_2}} \right)}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}}}{{{x_1} - {x_2}}} = \dfrac{{ - 4}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}} \hfill \\
\end{matrix}\)
Do \({x_1} > - 1,{x_2} > - 1\) nên \(\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) > 0\) từ đó ta có: \(\frac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{{x_1} - {x_2}}} < 0\)
Vậy hàm số \(y = \frac{4}{{x + 1}}\) nghịch biến trên \(\left( { - 1; + \infty } \right)\).
