Bất phương trình bậc nhất hai ẩn sách CTST
Bất phương trình bậc nhất hai ẩn 
\(x, y\) là bất phương trình có một trong các dạng
\(\begin{matrix}
ax + by + c \leqslant 0 \hfill \\
ax + by + c \geqslant 0 \hfill \\
ax + by + c < 0 \hfill \\
ax + by + c > 0 \hfill \\
\end{matrix}\)
trong đó \(a, b, c\) là những số cho trước, \(a\) và \(b\) không đồng thời bằng \(0\), \(x\) và \(y\) là các ẩn.
Ví dụ: \(2x + 3y - 10 > 0\)
2. Nghiệm của bất phương trình bậc nhất hai ẩn
Mỗi cặp số \(({x_0};{y_0})\) thỏa mãn \(a{x_0} + b{y_0} + c\; < 0\) được gọi là một nghiệm của bất phương trình đã cho.
Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.
Ví dụ: Cặp số \((3;5)\) là một nghiệm của bất phương trình \(2x + 3y - 10 > 0\) vì \(2.3 + 3.5 - 10 = 11 > 0\)
3. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn
Trong mặt phẳng tọa độ \(Oxy\), tập hợp các điểm \(({x_0};{y_0})\) sao cho \(a{x_0} + b{y_0} + c < 0\) được gọi là miền nghiệm của bất phương trình \(ax + by + c < 0\).
Biểu diễn miền nghiệm của bất phương trình \(ax + by + c < 0\)
Bước 1: Trên mặt phẳng \(Oxy\), vẽ đường thẳng \(\Delta :ax + by + c = 0.\)
Bước 2: Lấy một điểm \(M({x_0};{y_0})\) không thuộc \(\Delta\). Tính \(a{x_0} + b{y_0} + c\)
Bước 3: Kết luận
- Nếu \(a{x_0} + b{y_0} + c < 0\) thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ \(\Delta\)) chứa điểm \(M\).
- Nếu \(a{x_0} + b{y_0} + c > 0\) thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ \(\Delta\)) không chứa điểm \(M\).
Chú ý
Nếu \(c \ne 0\) ta thường chọn \(M\) là gốc tọa độ.
Nếu \(c = 0\) ta thường chọn \(M\) có tọa độ \((1;0)\) hoặc \((0;1)\).
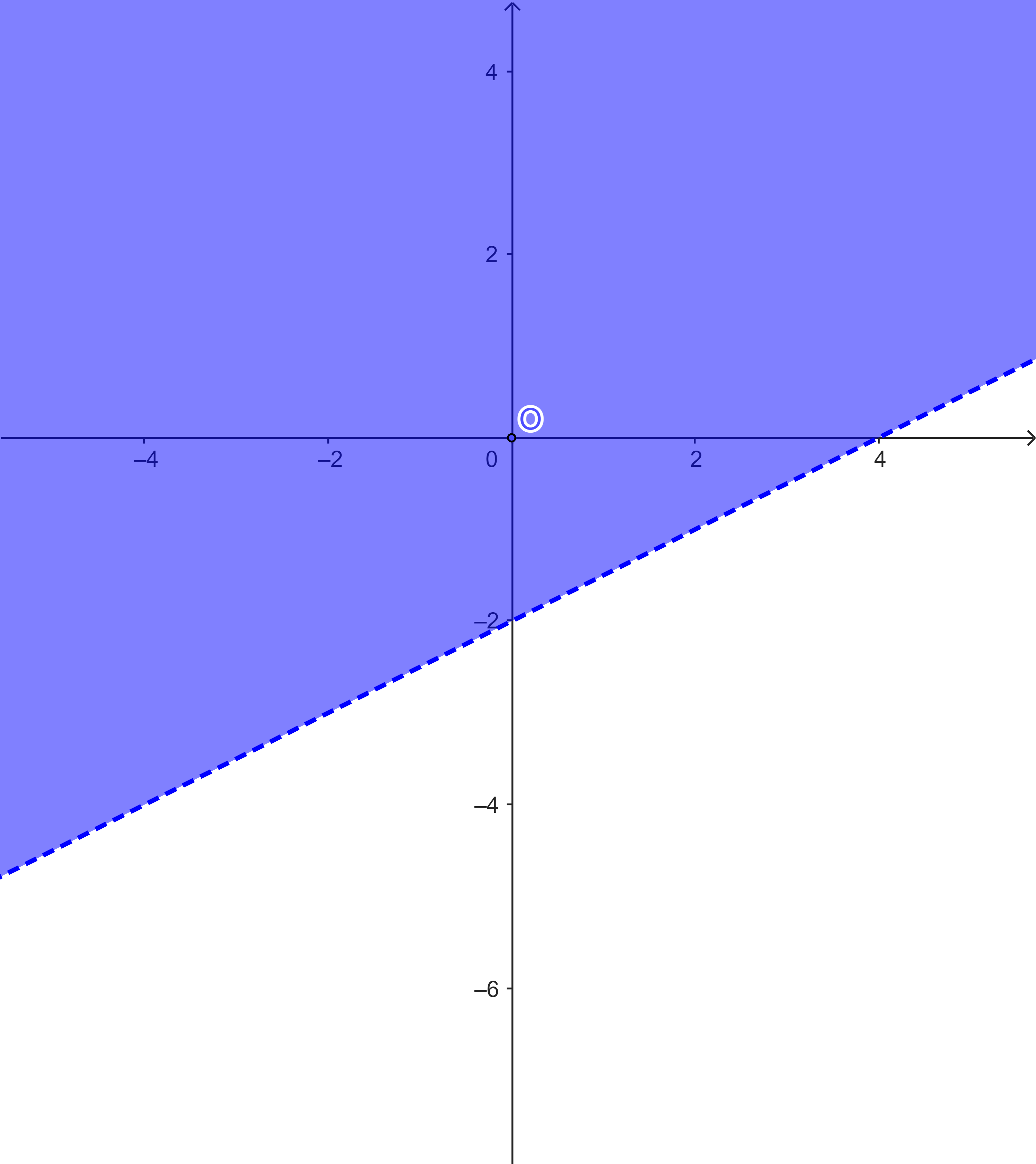
Ví dụ: Biểu diễn hình học tập nghiệm của bất phương trình bậc nhất hai ẩn \(2x−4y < 8\).
Hướng dẫn giải
Vẽ đường thẳng \(d : 2x−4y = 8\).
Thay tọa độ điểm \(O(0; 0)\) vào vế trái phương trình đường thẳng \((d)\), ta được: \(0 < 8\).
Vậy miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm \(O\). (Trên hình là nửa mặt phẳng tô màu).
