Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 10 Khóa học Lớp 10 Toán 10 - Chân trời sáng tạo
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Đề kiểm tra 45 phút Chương 5 Vectơ Sách CTST

Mô tả thêm:

Đề kiểm tra 45 phút Toán 10 Chương 5 Vectơ sách Chân trời sáng tạo giúp bạn học tổng hợp lại kiến thức của cả nội dung chương. Cùng nhau luyện tập nha!
  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Bắt đầu làm bài
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
  • Câu 1: Nhận biết

    Điều kiện cần và đủ để ba điểm thẳng hàng

    Cho ba điểm A,\ B,\ C phân biệt. Điều kiện cần và đủ để ba điểm đó thẳng hàng là

    Ta có tính chất: Điều kiện cần và đủ để ba điểm A,\ B,\ C phân biệt thẳng hàng là \exists k \in R:\overrightarrow{AB} = k\overrightarrow{AC}.

  • Câu 2: Nhận biết

    Chọn khẳng định đúng

    Cho ba vectơ \overrightarrow{a},\ \ \ \overrightarrow{b}\ và\ \overrightarrow{c} đều khác vectơ – không. Trong đó hai vectơ \overrightarrow{a},\ \ \ \overrightarrow{b} cùng hướng, hai vectơ \overrightarrow{a}\ ,\ \overrightarrow{c}đối nhau. Khẳng định nào sau đây đúng?

    Hình vẽ minh họa

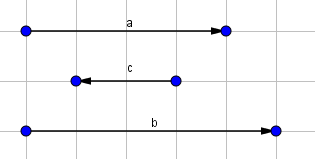
    Khẳng định đúng là: “Hai vectơ \ \ \overrightarrow{b}\ \ \ và\ \overrightarrow{c} ngược hướng”.

  • Câu 3: Thông hiểu

    Xác định đẳng thức sai

    Gọi O là tâm hình bình hành ABCD. Đẳng thức nào sau đây sai?

    Hình vẽ minh họa

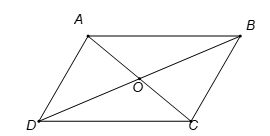
    Xét các đáp án:

    • Đáp án \overrightarrow{OA} - \overrightarrow{OB} = \overrightarrow{CD}.. Ta có \overrightarrow{OA} - \overrightarrow{OB} = \overrightarrow{BA} = \overrightarrow{CD}. Vậy \overrightarrow{OA} - \overrightarrow{OB} = \overrightarrow{CD}. đúng.

    • Đáp án \overrightarrow{OB} - \overrightarrow{OC} = \overrightarrow{OD} - \overrightarrow{OA}. Ta có \left\{ \begin{matrix} \overrightarrow{OB} - \overrightarrow{OC} = \overrightarrow{CB} = - \overrightarrow{AD} \\ \overrightarrow{OD} - \overrightarrow{OA} = \overrightarrow{AD} \end{matrix} \right.. Vậy \overrightarrow{OB} - \overrightarrow{OC} = \overrightarrow{OD} - \overrightarrow{OA}. sai.

    • Đáp án \overrightarrow{AB} - \overrightarrow{AD} = \overrightarrow{DB}. Ta có \overrightarrow{AB} - \overrightarrow{AD} = \overrightarrow{DB}. Vậy \overrightarrow{AB} - \overrightarrow{AD} = \overrightarrow{DB}. đúng.

    • Đáp án \overrightarrow{BC} - \overrightarrow{BA} = \overrightarrow{DC} - \overrightarrow{DA}. Ta có \left\{ \begin{matrix} \overrightarrow{BC} - \overrightarrow{BA} = \overrightarrow{AC} \\ \overrightarrow{DC} - \overrightarrow{DA} = \overrightarrow{AC} \end{matrix} \right.. Vậy \overrightarrow{BC} - \overrightarrow{BA} = \overrightarrow{DC} - \overrightarrow{DA}. đúng.

  • Câu 4: Nhận biết

    Tìm câu sai

    Chọn phát biểu sai?

    Ta có ba điểm phân biệt A,\ B,\ C thẳng hàng khi và chỉ khi \exists\ k\mathbb{\in R},k \neq 0 sao cho \overrightarrow{AB}\ = \ k\overrightarrow{AC}.

  • Câu 5: Nhận biết

    Chọn câu đúng

    Cho tam giác ABC có đường cao BH (H ở trên cạnh AC). Câu nào sau đây đúng?

    Ta có:

    \overrightarrow{BA}.\overrightarrow{CA} = \left( \overrightarrow{BH} + \overrightarrow{HA} \right).\overrightarrow{CA}

    = \overrightarrow{BH}.\overrightarrow{CA} + \overrightarrow{HA}.\overrightarrow{CA} = \overrightarrow{HA}.\overrightarrow{CA} = AH.AC nên chọn \overrightarrow{BA}.\overrightarrow{CA} = AH.AC.

    = \overrightarrow{BH}.\overrightarrow{CA} + \overrightarrow{HA}.\overrightarrow{CA} = \overrightarrow{HA}.\overrightarrow{CA} = AH.AC

  • Câu 6: Nhận biết

    Xác định đẳng thức đúng

    Chọn đẳng thức đúng:

    Đẳng thức đúng là: \overrightarrow{AB} =\overrightarrow{CB}+ \overrightarrow{AC}.

  • Câu 7: Thông hiểu

    Tìm tọa độ vectơ thoả mãn

    Trong hệ tọa độ Oxy, cho tam giác ABC có \ B(9;7),\ C(11; - 1). Gọi M,N lần lượt là trung điểm của AB,\ AC. Tìm tọa độ vectơ \overrightarrow{MN}?

    Ta có \overrightarrow{MN} = \frac{1}{2}\overrightarrow{BC} = \frac{1}{2}(2; - 8) = (1; - 4).

  • Câu 8: Nhận biết

    Tính tích vô hướng

    Cho tam giác đều ABC có cạnh a. Tính tích vô hướng \overrightarrow{AB}\times \overrightarrow{AC}.

     Ta có: \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos A = a.a.\cos 60^\circ = \frac{{{a^2}}}{2}.

  • Câu 9: Thông hiểu

    Xác định cặp vectơ thỏa mãn yêu cầu

    Cặp vectơ nào sau đây vuông góc?

    Phương án \overrightarrow{a} = (2; - 1) và \overrightarrow{b} = ( - 3;4):

    \overrightarrow{a}.\overrightarrow{b} = 2.( - 3) + ( - 1).4 = - 10 \neq 0 suy ra đáp án này sai.

    Phương án \overrightarrow{a} = (3; - 4) và \overrightarrow{b} = ( - 3;4):

    \overrightarrow{a}.\overrightarrow{b} = 3.( - 3) + ( - 4).4 \neq 0 suy ra đáp án này sai.

    Phương án \overrightarrow{a} = ( - 2; - 3) và \overrightarrow{b} = ( - 6;4):

    \overrightarrow{a}.\overrightarrow{b} = - 2.( - 6) - 3.4 = 0 \Rightarrow \overrightarrow{a}\bot\overrightarrow{b} suy ra đáp án này đúng.

    Phương án \overrightarrow{a} = (7; - 3) và \overrightarrow{b} = (3; - 7):

    \overrightarrow{a}.\overrightarrow{b} = 7.3 + ( - 3).( - 7) = 42 \neq 0 suy ra đáp án này sai.

  • Câu 10: Nhận biết

    Điều kiện cần và đủ để ba điểm thẳng hàng.

    Cho ba điểm A,\ B,\ C phân biệt. Điều kiện cần và đủ để ba điểm đó thẳng hàng là

    Ta có tính chất: Điều kiện cần và đủ để ba điểm A,\ B,\ C phân biệt thẳng hàng là \exists k \in R:\overrightarrow{AB} = k\overrightarrow{AC}.

  • Câu 11: Thông hiểu

    Tìm cặp vectơ cùng phương

    Cho tam giác ABC và đặt \overrightarrow{a} = \overrightarrow{BC},\ \ \overrightarrow{b} = \overrightarrow{AC}. Cặp vectơ nào sau đây cùng phương ?

    Dễ thấy - 10\ \overrightarrow{a} - 2\overrightarrow{b} = - \ 2\ \left( 5\overrightarrow{a} + \overrightarrow{b} \right) nên hai vectơ 5\overrightarrow{a} + \overrightarrow{b},\ \ - 10\overrightarrow{a} - 2\overrightarrow{b} cùng phương.

  • Câu 12: Thông hiểu

    Xét tính đúng sai của các khẳng định

    Cho tam giác ABC có M,N lần lượt là trung điểm của AC,BC; AB = a. Các khẳng định sau đúng hay sai?

    a) MN là đường trung bình của tam giác ABC nên MN = \frac{1}{2}AB. Đúng||Sai

    b) \overrightarrow{NB} = \overrightarrow{CN}. Đúng||Sai

    c) \overrightarrow{CM} - \overrightarrow{CN} = \overrightarrow{MN}. Đúng||Sai

    d) \left| \overrightarrow{CM} - \overrightarrow{NB} \right| = \frac{a}{2}. Sai||Đúng

    Đáp án là:

    Cho tam giác ABC có M,N lần lượt là trung điểm của AC,BC; AB = a. Các khẳng định sau đúng hay sai?

    a) MN là đường trung bình của tam giác ABC nên MN = \frac{1}{2}AB. Đúng||Sai

    b) \overrightarrow{NB} = \overrightarrow{CN}. Đúng||Sai

    c) \overrightarrow{CM} - \overrightarrow{CN} = \overrightarrow{MN}. Đúng||Sai

    d) \left| \overrightarrow{CM} - \overrightarrow{NB} \right| = \frac{a}{2}. Sai||Đúng

    a) Đúng

    Ta có: MN là đường trung bình của tam giác ABC nên MN = \frac{1}{2}AB.

    b) Đúng

    Vì N là trung điểm của BC nên \overrightarrow{NB} = \overrightarrow{CN}

    c) Sai

    Ta có: \overrightarrow{CM} - \overrightarrow{CN} = \overrightarrow{NM}

    d) Đúng

    Ta có: \left| \overrightarrow{CM} - \overrightarrow{NB} \right| = \left| \overrightarrow{CM} - \overrightarrow{CN} \right| = \left| \overrightarrow{NM} \right| = \frac{AB}{2} = \frac{a}{2}.

  • Câu 13: Thông hiểu

    Chọn mệnh đề đúng

    Cho ABC là tam giác đều. Mệnh đề nào sau đây đúng?

    Phương án \overrightarrow{AB}.\overrightarrow{AC} = 0: Do\overrightarrow{AB}.\overrightarrow{AC} =AB.AC.\cos60^{o} \neq 0 nên loại.

    Phương án \overrightarrow{AB}.\overrightarrow{AC} = - \overrightarrow{AC}.\overrightarrow{AB}: \left. \ \begin{matrix}\overrightarrow{AB}.\overrightarrow{AC} > 0 \\- \overrightarrow{AC}.\overrightarrow{AB} < 0\end{matrix} \right\}\Rightarrow\overrightarrow{AB}.\overrightarrow{AC} \neq -\overrightarrow{AC}.\overrightarrow{AB} nên loại.

    Phương án \left( \overrightarrow{AB}.\overrightarrow{AC} \right)\overrightarrow{BC} = \overrightarrow{AB}\left( \overrightarrow{AC}.\overrightarrow{BC} \right): Do\left( \overrightarrow{AB}.\overrightarrow{AC} \right)\overrightarrow{BC} và \overrightarrow{AB}\left( \overrightarrow{AC}.\overrightarrow{BC} \right) không cùng phương nên loại.

    Phương án \overrightarrow{AB}.\overrightarrow{AC} = \overrightarrow{BA}.\overrightarrow{BC}: AB = AC = BC = a, \overrightarrow{AB}.\overrightarrow{AC} = \overrightarrow{BA}.\overrightarrow{BC} = \frac{a^{2}}{2} nên chọn.

  • Câu 14: Thông hiểu

    Chọn khẳng định đúng

    Gọi C là trung điểm của đoạn AB. Hãy chọn khẳng định đúng trong các khẳng định sau:

    Ta có C là trung điểm của đoạn \overrightarrow{AB} và \overrightarrow{AC} cùng hướng.

  • Câu 15: Vận dụng

    Chọn khẳng định đúng

    Cho tam giác ABC có điểm O thỏa mãn |\overrightarrow{OA}+\overrightarrow{OB}-2\overrightarrow{OC}|=|\overrightarrow{OA}-\overrightarrow{OB}|. Khẳng định nào sau đây là đúng?

     Ta có: |\overrightarrow{OA}+\overrightarrow{OB}-2\overrightarrow{OC}|=|\overrightarrow{OA}-\overrightarrow{OB}| \Leftrightarrow\left| {\overrightarrow {CA} + \overrightarrow {CB} } ight| = \left| {\overrightarrow {BA} } ight|.

    Vẽ hình bình hành ACBD, suy ra \left| {\overrightarrow {CA} + \overrightarrow {CB} } ight| = \left| {\overrightarrow {CD} } ight|. Mà \left| {\overrightarrow {CA} + \overrightarrow {CB} } ight| = \left| {\overrightarrow {BA} } ight|. Suy ra CD=BA. Do đó ACBD là hình chữ nhật. Do đó tam giác ACB vuông C.

  • Câu 16: Thông hiểu

    Xác định tọa độ điểm B thỏa mãn yêu cầu

    Cho M(2;0),\ N(2;2),\ P( - 1;3) lần lượt là trung điểm các cạnh BC,\ CA,\ AB của \Delta ABC. Tọa độ B là:

    Hình vẽ minh họa:

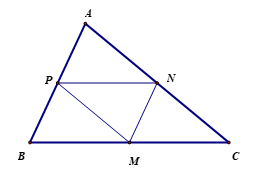
    Ta có: BPNM là hình bình hành nên \left\{ \begin{matrix} x_{B} + x_{N} = x_{P} + x_{M} \\ y_{B} + y_{N} = y_{P} + y_{M} \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix} x_{B} + 2 = 2 + ( - 1) \\ y_{B} + 2 = 0 + 3 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x_{B} = - 1 \\ y_{B} = 1 \end{matrix} \right..

  • Câu 17: Nhận biết

    Tìm câu sai

    Cho ba điểm A,\ B,\ C phân biệt. Đẳng thức nào sau đây là đẳng thức sai?

    Ta có: \overrightarrow{CA} + \overrightarrow{AB} = \overrightarrow{CB} \neq \overrightarrow{BC}.

  • Câu 18: Thông hiểu

    Chọn kết luận đúng

    Cho hình thoi ABCD tâm O, cạnh bằng a và \widehat{A}=60^0. Kết luận nào sau đây là đúng?

    Hình vẽ minh họa

    Chọn kết luận đúng

    Ta có:  ABCD là hình thoi \widehat{A}=60^0

    => \widehat{ADC}=120^0

    Áp dụng định lí cosin trong tam giác ADC ta có:

    \begin{matrix} A{C^2} = A{D^2} + D{C^2} - 2AD.DC\cos {120^0} \hfill \\ \Rightarrow A{C^2} = {a^2} + {a^2} - 2.a.a.\left( { - \dfrac{1}{2}} ight) \hfill \\ \Rightarrow A{C^2} = 3{a^2} \hfill \\ \Rightarrow AC = a\sqrt 3 \hfill \\ \Rightarrow OA = \dfrac{1}{2}AC = \dfrac{{a\sqrt 3 }}{2} \hfill \\ \end{matrix}

    =>AO=|\overrightarrow{AO}|=\frac{a\sqrt{3}}{2}

  • Câu 19: Vận dụng cao

    Xác định k để ba điểm thẳng hàng

    Cho tam giác ABC. Lấy các điểm M,N sao cho \overrightarrow{MA} + \overrightarrow{MB} = \overrightarrow{0};2\overrightarrow{NA} + 3\overrightarrow{NC} = \overrightarrow{0} và \overrightarrow{BC} = k\overrightarrow{BP}. Xác định k để ba điểm M,N,P thẳng hàng.

    Ta có:

    \overrightarrow{MN} = \overrightarrow{AN} - \overrightarrow{AM} = \frac{3}{5}\overrightarrow{AC} - \frac{1}{2}\overrightarrow{AB}

    \overrightarrow{NP} = \overrightarrow{NC} + \overrightarrow{CP}

    = \frac{2}{5}\overrightarrow{AC} - \left( \overrightarrow{BP} - \overrightarrow{BC} ight)

    = \frac{2}{5}\overrightarrow{AC} + \left( \frac{1}{k} - 1 ight)\overrightarrow{BC}

    = \frac{2}{5}\overrightarrow{AC} + \left( \frac{1}{k} - 1 ight)\left( \overrightarrow{AC} - \overrightarrow{AB} ight)

    = \left( \frac{1}{k} - \frac{2}{5} ight)\overrightarrow{AC} + \left( \frac{1}{k} - 1 ight)\overrightarrow{AB}

    Để ba điểm M,N,Pthẳng hàng thì \exists m\mathbb{\in R}:\overrightarrow{NP} = m\overrightarrow{MN} hay

    \left( \frac{1}{k} - \frac{2}{5} ight)\overrightarrow{AC} + \left( \frac{1}{k} - 1 ight)\overrightarrow{AB} = \frac{3m}{5}\overrightarrow{AC} - \frac{m}{2}\overrightarrow{AB}

    \left\{ \begin{matrix}\dfrac{1}{k} - \dfrac{2}{5} = \dfrac{3m}{5} \\\dfrac{1}{k} - 1 = - \dfrac{m}{2} \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}m = 4 \\k = \dfrac{1}{3} \\\end{matrix} ight.

  • Câu 20: Nhận biết

    Chọn kết luận đúng

    Biết \overrightarrow{a}, \overrightarrow{b} \neq \overrightarrow{0} và \overrightarrow{a}.\overrightarrow{b} = - \left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|. Câu nào sau đây đúng?

    Ta có:

    \overrightarrow{a}.\overrightarrow{b} = - \left|\overrightarrow{a} \right|.\left| \overrightarrow{b} \right|

    \Leftrightarrow \left| \overrightarrow{a} \right|.\left|\overrightarrow{b} \right|\cos\left(\overrightarrow{a},\overrightarrow{b} \right) = - \left|\overrightarrow{a} \right|.\left| \overrightarrow{b}\right|

    \Leftrightarrow \cos\left( \overrightarrow{a},\overrightarrow{b} \right) = - 1 nên \overrightarrow{a}và \overrightarrow{b} ngược hướng

  • Câu 21: Vận dụng

    Tìm tập hợp điểm M

    Cho tam giác ABC. Tập hợp các điểm M thỏa mãn \overrightarrow{MA}.(\overrightarrow{MB}+\overrightarrow{MC})=0 là:

    Ta có: \overrightarrow {MB} + \overrightarrow {MC} = 2\overrightarrow {MI} (I là trung điểm của BC)

    \begin{matrix} \overrightarrow {MA} .\left( {\overrightarrow {MB} + \overrightarrow {MC} } ight) = 0 \hfill \\ \Leftrightarrow \overrightarrow {MA} .\left( {2\overrightarrow {MI} } ight) = 0 \hfill \\ \Leftrightarrow 2\overrightarrow {MA} .\overrightarrow {MI} = 0 \hfill \\ \Leftrightarrow \overrightarrow {MA} .\overrightarrow {MI} = 0 \hfill \\ \Rightarrow \cos \left( {\overrightarrow {MA} ,\overrightarrow {MI} } ight) = {90^0} \hfill \\ \Leftrightarrow \overrightarrow {MA} \bot \overrightarrow {MI} \hfill \\ \end{matrix}

    \Rightarrow \widehat {AMI} = {90^0}

    => Qũy tích điểm M là đường tròn đường kính IA.

  • Câu 22: Vận dụng

    Khẳng định nào sau đây đúng?

    Trong hệ tọa độ Oxy, cho bốn điểm A(3; - 2),\ B(7;1),\ C(0;1),\ D( - 8; - 5). Khẳng định nào sau đây đúng?

    Ta có \left\{ \begin{matrix} \overrightarrow{AB} = (4;3) \\ \overrightarrow{CD} = ( - 8; - 6) \\ \end{matrix} ight.\ \overset{}{ightarrow}\overrightarrow{CD} = - 2\overrightarrow{AB}\overset{}{ightarrow}\overrightarrow{AB},\ \overrightarrow{CD} ngược hướng.

  • Câu 23: Thông hiểu

    Tìm x thỏa mãn điều kiện

    Cho \overrightarrow{u} = 2\overrightarrow{i} - \overrightarrow{j} và \overrightarrow{v} = \overrightarrow{i} + x\overrightarrow{j}. Xác định x sao cho \overrightarrow{u} và \overrightarrow{v} cùng phương.

    Ta có \left\{ \begin{matrix} \overrightarrow{u} = 2\overrightarrow{i} - \overrightarrow{j}\overset{}{ightarrow}\overrightarrow{u} = (2;\ \ - 1) \\ \overrightarrow{v} = \overrightarrow{i} + x\overrightarrow{j}\overset{}{ightarrow}\overrightarrow{v} = (1;\ \ x) \\ \end{matrix} ight.\ .

    Để \overrightarrow{u} và \overrightarrow{v} cùng phương \Leftrightarrow \frac{1}{2} = \frac{x}{- 1} \Leftrightarrow x = - \frac{1}{2}.

  • Câu 24: Thông hiểu

    Xác định điểm M

    Cho hình bình hành ABCD, điểm M thỏa mãn: 4\overrightarrow{AM} = \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AC}. Khi đó điểm M là:

    Hình vẽ minh họa

    Ta có:

    \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AC} = \overrightarrow{AC} + \overrightarrow{AC} = 2\overrightarrow{AC} = 4\overrightarrow{AM}

  • Câu 25: Vận dụng

    Xét tính đúng sai của các khẳng định

    Cho tam giác ABC đều cạnh a, có trọng tâm G. Khi đó:

    a) \overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}. Đúng||Sai

    b) \overrightarrow{AB} - \overrightarrow{CB} = \overrightarrow{CA}. Sai||Đúng

    c) \left| \overrightarrow{AB} + \overrightarrow{AC} \right| = a\sqrt{3}. Đúng||Sai

    d) Tập hợp các điểm M thỏa mãn đẳng thức \left| \overrightarrow{MA} + \overrightarrow{MB} \right| = 2\left| \overrightarrow{MC} \right| là đường trung trực của đoạn IC. Đúng||Sai

    Đáp án là:

    Cho tam giác ABC đều cạnh a, có trọng tâm G. Khi đó:

    a) \overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}. Đúng||Sai

    b) \overrightarrow{AB} - \overrightarrow{CB} = \overrightarrow{CA}. Sai||Đúng

    c) \left| \overrightarrow{AB} + \overrightarrow{AC} \right| = a\sqrt{3}. Đúng||Sai

    d) Tập hợp các điểm M thỏa mãn đẳng thức \left| \overrightarrow{MA} + \overrightarrow{MB} \right| = 2\left| \overrightarrow{MC} \right| là đường trung trực của đoạn IC. Đúng||Sai

    a) Đúng

    Theo quy tắc 3 điểm ta luôn có \overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}. Vậy a đúng

    b) Sai

    Ta có: \overrightarrow{AB} - \overrightarrow{CB} = \overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}. Vậy b sai

    c) Đúng

    Vẽ hình bình hành ABDC, gọi H là giao điểm AD và BC

    Suy ra H là trung điểm của cả AD và BC.

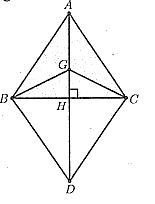
    A diagram of a triangle with a square and a square in the center with Great Pyramid of Giza in the backgroundDescription automatically generated

    Theo quy tắc hình bình hành: \overrightarrow{AB} + \overrightarrow{AC} = \overrightarrow{AD}. Ta có AH là đường cao của tam giác ABC nên AH = \sqrt{AB^{2} - BH^{2}} = \sqrt{a^{2} - \left( \frac{a}{2} \right)^{2}} = \frac{a\sqrt{3}}{2}

    Suy ra: AD = 2AH = a\sqrt{3}.

    Vậy \left| \overrightarrow{AB} + \overrightarrow{AC} \right| = \left| \overrightarrow{AD} \right| = AD = a\sqrt{3}. Vậy c đúng

    d) Đúng

    Gọi I là trung điểm AB, ta có:

    \left| \overrightarrow{MA} + \overrightarrow{MB} \right| = 2\left| \overrightarrow{MC} \right| \Leftrightarrow 2\left| \overrightarrow{MI} \right| = 2\left| \overrightarrow{MC} \right| \Leftrightarrow MI = MC.

    Điều đó chứng tỏ điểm M cách đều hai điểm I,\ \ C, nên tập hợp các điểm M là đường trung trực của đoạn IC. Vậy d đúng

  • Câu 26: Nhận biết

    Chọn phương án thích hợp

    Vectơ là một đoạn thẳng:

    Vectơ là một đoạn thẳng có hướng.

  • Câu 27: Nhận biết

    Tìm vị trí điểm I thỏa mãn hệ thức

    Cho hai điểm A và B phân biệt. Điều kiện để I là trung điểm AB là:

    Điều kiện để I là trung điểm AB là \overrightarrow{IA} = - \overrightarrow{IB}.

  • Câu 28: Nhận biết

    Chọn đáp án đúng

    Cho hình vuông ABCD, tính \cos\left( \overrightarrow{AB},\overrightarrow{CA} \right)?

    Đầu tiên ta đi tìm số đo của góc \left( \overrightarrow{AB},\overrightarrow{CA} \right) sau đó mới tính \cos\left( \overrightarrow{AB},\overrightarrow{CA} \right)

    Vì \left( \overrightarrow{AB},\overrightarrow{CA} \right) = 180^{o} - \left( \overrightarrow{AB},\overrightarrow{CA} \right) = 135^{o} \Rightarrow \cos\left( \overrightarrow{AB},\overrightarrow{CA} \right) = - \frac{\sqrt{2}}{2}.

  • Câu 29: Nhận biết

    Tìm khẳng định đúng

    Chọn khẳng định đúng.

    Hai vectơ cùng hướng và cùng độ dài thì bằng nhau.

  • Câu 30: Vận dụng cao

    Tính độ dài vectơ

    Cho hình thang vuông ABCD có \widehat{A} = \widehat{D} = 90^{0}. Tính độ dài vectơ \overrightarrow{\alpha} = \overrightarrow{DA} + \overrightarrow{DB} + \overrightarrow{DC}, biết AB = AD = 2,CD = 4.

    Hình vẽ minh họa

    Dựng hình bình hành ADBM ta có: \overrightarrow{DA} + \overrightarrow{DB} = \overrightarrow{DM}

    Do BM//DA nên BM\bot DC tại H,

    Tứ giác ADBH là hình vuông nên BH = 2, ta cũng tính được MH = 4.

    Dựng hình bình hành DMNC ta có: \overrightarrow{DA} + \overrightarrow{DB} + \overrightarrow{DC} = \overrightarrow{DN}.

    Gọi K là hình chiếu vuông góc của N lên DC. Ta chứng minh được HMNK là hình vuông.

    \Rightarrow HK = NK = 4,DK = 6

    Ta có: DN = \sqrt{DK^{2} + KN^{2}} = 2\sqrt{13}

  • Câu 31: Nhận biết

    Tìm tọa độ trung điểm

    Trong hệ tọa độ Oxy, cho hai điểm A(2; - 3),\ B(4;7). Tìm tọa độ trung điểm I của đoạn thẳng AB.

    Ta có \left\{ \begin{matrix} x_{I} = \frac{2 + 4}{2} = 3 \\ y_{I} = \frac{- 3 + 7}{2} = 2 \\ \end{matrix} ight.\ \overset{}{ightarrow}I(3;2).

  • Câu 32: Thông hiểu

    Khẳng định nào sau đây đúng?

    Cho hình bình hành ABCD có M là trung điểm của AB. Khẳng định nào sau đây đúng?

    Xét các đáp án ta thấy bài toán yêu cần phân tích vectơ \overrightarrow{DM} theo hai vectơ \overrightarrow{DC} và \overrightarrow{BC}.

    Vì ABCD là hình bình hành nên \overrightarrow{DB} = \overrightarrow{DA} + \overrightarrow{DC}.Vì M là trung điểm AB nên 2\ \overrightarrow{DM} = \overrightarrow{DA} + \overrightarrow{DB} \Leftrightarrow 2\ \overrightarrow{DM} = 2\ \overrightarrow{DA} + \overrightarrow{DC} \Leftrightarrow 2\ \overrightarrow{DM} = - \ 2\ \overrightarrow{BC} + \overrightarrow{DC}

    suy ra \overrightarrow{DM} = \frac{1}{2}\overrightarrow{DC} - \overrightarrow{BC}.

  • Câu 33: Thông hiểu

    Chọn đẳng thức đúng

    Cho 6 điểm phân biệt A, B, C, D, E, F. Đẳng thức nào sau đây đúng?

     Ta có:\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{FA}+\overrightarrow{BC}+\overrightarrow{EF}+\overrightarrow{DE}=\overrightarrow{0}\Leftrightarrow\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DE} + \overrightarrow {EF} + \overrightarrow {FA} = \overrightarrow 0.

  • Câu 34: Vận dụng

    Đẳng thức nào sau đây đúng?

    Cho hình thoi ABCD cạnh a và \widehat{BAD} = 60{^\circ}. Đẳng thức nào sau đây đúng?

    Vì tam giác BAD cân và \widehat{BAD} = 60{^\circ}, suy ra tam giác ABD đều cạnh a nên BD = a\overset{}{ightarrow}\left| \overrightarrow{BD} ight| = a.

  • Câu 35: Thông hiểu

    Xác định câu đúng

    Gọi AN,\ CM là các trung tuyến của tam giác ABC. Đẳng thức nào sau đây đúng?

    Hình vẽ minh họa:

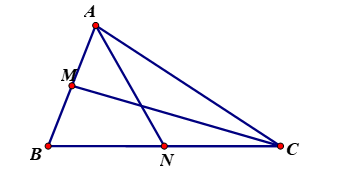
    Ta có \overrightarrow{AN} = \frac{1}{2}\left( \overrightarrow{AB} + \overrightarrow{AC} \right) = \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AC}

    \overrightarrow{CM} = \overrightarrow{CA} + \overrightarrow{AM} \Rightarrow \frac{1}{2}\overrightarrow{CM} = \frac{1}{2}\overrightarrow{CA} + \frac{1}{2}\overrightarrow{AM}

    Suy ra \overrightarrow{AN} + \frac{1}{2}\overrightarrow{CM} = \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AC} + \frac{1}{2}\overrightarrow{CA} + \frac{1}{2}\overrightarrow{AM}

    = \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AC} - \frac{1}{2}\overrightarrow{AC} + \frac{1}{2} \cdot \frac{1}{2}\overrightarrow{AB} = \frac{3}{4}\overrightarrow{AB}

    Do đó \overrightarrow{AB} = \frac{4}{3}\overrightarrow{AN} + \frac{2}{3}\overrightarrow{CM}.

  • Câu 36: Nhận biết

    Tìm tọa độ trung điểm đoạn AB

    Cho hai điểm A(4; - 1),B( - 2;5). Tọa độ trung điểm của đoạn AB là:

    Gọi M là trung điểm của đoạn thẳng AB. Khi đó tọa độ điểm M là:

    \left\{ \begin{matrix}x_{M} = \dfrac{4 + ( - 2)}{2} = 1 \\y_{M} = \dfrac{- 1 + 5}{2} = 2 \\\end{matrix} ight.\ \Rightarrow M(1;2)

  • Câu 37: Nhận biết

    Tìm độ dài đoạn thẳng AB

    Tính độ dài đoạn thẳng AB biết tọa độ A(1;1),B(4;5)?

    Ta có: AB = \sqrt{(4 - 1)^{2} + (5 - 1)^{2}} = 5

  • Câu 38: Nhận biết

    Tìm câu sai

    Chọn câu sai?

    Đáp án sai là: \left| \overrightarrow{0} \right| = 0,\left| \overrightarrow{PQ} \right| = \overrightarrow{PQ} vì \left| \overrightarrow{PQ} \right| = PQ .

  • Câu 39: Vận dụng cao

    Tìm tọa độ điểm M thõa mãn điều kiện

    Trong hệ tọa độ Oxy, cho ba điểm A(1;0),\ B(0;3) và C( - 3; - 5). Tìm điểm M thuộc trục hoành sao cho biểu thức P = \left| 2\overrightarrow{MA} - 3\overrightarrow{MB} + 2\overrightarrow{MC} ight| đạt giá trị nhỏ nhất.

    Ta có

    2\overrightarrow{MA} -3\overrightarrow{MB} + 2\overrightarrow{MC} =2\left(\overrightarrow{MI} + \overrightarrow{IA} ight) - 3\left(\overrightarrow{MI} + \overrightarrow{IB} ight) + 2\left(\overrightarrow{MI} + \overrightarrow{IC} ight),\ \forall I

    = \overrightarrow{MI} + 2\left( \overrightarrow{IA} - 3\overrightarrow{IB} + 2\overrightarrow{IC} ight),\ \forall I.

    Chọn điểm I sao cho 2\overrightarrow{IA} - 3\overrightarrow{IB} + 2\overrightarrow{IC} = \overrightarrow{0}. (*)

    Gọi I(x;y), từ (*) ta có

    \left\{ \begin{matrix}2(1 - x) - 3(0 - x) + 2( - 3 - x) = 0 \\2(0 - y) - 3(2 - y) + 2( - 5 - y) = 0 \\\end{matrix} \Leftrightarrow \left\{ \begin{matrix}x = - 4 \\y = - 16 \\\end{matrix} ight.\ ight.\ \Rightarrow I( - 4; - 16).

    Khi đó P = \left| 2\overrightarrow{MA} -3\overrightarrow{MB} + 2\overrightarrow{MC} ight|= \left|\overrightarrow{MI} ight| = MI.

    Để P nhỏ nhất \Leftrightarrow MI nhỏ nhất. Mà M thuộc trục hoành nên MI nhỏ nhất khi M là hình chiếu vuông góc của I lên trục hoành \overset{}{ightarrow}M( - 4;0).

  • Câu 40: Nhận biết

    Chọn khẳng định đúng

    Cho hình bình hành ABCD có tâmO. Khẳng định nào sau đây là đúng:

    Ta có: \overrightarrow{AB} - \overrightarrow{AC} = \overrightarrow{CB} = \overrightarrow{DA}.

Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 5 Vectơ Sách CTST Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
  • Điểm thưởng: 0
Làm lại
1
34 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Đề kiểm tra 45 phút Chương 5 Vectơ Sách CTST
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Tìm bài trong mục này
🖼️

Toán 10 - Chân trời sáng tạo
Xem thêm