Định lí Cosin và định lí Sin sách CTST
Trong tam giác 
\(ABC\) với \(BC=a,CA=b,AB=c\) ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A\\{b^2} = {c^2} + {a^2} - 2ca\cos B\\{c^2} = {a^2} + {b^2} - 2ab\cos C\end{array}\)
Hệ quả
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\)
Ví dụ: Cho tam giác \(ABC\) có \(b = 5, c = 7\) và \(\cos A = 3/5\). Tính cạnh \(a\) và cosin các góc còn lại của tam giác đó.
Hướng dẫn giải
Ta có:
\(\begin{matrix}
{a^2} = {b^2} + {c^2} - 2bc.\cos A \hfill \\
= 25 + 49 - 2.5.7.\dfrac{3}{5} = 32 \hfill \\
\Rightarrow a = \sqrt {32} = 4\sqrt 2 \hfill \\
\cos B = \dfrac{{{c^2} + {a^2} - {b^2}}}{{2ca}} = \dfrac{{32 + 49 - 25}}{{56\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2} \hfill \\
\cos C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}} = \dfrac{{32 + 25 - 49}}{{40\sqrt 2 }} = \dfrac{8}{{40\sqrt 2 }} = \dfrac{{\sqrt 2 }}{{10}} \hfill \\
\end{matrix}\)
2. Định lí sin
Trong tam giác \(ABC\) với \(BC=a,CA=b,AB=c\) ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.\)
(\(R\) là bán kính đường tròn ngoại tiếp tam giác \(ABC\))
Hệ quả
\(a = 2R.\sin A;\quad b = 2R\sin B;\quad c = 2R\sin C\)
\(\sin A = \frac{a}{{2R}};\quad \sin B = \frac{b}{{2R}};\quad \sin C = \frac{c}{{2R}}.\)
Ví dụ: Cho hình vẽ:
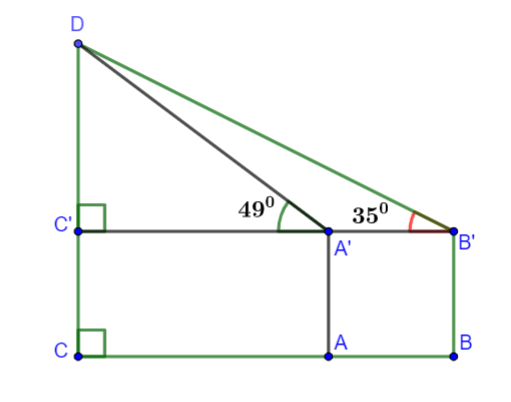
Biết: \(CC' = 1,3m\). Tính độ dài đoạn thẳng \(CD\)
Hướng dẫn giải
Ta có \(CC' = 1,3m\)
Áp dụng định lý sin trong tam giác A’B’D ta được:
\(\begin{matrix}
\dfrac{{B'D}}{{\sin \left( {{{180}^0} - \widehat {C'A'D}} \right)}} = \dfrac{{A'B'}}{{\sin \left( {{{180}^0} - \widehat {C'A'D} - {{35}^0}} \right)}} \hfill \\
\Leftrightarrow \dfrac{{B'D}}{{\sin {{131}^0}}} = \dfrac{{12}}{{\sin {{14}^0}}} \hfill \\
\Leftrightarrow B'D = \dfrac{{12.\sin {{131}^0}}}{{\sin {{14}^0}}} \hfill \\
\end{matrix}\)
Xét tam giác B’C’D ta có:
\(\begin{matrix}
C'D = B'D.\cos {35^0} \hfill \\
\Leftrightarrow C'D = \dfrac{{12.\sin {{131}^0}}}{{\sin {{14}^0}}}.\cos {35^0} \hfill \\
\Leftrightarrow C'D \approx 30,7\left( m \right) \hfill \\
\end{matrix}\)
3. Các công thức tính diện tích tam giác
\(1)\ S = \frac{1}{2}a{h_a} = \frac{1}{2}b{h_b} = \frac{1}{2}c{h_c}\)
\(2)\ S = \frac{1}{2}bc\sin A = \frac{1}{2}ca\sin B = \frac{1}{2}ab\sin C\)
\(3)\ S = \frac{{abc}}{{4R}}\)
\(4)\ S = pr = \frac{{(a + b + c).r}}{2}\)
\(5)\ S = \sqrt {p(p - a)(p - b)(p - c)}\) (Công thức Heron)
Ví dụ: Tính diện tích tam giác \(ABC\), biết chu vi tam giác bằng \(2p\), các góc \(\widehat A = α^0, \widehat B = β^0\).
Hướng dẫn giải
Ta có: \(S = \frac{{abc}}{{4R}}\)
Theo định lí sin ta có:
\(abc = 8{R^3}\sin \widehat A.\sin \widehat B.\sin \widehat C\)
\(=> S = 2{R^2}\sin \widehat A.\sin \widehat B.\sin \widehat C\)
\(R = \frac{a}{{\sin \widehat A}} = \frac{b}{{\sin \widehat B}} = \frac{c}{{\sin \widehat C}}\)
\(\Rightarrow R = \frac{{a + b + c}}{{\sin \widehat A + \sin \widehat B + \sin \widehat C}}\)
\(\Rightarrow R = \frac{{2p}}{{\sin \alpha + \sin \beta + \sin \left( {\pi - \alpha - \beta } \right)}}\)
\(\Rightarrow S = 2\left[ {\frac{{2p}}{{\sin \alpha + \sin \beta + \sin \left( {\alpha - \beta } \right)}}} \right]\)
