Tổng và hiệu của hai vectơ sách CTST
Định nghĩa
Cho hai vectơ 
\(\overrightarrow a\) và \(\overrightarrow b\). Với điểm A bất kì dựng \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b\). Khi đó \(\overrightarrow {AC}\) được gọi là vectơ tổng của hai vectơ \(\overrightarrow a\) và \(\overrightarrow b\).
Kí hiệu là \(\overrightarrow a + \overrightarrow b\)
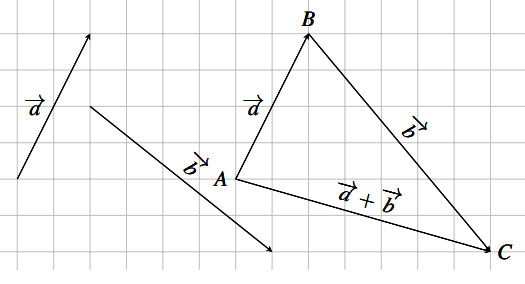
Nghĩa là: \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC}\)
Hình vẽ minh họa
Quy tắc ba điểmVới ba điểm M, N, P ta có: |
Định nghĩa
Cho hai vectơ \(\overrightarrow a\) và \(\overrightarrow b\). Phép trừ của hai vectơ \(\overrightarrow a\) và \(\overrightarrow b\) được định nghĩa là phép cộng của và .
Kí hiệu là \(\overrightarrow a - \overrightarrow b = \overrightarrow a + \left( { - \overrightarrow b } \right)\)
Ví dụ: Cho tam giác ABC. Xác định vectơ.
a) \(\overrightarrow a = \overrightarrow {AB} + \overrightarrow {BC}\)
b) \(\overrightarrow b = \overrightarrow {AB} - \overrightarrow {AC}\)
Hướng dẫn giải
Hình vẽ minh họa
a) \(\overrightarrow a = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC}\)
b) \(\overrightarrow b = \overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB}\)
B. Quy tắc hình bình hành
Hình vẽ minh họa
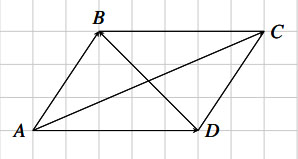
Cho ABCD là hình bình hành, ta có:
\(\begin{matrix}
\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \hfill \\
\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \hfill \\
\end{matrix}\)
Chú ý
Để áp dụng quy tắc hình bình hành, ta cần đưa bài toán tìm tổng hai vectơ về bài toán tìm tổng của hai vectơ có chung điểm đầu.
Ví dụ: Chứng minh rằng nếu tam giác ABC thỏa mãn \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|\) thì tam giác đó là tam giác vuông.
Hướng dẫn giải
Dựng hình bình hành ABCD.
Theo quy tắc hình hình hành ta có: \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD}\)
Theo quy tắc hiệu hai vectơ ta có: \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB}\)
Từ giả thiết suy ra: \(\left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {BC} } \right|\) tức là \(AD = BC\)
Hình bình hành ABCD có hai đường chéo bằng nhau nên nó là hình chữ nhật, tức ABC là tam giác vuông.
C. Tính chất của phép cộng, trừ hai vectơ
Tính chất giao hoán
\(\overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a\)
Tính chất kết hợp
\(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\)
Cộng với vectơ \(\overrightarrow 0\)
\(\overrightarrow a + \overrightarrow 0 = \overrightarrow 0 + \overrightarrow a = \overrightarrow a\)
Vectơ đối
| \(\overrightarrow 0 = - \overrightarrow 0\) |
\(\overrightarrow a - \overrightarrow b = - \left( {\overrightarrow b - \overrightarrow a } \right)\) |
| \(\overrightarrow {AB} = - \overrightarrow {BA}\) |
\(\overrightarrow a + \left( { - \overrightarrow a } \right) = \overrightarrow 0\) |
D. Tính chất vectơ của trung điểm đoạn thẳng và trọng tâm tam giác
Tính chất
Điểm M là trung điểm của đoạn thẳng AB khi và chỉ khi \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0\).
Điểm G là trọng tâm tam giác ABC khi và chỉ khi \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0\).
