Các phép toán trên tập hợp sách CTST
Cho hai tập hợp ![]() \(A\) và
\(A\) và ![]() \(B\). Tập hợp các phần tử thuộc
\(B\). Tập hợp các phần tử thuộc ![]() \(A\) hoặc thuộc
\(A\) hoặc thuộc ![]() \(B\) gọi là hợp của hai tập hợp
\(B\) gọi là hợp của hai tập hợp ![]() \(A\) và
\(A\) và ![]() \(B\), kí hiệu là
\(B\), kí hiệu là ![]() \(A \cup B\)
\(A \cup B\)
![]() \(A \cup B = \left\{ {x|x \in A \text{ } \text{hoặc}\text{ } x\in B} \right\}\)
\(A \cup B = \left\{ {x|x \in A \text{ } \text{hoặc}\text{ } x\in B} \right\}\)
Hình vẽ minh họa
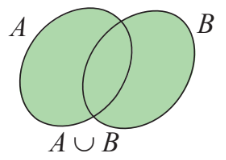
Cho hai tập hợp ![]() \(A\) và
\(A\) và ![]() \(B\). Tập hợp các phần tử thuộc
\(B\). Tập hợp các phần tử thuộc ![]() \(A\) và thuộc
\(A\) và thuộc ![]() \(B\) gọi là giao của hai tập hợp
\(B\) gọi là giao của hai tập hợp ![]() \(A\) và
\(A\) và ![]() \(B\), kí hiệu là
\(B\), kí hiệu là ![]() \(A \cap B\)
\(A \cap B\)
![]() \(A \cap B = \left\{ {x|x \in A,x \in B} \right\}\)
\(A \cap B = \left\{ {x|x \in A,x \in B} \right\}\)
Hình vẽ minh họa
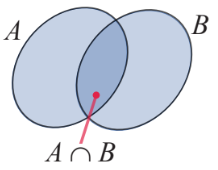
Ví dụ: Cho hai tập hợp ![]() \(A = \left\{ {1;2;3;5;7} \right\}\) và
\(A = \left\{ {1;2;3;5;7} \right\}\) và ![]() \(B = \{ n \in N|\)
\(B = \{ n \in N|\)![]() \(n\) là ước số của
\(n\) là ước số của ![]() \(12\}\). Tìm
\(12\}\). Tìm ![]() \(A \cup B\) và
\(A \cup B\) và ![]() \(A \cap B\)
\(A \cap B\)
Hướng dẫn giải
Ta có: ![]() \(B = \left\{ {1;2;3;4;6;12} \right\}\)
\(B = \left\{ {1;2;3;4;6;12} \right\}\)
![]() \(A \cap B = \left\{ {1;2;3} \right\}\)
\(A \cap B = \left\{ {1;2;3} \right\}\)
![]() \(A \cup B = \left\{ {1;2;3;4;5;6;7;12} \right\}\)
\(A \cup B = \left\{ {1;2;3;4;5;6;7;12} \right\}\)
Nhận xét
Nếu A và B là hai tập hợp hữu hạn thì:
 \(n(A \cup B) = n(A) + n(B) - n(A \cap B)\)
\(n(A \cup B) = n(A) + n(B) - n(A \cap B)\)- Nếu
 \(A \cap B = \varnothing\) thì
\(A \cap B = \varnothing\) thì  \(n(A \cup B) = n(A) + n(B)\)
\(n(A \cup B) = n(A) + n(B)\)
Ví dụ: Lớp 10A có 15 bạn thích môn Văn, 20 bạn thích môn Toán. Trong số các bạn thích văn
hoặc toán có 8 bạn thích cả 2 môn. Trong lớp vẫn còn 10 bạn không thích môn nào trong 2 môn Văn và Toán. Hỏi lớp 10A có bao nhiêu bạn.
Hướng dẫn giải
Sử dụng biểu đồ Ven để giải toán
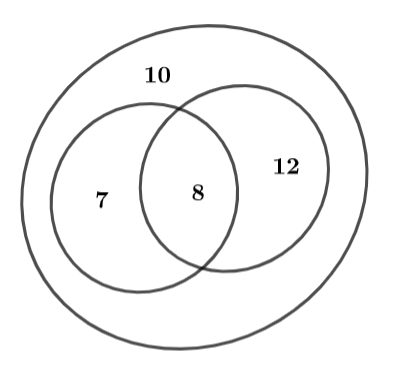
Ta có: Số bạn chỉ thích Văn là (bạn).
Số bạn chỉ thích Toán là 20 − 8 = 12 (bạn).
Số học sinh cả lớp là tổng các phần không giao nhau: 7 + 8 + 12 + 10 = 37.
Chú ý: Để tìm các tập hợp là hợp, giao, hiệu, phần bù của những tập con của tập số thực, ta thường sẽ vẽ sơ đồ trên trục số.
Ví dụ: Xác định các tập hợp sau đây bằng cách vẽ trục số:
a) ![]() \((0; 3) ∪ (−3; 2)\)
\((0; 3) ∪ (−3; 2)\)
b) ![]() \(A = \left \{ x ∈ \mathbb{R}||x +2| < 2 \right \} , B = \left \{ x ∈ \mathbb{R}||x +4| ≥ 3 \right \}\). Tìm
\(A = \left \{ x ∈ \mathbb{R}||x +2| < 2 \right \} , B = \left \{ x ∈ \mathbb{R}||x +4| ≥ 3 \right \}\). Tìm ![]() \(A∩B\).
\(A∩B\).
Hướng dẫn giải
a) Biểu diễn tập hợp ![]() \(A\) trên trục số.
\(A\) trên trục số.
Biểu diễn tập ![]() \(B\) trên trục số.
\(B\) trên trục số.
Hình vẽ minh họa
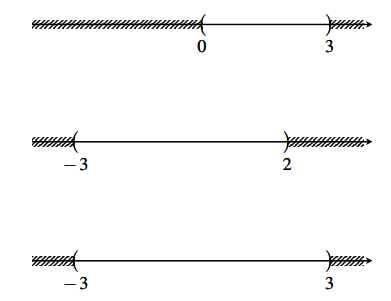
Kết hợp hai trục số trên ta được tập ![]() \(A∪B = (−3; 3)\)
\(A∪B = (−3; 3)\)
b) Ta có: ![]() \(|x+2| < 2 ⇔ −2 < x+2 < 2\)
\(|x+2| < 2 ⇔ −2 < x+2 < 2\) ![]() \(⇔ −4 < x < 0\)
\(⇔ −4 < x < 0\)
Do đó ![]() \(A = (−4; 0)|x+4| ≥ 3\)
\(A = (−4; 0)|x+4| ≥ 3\)
⇔ ![]() \(\left[ {\begin{array}{*{20}{l}}
{x + 4 \leqslant - 3} \\
{x + 4 \geqslant 3}
\end{array}} \right.\)
\(\left[ {\begin{array}{*{20}{l}}
{x + 4 \leqslant - 3} \\
{x + 4 \geqslant 3}
\end{array}} \right.\)
⇔ ![]() \(\left[ {\begin{array}{*{20}{l}}
{x \leqslant - 7} \\
{x \geqslant - 1}
\end{array}} \right.\)
\(\left[ {\begin{array}{*{20}{l}}
{x \leqslant - 7} \\
{x \geqslant - 1}
\end{array}} \right.\)
Do đó ![]() \(B = (−∞;−7]∪[−1;+∞)\)
\(B = (−∞;−7]∪[−1;+∞)\)
Biểu diễn tập A trên trục số
Biểu diễn tập B trên trục số
Hình vẽ minh họa
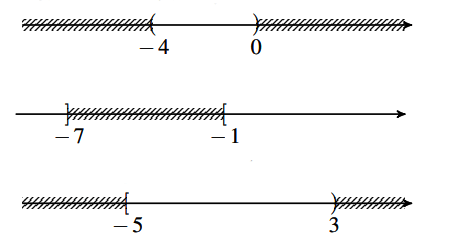
Biểu diễn tập C trên trục số => ![]() \(A \cap B = \left[ { - 5;3} \right)\)
\(A \cap B = \left[ { - 5;3} \right)\)
2. Hiệu của hai tập hợp, phần bù của tập con
Cho hai tập hợp ![]() \(A\) và
\(A\) và ![]() \(B\). Tập hợp các phần tử thuộc
\(B\). Tập hợp các phần tử thuộc ![]() \(A\) nhưng không thuộc
\(A\) nhưng không thuộc ![]() \(B\) gọi là hiệu của hai tập hợp
\(B\) gọi là hiệu của hai tập hợp ![]() \(A\) và
\(A\) và ![]() \(B\), kí hiệu là
\(B\), kí hiệu là ![]() \(A \setminus B\).
\(A \setminus B\).
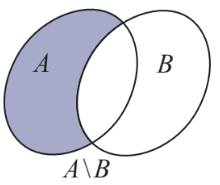
![]() \(A\setminus B = \left \{ x|x ∈ A \text{ }\text{và} \text{ } x ∉ B \right \}\)
\(A\setminus B = \left \{ x|x ∈ A \text{ }\text{và} \text{ } x ∉ B \right \}\)
Hình vẽ minh họa
Cho hai tập hợp ![]() \(A\) và
\(A\) và ![]() \(E\). Nếu
\(E\). Nếu ![]() \(A\) là tập con của
\(A\) là tập con của ![]() \(E\) thì hiệu
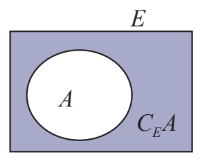
\(E\) thì hiệu ![]() \(E\setminus A\) gọi là phần bù của
\(E\setminus A\) gọi là phần bù của ![]() \(A\) trong
\(A\) trong ![]() \(E\), kí hiệu
\(E\), kí hiệu ![]() \({C_E}A\)
\({C_E}A\)
Hình vẽ minh họa
Ví dụ: ![]() \({C_\mathbb{Z}}\mathbb{N} = \mathbb{Z}{\rm{\backslash }}\mathbb{N} = \{ x|x \in \mathbb{Z}\) và
\({C_\mathbb{Z}}\mathbb{N} = \mathbb{Z}{\rm{\backslash }}\mathbb{N} = \{ x|x \in \mathbb{Z}\) và ![]() \(x \notin \mathbb{N}\} = \{ ...; - 3; - 2; - 1\}\)
\(x \notin \mathbb{N}\} = \{ ...; - 3; - 2; - 1\}\)
Đặc biệt: ![]() \({C_S}S = \varnothing\)
\({C_S}S = \varnothing\)
Ví dụ: Xác định tập hợp ![]() \((0; 3) \setminus (2; 4)\) và biểu diễn chúng trên trục số.
\((0; 3) \setminus (2; 4)\) và biểu diễn chúng trên trục số.
Hướng dẫn giải
Để xác định tập hợp ta biểu diễn trục số như sau:
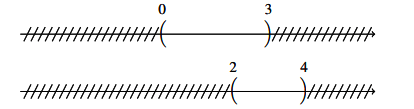
=> ![]() \((0; 3)\setminus (2; 4) = (0; 2]\)
\((0; 3)\setminus (2; 4) = (0; 2]\)
Ví dụ: Cho hai tập hợp ![]() \(A = \left \{ x ∈ \mathbb{R}|1 < x ≤ 4 \right \} , B = \left \{ x ∈ \mathbb{R}| −3 < x \right \}\). Tìm
\(A = \left \{ x ∈ \mathbb{R}|1 < x ≤ 4 \right \} , B = \left \{ x ∈ \mathbb{R}| −3 < x \right \}\). Tìm ![]() \(C_BA\).
\(C_BA\).
Hướng dẫn giải
Để xác định tập hợp ta biểu diễn trục số như sau:
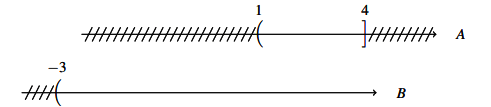
=> ![]() \(C_BA = (−3; 1]∪(4;+∞)\)
\(C_BA = (−3; 1]∪(4;+∞)\)





