Xác định phương trình đường tròn
Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?
Ta có:
Vậy phương trình đường tròn cần tìm là: .
Đề kiểm tra 45 phút Toán 10 Chương 9 Phương pháp tọa độ trong mặt phẳng sách Chân trời sáng tạo giúp bạn học tổng hợp lại kiến thức của cả nội dung chương. Cùng nhau luyện tập nha!
Xác định phương trình đường tròn
Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?
Ta có:
Vậy phương trình đường tròn cần tìm là: .
Tìm tập hợp điểm M thỏa mãn
Cho tam giác đều ![]() cạnh
cạnh ![]() trọng tâm
trọng tâm ![]() Tập hợp các điểm
Tập hợp các điểm ![]() thỏa mãn
thỏa mãn ![]() là
là
Gọi lần lượt là trung điểm của
Khi đó
Theo bài ra, ta có
Vậy tập hợp các điểm thỏa mãn
là đường trung trực của đoạn thẳng
cũng chính là đường trung trực của đoạn thẳng
vì
là đường trung bình của tam giác
Tìm tọa độ điểm M thõa mãn điều kiện
Trong hệ tọa độ ![]() cho ba điểm
cho ba điểm ![]() và
và ![]() Tìm điểm
Tìm điểm ![]() thuộc trục hoành sao cho biểu thức
thuộc trục hoành sao cho biểu thức ![]() đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
Ta có
Chọn điểm sao cho
Gọi , từ
ta có
Khi đó
Để nhỏ nhất
nhỏ nhất. Mà
thuộc trục hoành nên
nhỏ nhất khi
là hình chiếu vuông góc của
lên trục hoành
Tính độ dài vectơ
Cho tam giác ![]() có
có ![]() . Gọi các vectơ
. Gọi các vectơ ![]() theo thư tự là các vectơ có giá vuông góc với các đường thẳng
theo thư tự là các vectơ có giá vuông góc với các đường thẳng ![]() và
và ![]() . Tính độ dài vectơ
. Tính độ dài vectơ ![]() , biết
, biết ![]() .
.
Hình vẽ minh họa:
Gọi D là điểm thuộc miền trong tam giác ABC, dựng các vectơ dựng hình chữ nhật DGHE ta có:
Ta lại có:
Mặt khác
=> Ba điểm H, D, F thẳng hàng.
Khi đó:
Tìm điều kiện để hai vectơ bằng nhau
Cho các vectơ ![]() . Điều kiện để vectơ
. Điều kiện để vectơ ![]() là:
là:
Ta có: .
Tìm đường thẳng song song
Đường thẳng nào sau đây song song với đường thẳng ![]() ?
?
Xét đáp án: Chọn đáp án này.
Để ý rằng một đường thẳng song song với sẽ có dạng
Do đó kiểm tra chỉ thấy có đáp án
thỏa mãn, các đáp án còn lại không thỏa mãn.
Xác định vectơ chỉ phương của đường thẳng
Một vectơ chỉ phương của đường thẳng ![]() là:
là:
Đường thẳng có một vectơ chỉ phương là:
Viết phương trình tiếp tuyến của đường tròn
Viết phương trình tiếp tuyến ![]() của đường tròn
của đường tròn ![]() , biết tiếp tuyến đi qua điểm
, biết tiếp tuyến đi qua điểm ![]() .
.
Đường tròn (C) có tâm và tiếp tuyến có dạng
Ta có:
Xác định tập hợp điểm M thỏa mãn yêu cầu bài toán
Cho tam giác ![]() . Tập hợp những điểm
. Tập hợp những điểm ![]() sao cho:
sao cho: ![]() là:
là:
Gọi lần lượt là trung điểm của
và
.
Khi đó:
Vậy nằm trên đường trung trực của
.
Tìm mệnh đề đúng
Cho Hypebol ![]() có phương trình chính tắc là
có phương trình chính tắc là ![]() , với
, với ![]() . Khi đó khẳng định nào sau đây đúng?
. Khi đó khẳng định nào sau đây đúng?
Khẳng định đúng là: Nếu thì
có các tiêu điểm là
,
.
Tìm điểm thuộc đường thẳng
Cho đường thẳng ![]() . Điểm nào dưới đây thuộc đường thẳng đã cho?
. Điểm nào dưới đây thuộc đường thẳng đã cho?
Thay vào đường thẳng
suy ra
Vậy điểm thuộc đường thẳng
.
Tìm tọa độ trọng tâm
Trong hệ tọa độ ![]() cho tam giác
cho tam giác ![]() có
có ![]() Tìm tọa độ trọng tâm
Tìm tọa độ trọng tâm ![]() của tam giác
của tam giác ![]()
Ta có
Viết phương trình tiếp tuyến của đường tròn
Cho phương trình đường tròn ![]() . Viết phương trình tiếp tuyến của đường tròn
. Viết phương trình tiếp tuyến của đường tròn ![]() biết rằng tiếp tuyến vuông góc với đường thẳng
biết rằng tiếp tuyến vuông góc với đường thẳng ![]() ?
?
Đường tròn (C) có tâm
Vì vuông góc với đường thẳng
nên phương trình
có dạng
Vì là tiếp tuyến của (C) nên ta có:
Với thì phương trình
là
Với thì phương trình
là
Xét tính đúng sai của các khẳng định
Cho hình chữ nhật ![]() có
có ![]() . Gọi
. Gọi ![]() và
và ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() và
và ![]() .
.
a) ![]() . Đúng||Sai
. Đúng||Sai
b) ![]() . Đúng||Sai
. Đúng||Sai
c) ![]() . Sai||Đúng
. Sai||Đúng
d) Tìm tập hợp các điểm ![]() trong mặt phẳng thỏa mãn
trong mặt phẳng thỏa mãn ![]() là một đường thẳng. Sai||Đúng
là một đường thẳng. Sai||Đúng
Cho hình chữ nhật ![]() có
có ![]() . Gọi
. Gọi ![]() và
và ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() và
và ![]() .
.
a) ![]() . Đúng||Sai
. Đúng||Sai
b) ![]() . Đúng||Sai
. Đúng||Sai
c) ![]() . Sai||Đúng
. Sai||Đúng
d) Tìm tập hợp các điểm ![]() trong mặt phẳng thỏa mãn
trong mặt phẳng thỏa mãn ![]() là một đường thẳng. Sai||Đúng
là một đường thẳng. Sai||Đúng
a) Đúng
Hình vẽ minh họa
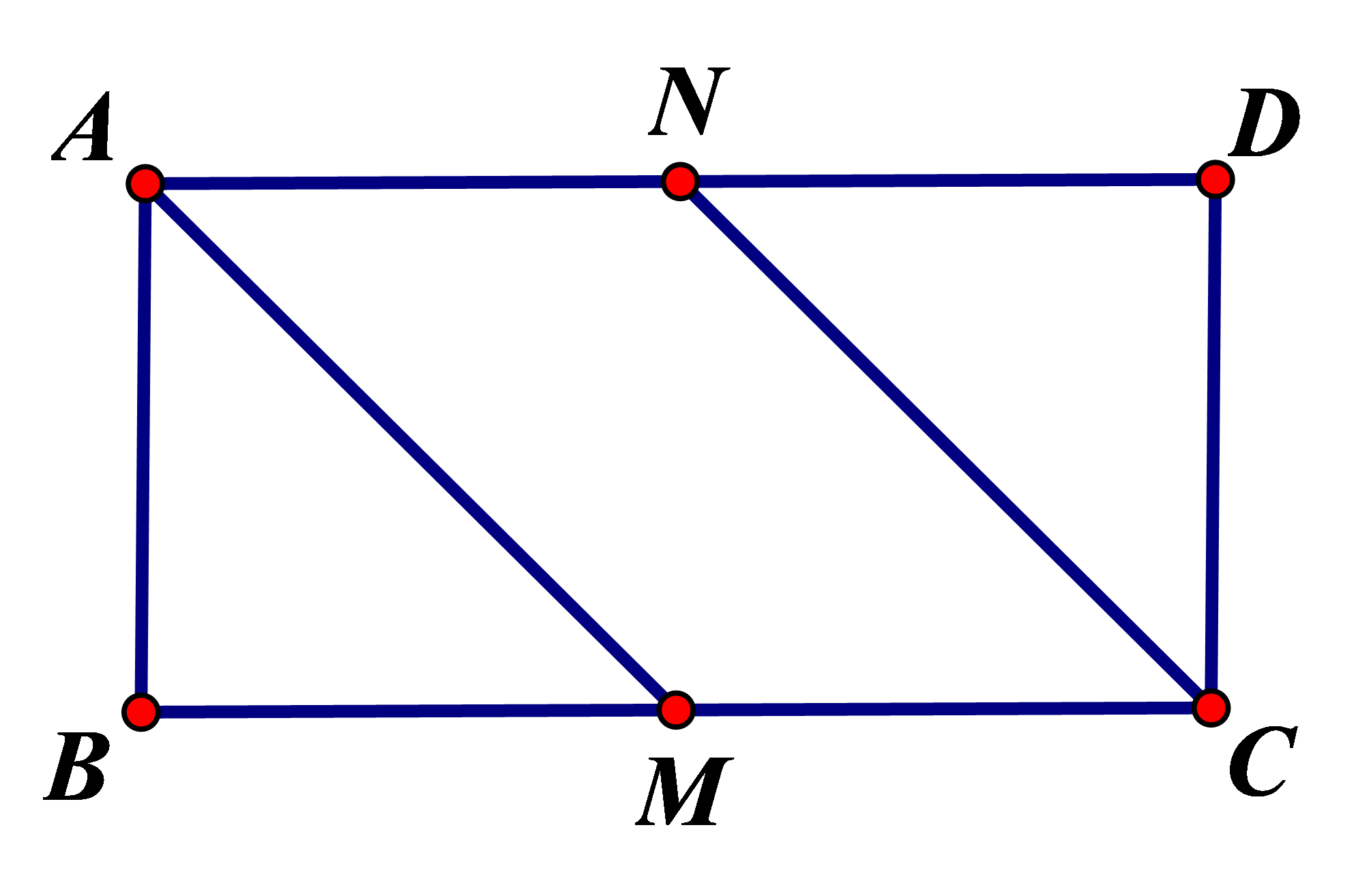
b) Đúng
Dễ thấy là hình bình hành nên
Mà là hình chữ nhật nên
.
Do đó:
c) Sai
Ta có:
d) Sai
Ta có:
.
Tập hợp điểm là đường tròn tâm
bán kính bằng
Chọn phương trình đường thẳng đúng
Cho hai điểm ![]() . Đường thẳng nào sau đây cách đều hai điểm
. Đường thẳng nào sau đây cách đều hai điểm ![]() ?
?
Gọi đường thẳng cần tìm là đường thẳng d.
Khi đó đường thẳng d cách đều hai điểm C và D khi:
TH1: Đường thẳng đó song song hoặc trùng với đường thẳng CD,
Ta có: nên một vectơ pháp tuyến của CD là
Vậy trong các đường thẳng đã cho chỉ có đường thẳng .
TH2: d là đường trung trực của CD.
Khi đó d đi qua trung điểm của CD và nhận
làm VTPT.
Suy ra phương trình đường thẳng d là:
Vậy đáp án là
Xác định phương trình đường thẳng BC
Cho tam giác ![]() có phương trình các cạnh
có phương trình các cạnh ![]() lần lượt là
lần lượt là ![]() và trực tâm
và trực tâm ![]() . Phương trình tổng quát của cạnh
. Phương trình tổng quát của cạnh ![]() là:
là:
Ta có: nên tọa độ điểm A là nghiệm hệ phương trình:
Ta có
Điểm
Ta có: nên tọa độ điểm B là nghiệm hệ phương trình:
Đường thẳng BC đi qua điểm B nhận làm vecto pháp tuyến có phương trình là:
Tìm vectơ cùng hướng
Cho ![]() không cùng phương,
không cùng phương, ![]() . Vectơ cùng hướng với
. Vectơ cùng hướng với ![]() là:
là:
Ta có. Chọn
.
Tìm phương trình chính tắc của elip
Hãy viết phương trình chính tắc của elip nếu nó đi qua điểm ![]() và tỉ số của tiêu cự với độ dài trục lớn bằng
và tỉ số của tiêu cự với độ dài trục lớn bằng ![]() .
.
Gọi phương trình chính tắc của Elip là với
Elip đi qua điểm
suy ra
Tỉ số của tiêu cực với độ dài trục lớn bằng
suy ra
Kết hợp với điều kiện ta được
Từ suy ra
Vậy phương trình cần tìm là
Viết phương trình tham số của đường thẳng
Viết phương trình tham số của đường thẳng đi qua hai điểm ![]() và
và ![]() .
.
Xác định vectơ theo yêu cầu
Cho bốn điểm ![]() phân biệt. Khi đó vectơ
phân biệt. Khi đó vectơ ![]() bằng:
bằng:
Ta có:
.
Cặp vectơ nào sau đây cùng phương?
Cho tam giác ![]() và đặt
và đặt ![]() Cặp vectơ nào sau đây cùng phương?
Cặp vectơ nào sau đây cùng phương?
Dễ thấy hai vectơ
cùng phương.
Chọn đẳng thức đúng
Gọi ![]() là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng![]() . Đẳng thức nào sau đây là đúng?
. Đẳng thức nào sau đây là đúng?
Hình vẽ minh họa:
![]()
Ta có: .
Tính góc giữa hai đường thẳng
Tính góc tạo bởi giữa hai đường thẳng ![]() và
và ![]()
Tìm m để ba điểm thẳng hàng
Trong mặt phẳng ![]() , cho
, cho ![]() . Tìm giá trị
. Tìm giá trị ![]() để
để ![]() là ba điểm thẳng hàng?
là ba điểm thẳng hàng?
Ta có: ,
Ba điểm thẳng hàng khi và chỉ khi
cùng phương với
.
Tìm tọa độ tâm và bán kính
Tọa độ tâm ![]() và bán kính
và bán kính ![]() của đường tròn
của đường tròn ![]() là:
là:
Ta có:
Tìm vectơ
Cho ![]() và điểm O. Gọi M, N lần lượt là hai điểm thỏa mãn
và điểm O. Gọi M, N lần lượt là hai điểm thỏa mãn ![]() và
và ![]() . Tìm
. Tìm ![]() .
.
Ta có:
Chọn dạng phương trình đúng
Dạng chính tắc của parabol là?
Dạng chính tắc của Parabol: .
Tìm phương trình đường phân giác
Trong mặt phẳng với hệ tọa độ ![]() , cho hai đường thẳng
, cho hai đường thẳng ![]() và
và ![]() . Phương trình đường phân giác góc nhọn tạo bởi hai đường thẳng
. Phương trình đường phân giác góc nhọn tạo bởi hai đường thẳng ![]() và
và ![]() là:
là:
Các đường phân giác của các góc tạo bởi và
là:
Gọi
Gọi là hình chiếu của
lên
Ta có: suy ra
Suy ra là đường phân giác góc tù, suy ra đường phân giác góc nhọn là
.
Mệnh đề nào sau đây đúng?
Gọi ![]() lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh ![]() và
và ![]() của tứ giác
của tứ giác ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
Do M là trung điểm các cạnh AB nên .
Do N lần lượt là trung điểm các cạnh DC nên .
Ta có
Mặt khác
Do đó .
Chọn đáp án đúng
Cho tam giác ![]() có
có ![]() là một đường trung tuyến. Biểu diễn vectơ
là một đường trung tuyến. Biểu diễn vectơ ![]() theo hai vectơ
theo hai vectơ ![]() và
và ![]() .
.
Vì là trung điểm
nên
.
Tìm m để có phương trình đường tròn
Cho phương trình ![]() . Tìm điều kiện của
. Tìm điều kiện của ![]() để
để ![]() là phương trình đường tròn.
là phương trình đường tròn.
Ta có:
Viết phương trình tham số của đường thẳng
Phương trình tham số của đường thẳng đi qua hai điểm ![]() là:
là:
Vectơ chỉ phương:
Đường thẳng đi qua điểm và có vectơ chỉ phương
nên có phương trình tham số là:
Tính khoảng cách từ điểm đến đường thẳng
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 2x + 3y + 5 = 0 và A(1; –3). Khoảng cách từ điểm A đến đường thẳng d là:
Ta có: .
Chọn đẳng thức đúng
Cho 4 điểm ![]() . Đẳng thức nào sau đây đúng.
. Đẳng thức nào sau đây đúng.
Ta có:
.
Biểu diễn một vectơ theo hai vectơ khác
Cho tam giác ![]() điểm
điểm ![]() thuộc cạnh
thuộc cạnh ![]() sao cho
sao cho ![]() và
và ![]() là trung điểm của
là trung điểm của ![]() Tính
Tính ![]() theo
theo ![]() và
và ![]()
Vì là trung điểm
nên
Suy ra
Viết phương trình tham số của d
Xác định phương trình tham số của đường thẳng ![]() . Biết rằng
. Biết rằng ![]() đi qua điểm
đi qua điểm ![]() và có một vectơ chỉ phương là
và có một vectơ chỉ phương là ![]() ?
?
Đường thẳng đi qua điểm và nhận
làm vectơ chỉ phương sẽ có phương trình tham số là:
.
Áp dụng với dữ kiện bài toan trên ta được:
Tính góc giữa hai đường thẳng
Gọi ![]() là góc tạo bởi hai đường thẳng
là góc tạo bởi hai đường thẳng ![]() và
và ![]() . Khi đó độ lớn của
. Khi đó độ lớn của ![]() bằng:
bằng:
Ta có:
Vậy góc tạo bởi hai đường thẳng bằng .
Tính giá trị của x
Cho hai điểm A(6; –1) và B(x; 9). Giá trị của x để khoảng cách giữa A và B bằng ![]() là:
là:
Ta có:
Tỉ số giữa độ dài trục ảo và độ dài trục thực
Cho hypebol (H): ![]() . Tỉ số giữa độ dài trục ảo và độ dài trục thực bằng:
. Tỉ số giữa độ dài trục ảo và độ dài trục thực bằng:
Ta có:
Ta có: a = 6; b =3
=> Độ dài trục ảo là 6, độ dài trục thực là 12
=> Tỉ số giữa độ dài trục ảo và độ dài trục thực là:
Tìm phương trình chính tắc của elip
Lập phương trình chính tắc của Elip đi qua điểm ![]() và có tâm sai
và có tâm sai ![]() .
.
Phương trình chính tắc của Elip có dạng: .
Elip đi qua điểm nên
.
Tâm sai .
.
Vậy phương trình chính tắc của Elip cần tìm là .
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
