Hệ bất phương trình bậc nhất hai ẩn sách CTST
Định nghĩa
Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn ![]() \(x, y\).
\(x, y\).
Mỗi nghiệm chung của tất cả các bất phương trình đó được gọi là một nghiệm của hệ bất phương trình đã cho.
Ví dụ:  \(\left\{ \begin{array}{l}2x + 3y > 10\\x - y \le 7\end{array} \right.;\left\{ \begin{array}{l}x + 3y \le 5\\x - 2y > 7\\2x > 3\end{array} \right.\)
\(\left\{ \begin{array}{l}2x + 3y > 10\\x - y \le 7\end{array} \right.;\left\{ \begin{array}{l}x + 3y \le 5\\x - 2y > 7\\2x > 3\end{array} \right.\)
- Cặp số
 \(({x_0};{y_0})\) là nghiệm của một hệ bất phương trình bậc nhất hai ẩn khi
\(({x_0};{y_0})\) là nghiệm của một hệ bất phương trình bậc nhất hai ẩn khi  \(({x_0};{y_0})\) đồng thời là nghiệm của tất cả các ất phương trình trong hệ đó.
\(({x_0};{y_0})\) đồng thời là nghiệm của tất cả các ất phương trình trong hệ đó.
Ví dụ: Cặp số ![]() \((7;0)\) là một nghiệm của hệ bất phương trình
\((7;0)\) là một nghiệm của hệ bất phương trình ![]() \(\left\{ \begin{array}{l}2x + 3y > 10\\x - y \le 7\end{array} \right.\).
\(\left\{ \begin{array}{l}2x + 3y > 10\\x - y \le 7\end{array} \right.\).
2. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn
Trên mặt phẳng tọa độ ![]() \(Oxy\), tập hợp các điểm
\(Oxy\), tập hợp các điểm ![]() \((x_0; y_0)\) có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn được gọi là miền nghiệm của hệ bất phương trình đó.
\((x_0; y_0)\) có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn được gọi là miền nghiệm của hệ bất phương trình đó.
Miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.
Biểu diễn miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn:
Bước 1: Trên cùng một mặt phẳng tọa độ, biểu diễn miền nghiệm của mỗi bất phương trình của hệ.
Bước 2: Phần giao của các miền nghiệm là miền nghiệm của hệ bất phương trình.
|
Chi tiết cách biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn.
|
Ví dụ: Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn sau
![]() \(\left\{ \begin{gathered}
x + y > 1 \hfill \\
x - y < 2\; \hfill \\
\end{gathered} \right.\)
\(\left\{ \begin{gathered}
x + y > 1 \hfill \\
x - y < 2\; \hfill \\
\end{gathered} \right.\)
Hướng dẫn giải
Vẽ các đường thẳng ![]() \(\left\{ {\begin{array}{*{20}{c}}
{{d_1}:x + y = 1} \\
{{d_2}:x - y = 2}
\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}
{{d_1}:x + y = 1} \\
{{d_2}:x - y = 2}
\end{array}} \right.\)
Vì điểm ![]() \(M0;2)\) có tọa độ thỏa mãn các bất phương trình trong hệ nên ta tô đậm các nửa mặt phẳng bờ
\(M0;2)\) có tọa độ thỏa mãn các bất phương trình trong hệ nên ta tô đậm các nửa mặt phẳng bờ ![]() \({d_1};{d_2}\) không chứa
\({d_1};{d_2}\) không chứa ![]() \(M\).
\(M\).
Miền không bị tô đậm trong hình vẽ và không chứa các tia giới hạn miền là nghiệm của hệ đã cho.
Hình vẽ minh họa

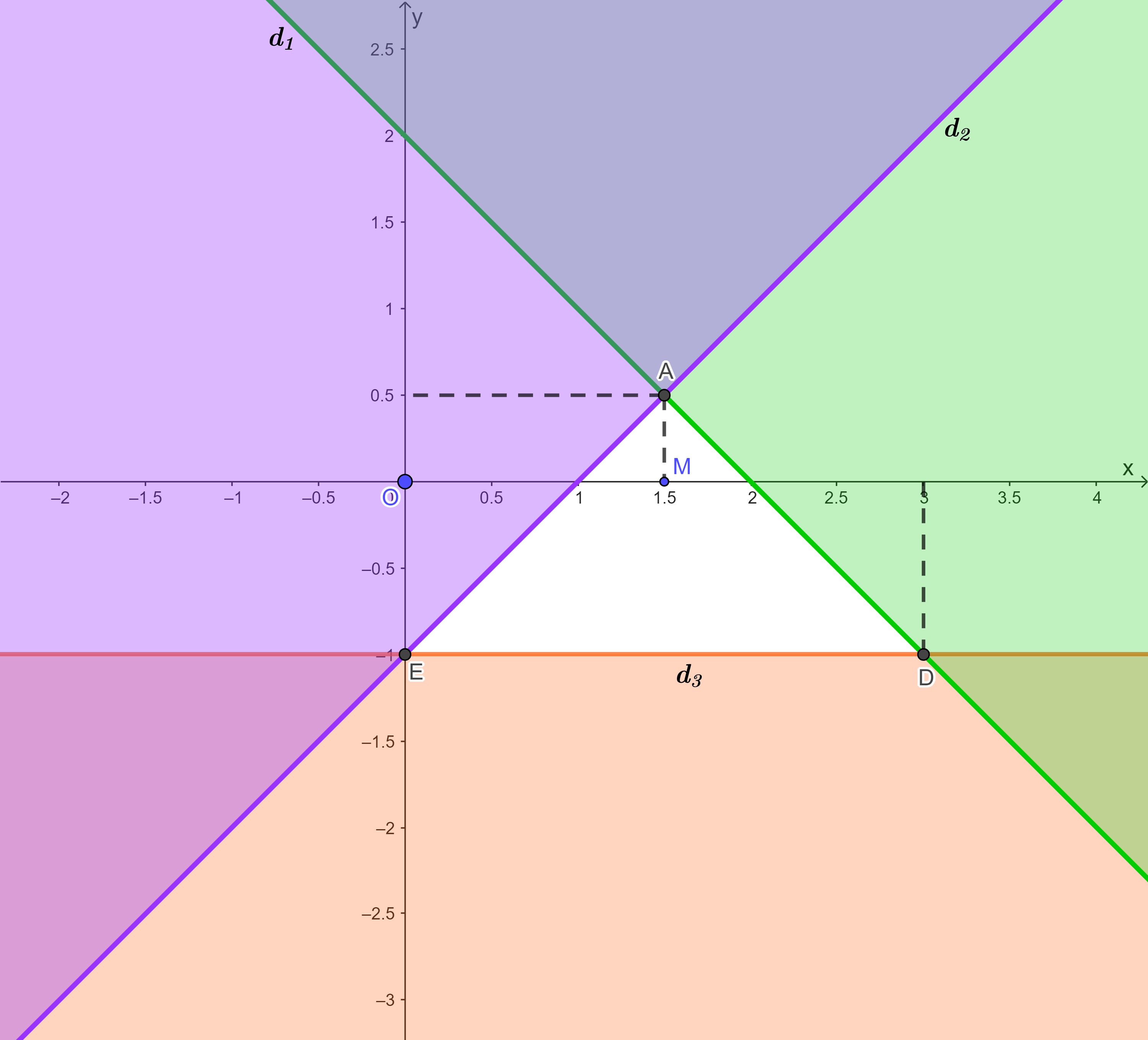
Ví dụ: Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn sau:
 \(\left\{ {\begin{array}{*{20}{c}}
{x + y < 2} \\
{x - y > 1} \\
{y > 1}
\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}
{x + y < 2} \\
{x - y > 1} \\
{y > 1}
\end{array}} \right.\)
Hướng dẫn giải
Vẽ các đường thẳng  \(\left\{ {\begin{array}{*{20}{c}}
{{d_1}:x + y = 2} \\
{{d_2}:x - y = 1} \\
{{d_3}:y = - 1}
\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}
{{d_1}:x + y = 2} \\
{{d_2}:x - y = 1} \\
{{d_3}:y = - 1}
\end{array}} \right.\)
Vì điểm ![]() \(M\left( {\frac{3}{2};0} \right)\) có tọa độ thỏa mãn các bất phương trình trong hệ nên ta tô đậm các nửa mặt phẳng bờ
\(M\left( {\frac{3}{2};0} \right)\) có tọa độ thỏa mãn các bất phương trình trong hệ nên ta tô đậm các nửa mặt phẳng bờ ![]() \({d_1};{d_2};{d_3}\) không chứa
\({d_1};{d_2};{d_3}\) không chứa ![]() \(M\).
\(M\).
Miền không bị tô đậm trong hình vẽ và không chứa các đoạn giới hạn miền là nghiệm của hệ đã cho.
Hình vẽ minh họa
3. Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của biểu thức F = ax + by trên một miền đa giác
Cho hệ bất phương trình bậc nhất hai ẩn ![]() \(x, y\) có miền nghiệm là miền đa giác
\(x, y\) có miền nghiệm là miền đa giác ![]() \({A_1}{A_2}...{A_n}.\)
\({A_1}{A_2}...{A_n}.\)
Khi đó: Giá trị lớn nhất (hay nhỏ nhất) của biểu thức ![]() \(F(x;y) = mx + ny\), với
\(F(x;y) = mx + ny\), với ![]() \((x;y)\) là tọa độ các điểm thuộc miền đa giác
\((x;y)\) là tọa độ các điểm thuộc miền đa giác ![]() \({A_1}{A_2}...{A_n}\), đạt được tại một trong các đỉnh của đa giác đó.
\({A_1}{A_2}...{A_n}\), đạt được tại một trong các đỉnh của đa giác đó.
Ví dụ: Một công ty cần thuê xe để chở 150 người và 10 tấn hàng. Hiện tại bên cho thuê xe có hai loại xe ![]() \(M\) có 10 chiếc và xe
\(M\) có 10 chiếc và xe ![]() \(N\) có 9 chiếc. Giá thuê một chiếc xe
\(N\) có 9 chiếc. Giá thuê một chiếc xe ![]() \(M\) là 4 triệu, một chiếc xe
\(M\) là 4 triệu, một chiếc xe ![]() \(N\) cho thuê với giá 3 triệu đồng. Hỏi phải thuê bao nhiêu chiếc xe mỗi loại để chi phí bỏ ra là nhỏ nhất? Biết rằng mỗi xe loại
\(N\) cho thuê với giá 3 triệu đồng. Hỏi phải thuê bao nhiêu chiếc xe mỗi loại để chi phí bỏ ra là nhỏ nhất? Biết rằng mỗi xe loại ![]() \(M\) có thể chở tối đa 20 người và 0,8 tấn hàng, mỗi xe loại
\(M\) có thể chở tối đa 20 người và 0,8 tấn hàng, mỗi xe loại ![]() \(N\) có thể chở tối đa được 10 người và 2 tấn hàng.
\(N\) có thể chở tối đa được 10 người và 2 tấn hàng.
Hướng dẫn giải
Gọi ![]() \(x, y\) lần lượt là số xe loại
\(x, y\) lần lượt là số xe loại ![]() \(M\) và
\(M\) và ![]() \(N\). Khi đó số tiền cần bỏ ra để thuê xe là
\(N\). Khi đó số tiền cần bỏ ra để thuê xe là ![]() \(f(x; y) = 4x+3y\).
\(f(x; y) = 4x+3y\).
Điều kiện: ![]() \(\left\{ \begin{gathered}
0 \leqslant x \leqslant 10 \hfill \\
0 \leqslant y \leqslant 9 \hfill \\
\end{gathered} \right.\),
\(\left\{ \begin{gathered}
0 \leqslant x \leqslant 10 \hfill \\
0 \leqslant y \leqslant 9 \hfill \\
\end{gathered} \right.\), ![]() \(x;y \in \mathbb{Z}\)
\(x;y \in \mathbb{Z}\)
Ta có: ![]() \(x\) xe loại
\(x\) xe loại ![]() \(M\) sẽ chở được
\(M\) sẽ chở được ![]() \(20x\) người và
\(20x\) người và ![]() \(0,8x\) tấn hàng;
\(0,8x\) tấn hàng; ![]() \(y\) xe loại
\(y\) xe loại ![]() \(N\) sẽ chở được
\(N\) sẽ chở được ![]() \(10y\) người và
\(10y\) người và ![]() \(2y\) tấn hàng.
\(2y\) tấn hàng.
=> ![]() \(x\) xe loại
\(x\) xe loại ![]() \(M\) và
\(M\) và ![]() \(y\) xe loại
\(y\) xe loại ![]() \(N\) sẽ chở được
\(N\) sẽ chở được ![]() \(20x+10y\) người và
\(20x+10y\) người và ![]() \(0,8x+2y\) tấn hàng.
\(0,8x+2y\) tấn hàng.
Ta có hệ bất phương trình sau:
 \(\left\{ {\begin{array}{*{20}{c}} {20x + 10y \geqslant 150} \\ {0,8x + 2y \geqslant 10} \\ {0 \leqslant x \leqslant 10} \\ {0 \leqslant y \leqslant 9} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {2x + y \geqslant 15} \\ {2x + 5y \geqslant 25} \\ {0 \leqslant x \leqslant 10} \\ {0 \leqslant y \leqslant 9} \end{array}} \right. (*)\)
\(\left\{ {\begin{array}{*{20}{c}} {20x + 10y \geqslant 150} \\ {0,8x + 2y \geqslant 10} \\ {0 \leqslant x \leqslant 10} \\ {0 \leqslant y \leqslant 9} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {2x + y \geqslant 15} \\ {2x + 5y \geqslant 25} \\ {0 \leqslant x \leqslant 10} \\ {0 \leqslant y \leqslant 9} \end{array}} \right. (*)\)
Bài toán trở thành tìm giá trị nhỏ nhất của hàm số ![]() \(f(x;y)\) trên miền nghiệm của hệ (*).
\(f(x;y)\) trên miền nghiệm của hệ (*).
Miền nghiệm của hệ (*) là tứ giác ABCD (kể cả biên).
Hình vẽ minh họa

Hàm số ![]() \(f(x; y) = 4x+3y\) sẽ đạt giá trị nhỏ nhất trên miền nghiệm của hệ bất phương trình (*) khi
\(f(x; y) = 4x+3y\) sẽ đạt giá trị nhỏ nhất trên miền nghiệm của hệ bất phương trình (*) khi ![]() \((x;y)\) là tọa độ của một trong các đỉnh:
\((x;y)\) là tọa độ của một trong các đỉnh: ![]() \(A = \left( {\frac{{25}}{4};\frac{5}{2}} \right);B = \left( {10,1} \right);\)
\(A = \left( {\frac{{25}}{4};\frac{5}{2}} \right);B = \left( {10,1} \right);\) ![]() \(C = \left( {3,9} \right);D = \left( {10,9} \right)\)
\(C = \left( {3,9} \right);D = \left( {10,9} \right)\)
Ta có:  \(\left\{ \begin{gathered}
f\left( {\frac{{25}}{4};\frac{5}{2}} \right) = 32,5 \hfill \\
f\left( {10,1} \right) = 43 \hfill \\
f\left( {3,9} \right) = 39 \hfill \\
f\left( {10,9} \right) = 67 \hfill \\
\end{gathered} \right.\)
\(\left\{ \begin{gathered}
f\left( {\frac{{25}}{4};\frac{5}{2}} \right) = 32,5 \hfill \\
f\left( {10,1} \right) = 43 \hfill \\
f\left( {3,9} \right) = 39 \hfill \\
f\left( {10,9} \right) = 67 \hfill \\
\end{gathered} \right.\)
=> Giá trị của ![]() \(f(x;y)\) nhỏ nhất khi
\(f(x;y)\) nhỏ nhất khi ![]() \(\left( {x;y} \right) = \left( {3;9} \right)\). Như vậy để chi phí vận chuyển thấp nhất cần thuê 3 xe loại
\(\left( {x;y} \right) = \left( {3;9} \right)\). Như vậy để chi phí vận chuyển thấp nhất cần thuê 3 xe loại ![]() \(M\) và 9 xe loại
\(M\) và 9 xe loại ![]() \(N\).
\(N\).





