Mệnh đề nào sau đây đúng?
Cho ![]() là số tự nhiên, mệnh đề nào sau đây đúng?
là số tự nhiên, mệnh đề nào sau đây đúng?
Với thì
là hai số tự nhiên liên tiếp
là số chẵn
Với thì
là ba số tự nhiên liên tiếp
trong 3 số
có 1 số chia hết cho
Chọn đáp án là số chia hết cho
Đề kiểm tra 45 phút Toán 10 Chương 1 Mệnh đề và tập hợp sách Chân trời sáng tạo giúp bạn học tổng hợp lại kiến thức của cả nội dung chương. Cùng nhau luyện tập nha!
Mệnh đề nào sau đây đúng?
Cho ![]() là số tự nhiên, mệnh đề nào sau đây đúng?
là số tự nhiên, mệnh đề nào sau đây đúng?
Với thì
là hai số tự nhiên liên tiếp
là số chẵn
Với thì
là ba số tự nhiên liên tiếp
trong 3 số
có 1 số chia hết cho
Chọn đáp án là số chia hết cho
Chọn đáp án đúng
Mệnh đề nào sau đây là mệnh đề tương đương?
Mệnh đề tương đương là: “Hình thang nội tiếp đường tròn khi và chỉ khi nó là hình thang cân”.
Tìm mệnh đề sai
Cho tập hợp ![]() . Tìm mệnh đề sai trong các mệnh đề sau?
. Tìm mệnh đề sai trong các mệnh đề sau?
Các đáp án ,
,
đúng. Đáp án “
” sai.
Xét tính đúng sai của mệnh đề
Cho mệnh đề chứa biến ![]() chia hết cho 4” với
chia hết cho 4” với ![]() là số nguyên. Xét xem các mệnh đề
là số nguyên. Xét xem các mệnh đề ![]() và
và ![]() đúng hay sai?
đúng hay sai?
Thay và
vào
ta được các số
và
không chia hết cho
. Vậy
đúng và
sai.
Xét tính đúng sai của các mệnh đề
Cho các tập hợp ![]() ,
, ![]() và
và ![]() . Xét tính đúng sai của các mệnh đề sau:
. Xét tính đúng sai của các mệnh đề sau:
a) ![]() . Sai||Đúng
. Sai||Đúng
b) ![]() . Đúng||Sai
. Đúng||Sai
c) ![]() .Sai||Đúng
.Sai||Đúng
d) ![]() . Đúng||Sai
. Đúng||Sai
Cho các tập hợp ![]() ,
, ![]() và
và ![]() . Xét tính đúng sai của các mệnh đề sau:
. Xét tính đúng sai của các mệnh đề sau:
a) ![]() . Sai||Đúng
. Sai||Đúng
b) ![]() . Đúng||Sai
. Đúng||Sai
c) ![]() .Sai||Đúng
.Sai||Đúng
d) ![]() . Đúng||Sai
. Đúng||Sai
a) Sai:.
b) Đúng:.
c) Sai:.
d) Đúng: .
Chọn đáp án không thích hợp
Câu nào sau đây không là mệnh đề?
Vì “Bạn học giỏi quá!” là câu cảm thán không có khẳng định đúng hoặc sai.
Tìm câu sai
Cho ![]() ,
, ![]() ,
, ![]() . Chọn phát biểu sai.
. Chọn phát biểu sai.
Ta có:
Vậy câu sai là:
Tìm m để hai tập khác tập rỗng
Cho hai tập hợp khác rỗng ![]() và
và ![]() với
với ![]() . Tìm
. Tìm ![]() để
để ![]() .
.
Ta có
Từ (*) và (**) suy ra .
Chọn đáp án chính xác
Viết mệnh đề sau bằng cách sử dụng kí hiệu ![]() hoặc
hoặc ![]() : “Có một số nguyên bằng bình phương của chính nó”.
: “Có một số nguyên bằng bình phương của chính nó”.
Đáp án cần tìm là: .
Trong các mệnh đề sau, mệnh đề nào đúng?
Trong các mệnh đề sau, mệnh đề nào đúng?
Xét mệnh đề không chia hết cho 3:
TH1: với
, ta có:
không chia hết cho
TH2: với
, ta có:
không chia hết cho
TH3: với
, ta có:
không chia hết cho
thì
không chia hết cho
Tìm mệnh đề đảo đúng
Mệnh đề nào sau đây có mệnh đề đảo đúng?
Nếu một phương trình bậc hai có thì phương trình đó vô nghiệm.
Tìm tham số m thỏa mãn điều kiện
Cho hai tập hợp ![]() ,
, ![]() . Tìm m để
. Tìm m để ![]() .
.
Biểu diễn tập hợp trên trục số
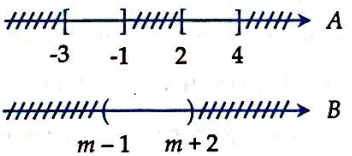
Ta đi tìm m để
hay
Tìm mệnh đề sai trong các mệnh đề sau
Cho 2 mệnh đề: “Quyển vở này của Nam” và “Quyển vở này có 118 trang”.
Cho biết 2 mệnh đề trên đều đúng, tìm mệnh đề sai trong các mệnh đề sau:
Đặt “Quyển vở này của Nam”,
“Quyển vở này có 118 trang”
Theo đề bài, đúng,
đúng nên
sai,
sai.
Mệnh đề chỉ sai khi
đúng
sai.
Chọn đáp án Quyển vở này của Nam nên nó không có 118 trang.
Xét tính đúng, sai của hai mệnh đề A và B.
Cho hai mệnh đề A: “∀ x ∈ R: ![]() ” và B: “∃ n ∈ Z:
” và B: “∃ n ∈ Z: ![]() ”. Xét tính đúng, sai của hai mệnh đề A và B.
”. Xét tính đúng, sai của hai mệnh đề A và B.
Với mệnh đề A, thay nên A sai.
Với mệnh đề B, thay nên B đúng.
Xác định hợp của ba tập hợp
Cho ba tập hợp ![]()
![]()
![]() khi đó tập
khi đó tập ![]() là:
là:
Giải phương trình mà
nên
Giải bất phương trình . Mà
nên chọn
Giải phương trình mà
nên
Giải bất phương trình
Tìm mệnh đề sai
Trong các mệnh đề sau, mệnh đề nào sai?
Xét mệnh đề thì
.
Chọn
thì
là mệnh đề sai.
Tìm số tập X thỏa mãn điều kiện
Cho tập ![]() ,
, ![]() . Có bao nhiêu tập
. Có bao nhiêu tập ![]() thỏa mãn
thỏa mãn ![]() ?
?
Các tập thỏa mãn là
,
,
,
.
Chọn phương án thích hợp
Cho hai tập hợp ![]() thỏa mãn
thỏa mãn ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
Biểu đồ Ven:
Vậy đáp án cần tìm là:
Phát biểu mệnh đề
Mệnh đề ![]() khẳng định rằng:
khẳng định rằng:
Mệnh đề khẳng định rằng: “Có ít nhất một số thực mà bình phương của nó bằng 5.”
Tìm câu không phải mệnh đề
Câu nào trong các câu sau không phải là mệnh đề?
Xét đáp án: là một câu khẳng định đúng nên là mệnh đề.
Xét đáp án: là một số vô tỷ nên B là một câu khẳng định sai vậy là mệnh đề.
Xét đáp án: là một câu khẳng định sai vậy là mệnh đề.
Xét đáp án “ có phải là một số hữu tỷ không?”: Đây là câu hỏi nên không phải là mệnh đề.
Xác định số tập hợp của phần tử
Cho hai tập hợp ![]() và
và ![]() . Tập hợp
. Tập hợp ![]() có bao nhiêu phần tử?
có bao nhiêu phần tử?
Ta có . Do đó
có
phần tử.
Tìm hợp của hai tập hợp
Cho ![]() và
và ![]() Khi đó,
Khi đó, ![]() là:
là:
Vậy
Chọn mệnh đề đúng
Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
Mệnh đề đúng là: “”.
Chọn đáp án đúng
Cho ![]() ,
, ![]() ,
, ![]() . Tập
. Tập ![]() có bao nhiêu phần tử là số nguyên.
có bao nhiêu phần tử là số nguyên.
Ta có : có
phần tử là số nguyên.
Tìm hiệu hai tập hợp
Cho A = {1; 3; 4; 7} và B = {3; 5; 7; 10} . Tập A\ B là:
Ta có: A\ B = {1; 4}.
Xác định mệnh đề sai
Phát biểu nào sau đây là sai?
Câu sai là: Không thể phát biểu mệnh đề: "Nếu tập A có n phần tử thì tập A có 2 tập con" dưới dạng điều kiện cần, điều kiện đủ
Chọn đáp án đúng
Cho ![]() ,
, ![]() và
và ![]() . Khi đó,
. Khi đó, ![]() là:
là:
Ta có:
Suy ra
Xác định số tập hợp X
Cho hai tập hợp ![]() và
và ![]() . Số tập hợp X thỏa mãn
. Số tập hợp X thỏa mãn ![]() là:
là:
Ta có có 3 phần tử nên số tập con
có
(tập).
Tìm mệnh đề sai
Trong các mệnh đề sau, mệnh đề nào sai?
Xét mệnh đề . Ta thấy
sai nên mệnh đề này sai.
Tìm mệnh đề đảo
Cho mệnh đề: “Nếu 2 góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh đề sau đây, đâu là mệnh đề đảo của mệnh đề trên?
Đáp án cần tìm là: “Nếu 2 góc bằng nhau thì hai góc đó ở vị trí so le trong”.
Tìm A\B
Cho hai tập hợp ![]() khi đó tập
khi đó tập ![]() là
là
Ta tìm tất cả các phần tử mà tập có mà tập
không có.
Vậy đáp án cần tìm là:
Tìm tất cả các tập con của tập A
Cho tập hợp ![]() khi đó tập hợp A có tất cả bao nhiêu tập con.
khi đó tập hợp A có tất cả bao nhiêu tập con.
Cách 1: Liệt kê các tập con của tập là
do đó chọn đáp án là 8.
Cách 2: Số tất cả các tập con của tập có
phần tử có công thức
Do đó dùng máy tính ấn
Định tham số m thỏa mãn điều kiện
Cho 3 tập hợp ![]() ,
, ![]() ,
, ![]() . Tìm m để
. Tìm m để ![]() .
.
Biểu diễn tập hợp trên trục số

Ta đi tìm m để
- TH1: Nếu thì
- TH2: Nếu
Vì nên

Mệnh đề nào sau đây sai?
Biết A là mệnh đề đúng, B là mệnh đề sai, C là mệnh đề đúng. Mệnh đề nào sau đây sai?
Ta có: là mệnh đề đúng,
là mệnh đề sai nên
là mệnh đề sai.
là mệnh đề đúng,
là mệnh đề sai nên
là mệnh đề sai.
Chọn đáp án
Chọn đáp án đúng
Cho tập hợp ![]() và
và ![]() . Có bao nhiêu tập
. Có bao nhiêu tập ![]() thỏa mãn
thỏa mãn ![]() ?
?
Có 4 tập hợp thỏa mãn
là:
;
;
và
.
Xác định số phần tử nguyên của X
Cho hai tập hợp ![]() ,
, ![]() thỏa mãn
thỏa mãn ![]() và
và ![]() . Xác định số phần tử là số nguyên của
. Xác định số phần tử là số nguyên của ![]() .
.
Do .
Mà .
Suy ra .
Vậy số phần tử nguyên của tập là
.
Chọn đáp án thích hợp
Khẳng định nào sau đây là mệnh đề?
Đáp án cần tìm là: “Sao hỏa không thuộc hệ thái dương”.
Tìm mệnh đề phủ định
Cho mệnh đề P: “∀ x ∈ R: |x| ≥ 0” . Phủ định của mệnh đề P là:
Phủ định của mệnh đề P là: “∃ x ∈ R: |x| < 0”.
Chọn đáp án đúng
Cho hai tập hợp ![]() . Tìm giá trị của a để
. Tìm giá trị của a để ![]() .
.
Để khi và chỉ khi
.
Vậy là giá trị cần tìm.
Chọn phương án chính xác
Cho hai tập hợp ![]() . Tập nào sau đây bằng tập
. Tập nào sau đây bằng tập ![]() ?
?
Vì gồm các phần tử vừa thuộc
vừa thuộc
.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
