Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 10 Khóa học Lớp 10 Toán 10 - Chân trời sáng tạo

Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 3

Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ
Mô tả thêm:

Cùng nhau ôn tập, thử sức với Đề thi HK2 Toán lớp 10 - Chân trời sáng tạo nha!
  • Thời gian làm: 90 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Bắt đầu làm bài
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
  • Câu 1: Thông hiểu

    Viết phương trình chính tắc của (P)

    Hãy xác định phương trình chính tắc của parabol (P). Biết rằng (P) cắt đường thẳng d:x + 2y = 0 tại hai điểm A,B và AB = 4\sqrt{5}?

    Phương trình chính tắc của (P) có dạng y^{2} = 2px;(p > 0)

    Ta có đường thẳng d cắt (P) tại hai điểm \left\{ \begin{matrix} A \equiv O \\ B = ( - 2m;m) \\ \end{matrix} ight.

    Ta có:

    AB = 4\sqrt{5} \Leftrightarrow AB^{2} = 5m^{2} = \left( 4\sqrt{5} ight)^{2}

    \Leftrightarrow m^{2} = 16 \Leftrightarrow m = \pm 4

    Với m = 4 \Rightarrow B( - 8;4) \Rightarrow 16 = 2p.( - 8) \Rightarrow p = - 1 < 0(ktm)

    Với m = - 4 \Rightarrow B(8; - 4) \Rightarrow 16 = 2p.8 \Rightarrow p = 1(tm)

    Vậy phương trình chính tắc của parabol cần tìm là: y^{2} = 2x.

  • Câu 2: Nhận biết

    Tìm điều kiện chính xác

    Cho f(x)=ax^{2}+bx+c(a≠0). Điều kiện để f(x)>0 \forall x \in \mathbb{R} là:

     Ta có: f(x)=ax^{2}+bx+c>0 \forall x \in \mathbb{R} \Leftrightarrow\left\{\begin{matrix}a>0\\ \Delta < 0\end{matrix}ight..

  • Câu 3: Nhận biết

    Tìm tiêu điểm của Hypebol

    Đường Hyperbol \frac{x^{2}}{16} - \frac{y^{2}}{9} = 1 có một tiêu điểm là điểm nào dưới đây?

    Ta có : \left\{ \begin{matrix} a^{2} = 16 \\ b^{2} = 9 \\ c^{2} = a^{2} + b^{2} \\ \end{matrix} ight.\ \Rightarrow c = 5. Các tiêu điểm của (H) là ( - 5;0) và (5;0).

  • Câu 4: Nhận biết

    Tính giá trị biểu thức

    Giá trị của C_{n}^{0}-C_{n}^{1}+C_{n}^{n-1}-C_{n}^{n} bằng:

    Ta có:

    \begin{matrix} C_n^0 - C_n^1 + C_n^{n - 1} - C_n^n \hfill \\ = 1 - C_n^1 + C_n^1 - 1 = 0 \hfill \\ \end{matrix}

  • Câu 5: Thông hiểu

    Hỏi có bao nhiêu cách sắp xếp

    Xếp 6 chữ số 1, 1, 2, 2, 3, 4 thành hàng ngang sao cho hai chữ số giống nhau thì không xếp cạnh nhau. Hỏi có bao nhiêu cách sắp xếp như vậy?

    Số cách xếp sáu chữ số thành hàng một cách tùy ý là \frac{6!}{2!.2!} = 180.

    *) Tìm số cách xếp sáu chữ số sao cho có hai chữ số giống nhau đứng cạnh nhau

    +) TH1: Số cách xếp sao cho có hai chữ số 1 đứng cạnh nhau 5.\frac{4!}{2!} = 60.

    +) TH2: Số cách xếp sao cho có hai chữ số 2 đứng cạnh nhau 5.\frac{4!}{2!} = 60.

    +) TH3: Số cách xếp sao cho có hai chữ số 1 đứng cạnh nhau và hai chữ số 2 đứng cạnh nhau

    -) Nếu hai chữ số 1 ở vị trí (1;2)và (5;6) ta có số cách xếp là 2.3.2 = 12.

    -) Nếu hai chữ số 1 ở ba vị trí còn lại thì số các xếp là 3.2.2 =12.

    Vậy số cách xếp hai chữ số giống nhau đứng cạnh nhau là 60 + 60 - 12 - 12 = 96.

    \Rightarrow Số cách xếp không có hai chữ số giống nhau nào đứng cạnh nhau là 180 - 96 = 84.

  • Câu 6: Nhận biết

    Tam thức bậc hai nhận giá trị không âm khi và chỉ khi

    Tam thức bậc hai f(x) =  − x2 + 3x − 2 nhận giá trị không âm khi và chỉ khi

    f(x) = - x^{2} + 3x - 2 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = 2 \\ \end{matrix} ight.

    Dựa vào bảng xét dấu, ta chọn đáp án x ∈ [1; 2].

  • Câu 7: Vận dụng

    Tính xác suất để hai số đều chia hết cho 3

    Cho tập hợp M = \left\{ 1;2;3;4;5 ight\}. Gọi S là tập hợp các số tự nhiên có 3 chữ đôi một khác nhau được lập thành từ các chữ số thuộc tập M. Chọn ngẫu nhiên hai số từ tập S, tính xác suất để hai số được chọn đều chia hết cho 3?

    Gọi B là biến cố chọn được hai số đều chia hết cho 3

    Số các số tự nhiên có 3 chữ số được lập thành từ tập M là: A_{5}^{3} = 60

    Khi đó số phần tử của không gian mẫu là: n(\Omega) = C_{60}^{2}

    Tập các số gồm 3 chữ số tạo thành các số chia hết cho 3 là:

    \left\{ (1;2;3),(1;3;5),(2;3;4) ight\}

    Mỗi tập trên tạo thành 3! số chia hết cho 3 nên ta có: 3.3! = 18 số chia hết cho 3

    Khi đó n(B) = C_{18}^{2}

    Vậy xác suất để chọn được hai số đều chia hết cho 3 từ tập S là: p(B) = \frac{n(B)}{n(\Omega)} = \frac{C_{18}^{2}}{C_{60}^{2}} = \frac{51}{590}

  • Câu 8: Nhận biết

    Tìm tâm và bán kính đường tròn

    Xác định tâm và bán kính đường tròn (C):(x - 4)^{2} + (y + 5)^{2} = 12?

    Ta có: (C):(x - 4)^{2} + (y + 5)^{2} = 12

    Vậy đường tròn có bán kính I(4; - 5) và bán kính R = 2\sqrt{3}

  • Câu 9: Thông hiểu

    Xác định phương trình đường tròn

    Viết phương trình đường tròn (C) có tâm I( - 1;2) và tiếp xúc với đường thẳng \Delta:x - 2y + 7 = 0?

    Bán kính đường tròn là khoảng cách từ tâm I đến đường thẳng \Delta:x - 2y + 7 = 0 nên

    R = d(I;\Delta) = \frac{| - 1 - 4 - 7|}{\sqrt{1 + 4}} = \frac{2}{\sqrt{5}}

    Vậy phương trình đường tròn cần tìm là: (x + 1)^{2} + (y - 2)^{2} = \frac{4}{5}.

  • Câu 10: Nhận biết

    Chọn phương trình chính tắc của Parabol

    Trong các phương trình sau đây, phương trình nào là phương trình chính tắc của Parabol?

    Phương trình Parabol có dạng y^{2} = 2px

    Vậy phương trình cần tìm là y^{2} = 2x.

  • Câu 11: Thông hiểu

    Chọn khẳng định đúng

    Cho hàm số y = f(x) = ax2 + bx + c có đồ thị như hình vẽ. Đặt Δ = b2 − 4ac, tìm dấu của a và Δ.

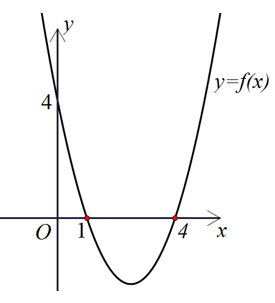
    Nhìn đồ thị, ta thấy đồ thị y = f(x) cắt trục hoành tại 2 điểm x = 1, x = 4 nên Δ > 0, dựa vào hình dạng parabol nên suy a > 0

  • Câu 12: Nhận biết

    Viết khai triển theo công thức nhị thức Niu-tơn

    Viết khai triển theo công thức nhị thức Niu-tơn (x - y)^{5}.

    Ta có:

    (x - y)^{5} = \left\lbrack x + ( - y) ightbrack^{5}

    = C_5^0{x^5} + C_5^1{x^4}{\left( { - y} ight)^1} + C_5^2{x^3}{\left( { - y} ight)^2} + C_5^3{x^2}{\left( { - y} ight)^3} + C_5^4{x^1}{\left( { - y} ight)^4} + C_5^5{\left( { - y} ight)^5}

    Hay (x - y)^{5} = x^{5} - 5x^{4}y + 10x^{3}y^{2} - 10x^{2}y^{3} + 5xy^{4} - y^{5}.

  • Câu 13: Thông hiểu

    Tìm phương trình nội tiếp tam giác

    Cho tọa độ hai điểm A(8;0),B(0;6). Phương trình đường tròn ngoại tiếp tam giác OAB là:

    Ta có tam giác OAB vuông tại O nên tâm I của đường tròn ngoại tiếp tam giác là trung điểm của cạnh huyền AB suy ra I(4; 3) và bán kính R = IA = \sqrt{(8 - 4)^{2} + (0 - 3)^{2}} = 5

    Vậy phương trình đường tròn ngoại tiếp tam giác OAB là: (x - 4)^{2} + (y - 3)^{2} = 25

  • Câu 14: Thông hiểu

    Hỏi bài thi đó có tất cả bao nhiêu đáp án?

    Một bài thi trắc nghiệm khách quan gồm 8 câu hỏi. Mỗi câu hỏi gồm 4 đáp án trả lời. Hỏi bài thi đó có tất cả bao nhiêu đáp án?

    Mỗi câu hỏi gồm 4 đáp án, có 8 câu hỏi nên có: 4.4.4.4.4.4.4.4 = 4^{8} (đáp án). (quy tắc nhân)

  • Câu 15: Thông hiểu

    Tìm tọa độ điểm D

    Trong mặt phẳng tọa độ Oxy, cho ba điểm A( - 1;2),B(2; - 2),C(3;1). Biết rằng \overrightarrow{AD} = \overrightarrow{BC}, khi đó tọa độ điểm D là:

    Giả sử tọa độ điểm D = (x;y)

    Ta có: \left\{ \begin{matrix} \overrightarrow{AD} = (x + 1;y - 2) \\ \overrightarrow{BC} = (1;3) \\ \end{matrix} ight.

    Vì \overrightarrow{AD} = \overrightarrow{BC} nên \left\{ \begin{matrix} x + 1 = 1 \\ y - 2 = 3 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x = 0 \\ y = 5 \\ \end{matrix} ight.\ \Leftrightarrow D(0;5)

  • Câu 16: Nhận biết

    Tìm số hạng thỏa mãn

    Số hạng chứa x^{34} trong khai triển \left( x + \frac{1}{x} ight)^{40} là:

    Số hạng thứ k + 1 trong khai triển \left( x + \frac{1}{x} ight)^{40} là:

    a_{k + 1} = C_{40}^{k}x^{40 - k}.\left( \frac{1}{x} ight)^{k} = C_{40}^{k}x^{40 - k}x^{- k} = C_{40}^{k}x^{40 - 2k}.

    Số hạng chứa x^{34} trong khai triển \left( x + \frac{1}{x} ight)^{40} tương ứng với: 40 - 2k = 34 \Leftrightarrow k = 3.

    Vậy số hạng chứa x^{34} trong khai triển \left( x + \frac{1}{x} ight)^{40} là: C_{40}^{3}x^{34}.

  • Câu 17: Vận dụng

    Xác định phương trình đường thẳng BC

    Cho tam giác ABC có phương trình các cạnh AB;AC lần lượt là 5x - 2y + 6 = 0,4x + 7y - 21 = 0 và trực tâm H(1;1). Phương trình tổng quát của cạnh BC là:

    Ta có: A = AB \cap AC nên tọa độ điểm A là nghiệm hệ phương trình:

    \left\{ \begin{matrix} 5x - 2y + 6 = 0 \\ 4x + 7y - 21 = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x = 0 \\ y = 3 \\ \end{matrix} ight.

    \Rightarrow A(0;3) \Rightarrow \overrightarrow{AH} = (1; - 2)

    Ta có BH\bot AC \Rightarrow BH:7x - 4y + a = 0

    Điểm H \in BH \Leftrightarrow 7 - 4 + a = 0 \Leftrightarrow a = - 3

    \Rightarrow BH:7x - 4y - 3 = 0

    Ta có: B = AB \cap BH nên tọa độ điểm B là nghiệm hệ phương trình:

    \left\{ \begin{matrix}5x - 2y + 6 = 0 \\7x - 4y - 3 = 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x = - 5 \\y = - \dfrac{19}{2} \\\end{matrix} ight.

    \Rightarrow B\left( - 5; - \frac{19}{2} ight)

    Đường thẳng BC đi qua điểm B nhận \overrightarrow{AH} làm vecto pháp tuyến có phương trình là:

    x + 5 - 2\left( x + \frac{19}{2} ight) = 0 \Leftrightarrow x - 2y - 14 = 0

  • Câu 18: Thông hiểu

    Tính giá trị biểu thức M

    Biến đổi biểu thức \left( 2 + \sqrt{3} ight)^{5} - \left( 2 - \sqrt{3} ight)^{4} dưới dạng a + b\sqrt{3};\left( a,b\mathbb{\in Z} ight). Tính giá trị biểu thức M = a - 2b + 500?

    Ta có:

    \left( 2 + \sqrt{3} ight)^{5} - \left( 2 - \sqrt{3} ight)^{4} = 265 - 265\sqrt{3}

    \Rightarrow \left\{ \begin{matrix} a = 265 \\ b = 265 \\ \end{matrix} ight.\ \Rightarrow M = 235

  • Câu 19: Nhận biết

    Tìm vectơ chỉ phương

    Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng \left\{\begin{matrix}x=2\\ y=-1+6t\end{matrix}ight.?

     Vectơ chỉ phương của đường thẳng trên là: (0;6) \Rightarrow \overrightarrow u = (0;1).

  • Câu 21: Vận dụng

    Tìm đường thẳng thỏa mãn

    Tập hợp các điểm cách đường thẳng \Delta:3x - 4y + 2 = 0 một khoảng bằng 2 là hai đường thẳng có phương trình nào sau đây?

    d\left( M(x;y);\Delta ight) = 2 \Leftrightarrow \frac{|3x - 4y + 2|}{5} = 2 \Leftrightarrow \left\lbrack \begin{matrix} 3x - 4y + 12 = 0 \\ 3x - 4y - 8 = 0 \\ \end{matrix} ight.\ .

  • Câu 22: Nhận biết

    Tìm tọa độ giao điểm của hai đường thẳng

    Tìm tọa độ giao điểm của hai đường thẳng 7x - 3y + 16 = 0 và x + 10 = 0.

    \left\{ \begin{matrix} d_{1}:7x - 3y + 16 = 0 \\ d_{2}:x + 10 = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x = - 10 \\ y = - 18 \\ \end{matrix} ight.\ . Chọn ( - 10; - 18).

  • Câu 23: Vận dụng cao

    Tìm điều kiện của m

    Tất cả các giá trị của tham số m để các nghiệm của phương trình \sqrt{x+1}-2=0\;(1) cũng là nghiệm của phương trình x2 − 2mx − m2 − 2 = 0 (2) là:

    \sqrt{x + 1} = 2 \Leftrightarrow x + 1 = 4 \Leftrightarrow x = 3

    Do đó, để mọi nghiệm của (1) cũng là nghiệm của (2) điều kiện là x = 3 cũng là nghiệm của (2), tức là: 9 - 6m - m^{2} - 2 = 0 \Leftrightarrow m^{2} + 6m - 7 = 0 \Leftrightarrow \left\lbrack \begin{matrix} m = 1 \\ m = - 7 \\ \end{matrix} ight..

  • Câu 24: Vận dụng

    Tìm tập xác định

    Tìm tập xác định D của hàm số f(x) = \sqrt{\sqrt{x^{2} + x - 12} - 2\sqrt{2}}.

    Hàm số xác định khi và chỉ khi \left\{ \begin{matrix} \sqrt{x^{2} + x - 12} - 2\sqrt{2} \geq 0 \\ x^{2} + x - 12 \geq 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} x^{2} + x - 12 \geq 8 \\ x^{2} + x - 12 \geq 0 \\ \end{matrix} \Leftrightarrow ight.\ x^{2} + x - 12 \geq 8

     ⇔ x2 + x − 20 ≥ 0

    Bảng xét dấu

    Dựa vào bảng xét dấu, ta thấy x2 + x − 20 ≥ 0 ⇔ x ∈ (−∞ ; −5) ∪ (4 ;  + ∞].

    Vậy tập xác định của hàm số là D = (−∞ ; −5) ∪ (4 ;  + ∞].

  • Câu 25: Nhận biết

    Tìm tập nghiệm của bất phương trình

    Tập nghiệm S của bất phương trình x^{2} + x - 12 < 0 là:

     Ta có: x^{2} + x - 12 < 0 \Leftrightarrow -4< x <3.

    Suy ra S = (-4;3).

  • Câu 26: Nhận biết

    Tìm điều kiện chính xác

    Cho phương trình x^{2} + y^{2} – 2ax – 2by + c = 0. Điều kiện của a, b, c để phương trình đã cho là phương trình đường tròn là

     Điều kiện: a^{2} + b^{2} > c.

  • Câu 27: Thông hiểu

    Tìm tập nghiệm S

    Tập nghiệm S của phương trình \sqrt{2x}+x-1=0 là:

     Ta có: \sqrt{2x}+x-1=0 \Rightarrow 2x=(1-x)^2\Leftrightarrow 2x=1-2x+x^2 \Leftrightarrow x^2-4x+1=0\Leftrightarrow x=2-\sqrt3.

    Vậy S =\{2-\sqrt{3}\}.

  • Câu 28: Nhận biết

    Phương trình có nghiệm là

    Phương trình \sqrt{x^{2} + 4x - 1} = x - 3 có nghiệm là bao nhiêu?

    \sqrt{x^{2} + 4x - 1} = x - 3\Leftrightarrow \left\{ \begin{matrix}x - 3 \geq 0 \\x^{2} + 4x - 1 = x^{2} - 6x + 9 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x \geq 3 \\x = 1\ \ (L) \\\end{matrix} ight..

    Vậy phương trình vô nghiệm.

  • Câu 29: Vận dụng cao

    Tính xác suất để con cóc đáp xuống điểm thỏa mãn yêu cầu

    Trên mặt phẳng tọa độ Oxy, ta xét một hình chữ nhật ABCD với các điểm A( - 2;0),B( - 2;2),C(4;2),D(4;0) (như hình vẽ):

    Một con cóc nhảy trong hình chữ nhật tính cả trên cạnh hình chữ nhật sao cho chân của nó luôn đáp xuống mặt phẳng tại các điểm có tọa độ nguyên (tức là điểm có cả hoành độ và tung độ đều nguyên). Tính xác suất để con cóc đáp xuống các điểm M(x;y) mà x + y < 2.

    Số các điểm có tọa độ nguyên thuộc hình chữ nhật là 7.3 = 21 điểm vì \left\{ \begin{matrix} x \in \left\{ - 2; - 1;0;1;2;3;4 ight\} \\ y \in \left\{ 0;1;2 ight\} \\ \end{matrix} ight.

    Để con có đáp xuống các điểm M(x;y) mà x + y < 2 thì con cóc sẽ nhảy trong khu vực hình thang BEIA. Để M(x;y) có tọa độ nguyên thì \left\{ \begin{matrix} x \in \left\{ - 2; - 1;0;1;2 ight\} \\ y \in \left\{ 0;1;2 ight\} \\ \end{matrix} ight.

    Nếu x \in \left\{ - 2; - 1 ight\} thì y \in \left\{ 0;1;2 ight\} suy ra có: 2.3 = 6 điểm

    Nếu x = 0 thì y \in \left\{ 0;1 ight\} suy ra có: 1.2 = 2 điểm

    Nếu x = 1 thì y = 0 suy ra có: 1 điểm

    Số kết quả thuận lợi cho biến cố: “Con cóc đáp xuống các điểm M(x;y) mà x + y < 2” là: 6 + 2 + 1 = 9

    Vậy xác suất của biến cố: “Con cóc đáp xuống các điểm M(x;y) mà x + y < 2” là: \frac{9}{21} = \frac{3}{7}.

  • Câu 30: Thông hiểu

    Tính khoảng cách từ điểm đến đường thẳng

    Khoảng cách từ điểm M(2;0) đến đường thẳng \Delta:\left\{ \begin{matrix} x = 1 + 3t \\ y = 2 + 4t \\ \end{matrix} ight. bằng:

    \Delta:\left\{ \begin{matrix} x = 1 + 3t \\ y = 2 + 4t \\ \end{matrix} ight.\ ightarrow \Delta:4x - 3y + 2 = 0 ightarrow d(M;\Delta) = \frac{|8 + 0 + 2|}{\sqrt{16 + 9}} = 2.

  • Câu 31: Vận dụng

    Tìm tất cả các giá trị của m

    Trong mặt phẳng tọa độ Oxy cho đường tròn (C):x^{2} + y^{2} - 2x - 2my + m^{2} - 24 = 0 có tâm I và đường thẳng \Delta:mx + 4y = 0 (với m là tham số). Biết đường thẳng \Delta cắt đường tròn (C) tại hai điểm A;B phân biệt sao cho diện tích tam giác IAB bằng 12. Có bao nhiêu giá trị của tham số m thỏa mãn yêu cầu đề bài?

    Hình vẽ minh họa

    Đường tròn (C) có tâm I(1; m) và bán kính R = 5.

    Gọi H là trung điểm của dây cung AB. Ta có IH là đường cao của tam giác IAB và

    IH = d(I;\Delta) \Leftrightarrow \frac{|m + 4m|}{\sqrt{m^{2} + 16}} = \frac{|5m|}{\sqrt{m^{2} + 16}}

    AH = \sqrt{IA^{2} - IH^{2}} = \sqrt{25 - \frac{(5m)^{2}}{m^{2} + 16}} = \frac{20}{\sqrt{m^{2} + 16}}

    Theo bài ra ta có:

    S_{IAB} = 12 \Leftrightarrow 2S_{IAH} = 12

    \Leftrightarrow d(I;\Delta).AH = 12

    \Leftrightarrow 25|m| = 3\left( m^{2} + 16 ight)

    \Leftrightarrow \left\lbrack\begin{matrix}m = \pm 3 \\m = \pm \dfrac{16}{3} \\\end{matrix} ight.

    Vậy có 4 giá trị của tham số m thỏa mãn yêu cầu bài toán.

  • Câu 32: Thông hiểu

    Tìm hai đường thẳng thỏa mãn

    Góc tạo bởi hai đường thẳng nào dưới đây bằng 90°.

     Xét hai đường thẳng d_1: 6x – 5y + 4 = 0 và d_2:\left\{\begin{matrix}x=10-6t\\ y=1+5t\end{matrix}ight..

    Ta có: \overrightarrow {{n_1}} = (6; - 5);\overrightarrow {{n_2}} = (5;6). 

    Mà \overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 6.5 - 5.6 = 0 nên suy ra hai đường thẳng vuông góc với nhau.

  • Câu 33: Thông hiểu

    Xác suất để tổng hai số là một số chẵn

    Chọn ngẫu nhiên hai số khác nhau từ 30 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn bằng:

    Số phần tử không gian mẫu là: n(\Omega) = C_{30}^{2} = 435

    Gọi A là biến cố: “Hai số được chọn có tổng là một số chẵn”

    Tổng của hai số là một số chẵn khi và chỉ khi hai số đó đều chẵn hoặc đều lẻ.

    Trong 30 số nguyên dương đầu tiên có 15 số lẻ và 15 số chẵn.

    Xét trường hợp chọn được hai số lẻ ta có: C_{15}^{2} cách chọn.

    Xét trường hợp chọn được hai số chẵn ta có: C_{15}^{2} cách chọn.

    Suy ra số kết quả thuận lợi cho biến cố A là: C_{15}^{2} + C_{15}^{2} = 210

    Khi đó xác suất của biến cố A là: P(A) = \frac{n(A)}{n(\Omega)} = \frac{210}{435} = \frac{14}{29}.

  • Câu 34: Thông hiểu

    Chọn đáp án đúng

    Cho bất phương trình x^{2}−8x+7≥0 . Trong các tập hợp sau đây, tập nào có chứa phần tử không phải là nghiệm của bất phương trình.

     Ta có: x^{2}−8x+7≥0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x \le 1}\\{x \ge 7}\end{array}} ight.. Suy ra S=[-\infty;1) \cup [7;+\infty).

    Nhận xét: [6;+\infty) không thuộc S.

  • Câu 35: Nhận biết

    Điền cụm từ vào chỗ trống

    Nguyên lí xác suất bé được phát biểu như sau: “Nếu có một biến cố có xác suất rất bé thì trong một phép thử biến cố đó sẽ …”. Cụm từ cần điền vào chỗ trống là:

    Nguyên lí xác suất bé được phát biểu như sau: “Nếu có một biến cố có xác suất rất bé thì trong một phép thử biến cố đó sẽ không xảy ra”.

  • Câu 36: Thông hiểu

    Chọn kết quả đúng

    Từ các số 1,2,3,4,5,6 có thể lập được bao nhiêu số tự nhiên có ba chữ số khác nhau?

    Mỗi số tự nhiên có ba chữ số khác nhau được lập từ các số 1,2,3,4,5,6 là một chỉnh hợp chập 3 của 6 phần tử.

    Vậy từ các số 1,2,3,4,5,6 có thể lập được: A_{6}^{3} = 120 số tự nhiên có ba chữ số khác nhau.

  • Câu 37: Vận dụng

    Có bao nhiêu số hạng là số nguyên trong khai triển

    Có bao nhiêu số hạng là số nguyên trong khai triển của biểu thức \left( \sqrt[3]{3} + \sqrt[5]{5} ight)^{2019}?

    Ta có \left( \sqrt[3]{3} + \sqrt[5]{5} ight)^{2019} = \sum_{k = 0}^{2019}{C_{2019}^{k}.\left( \sqrt[3]{3} ight)^{2019 - k}.\left( \sqrt[5]{5} ight)^{k}} = \sum_{k = 0}^{2019}{C_{2019}^{k}.3^{\frac{2019 - k}{3}}.5^{\frac{k}{5}}}.

    Để trong khai triển có số hạng là số nguyên thì \left\{ \begin{matrix} k\mathbb{\in N} \\ 0 \leq k \leq 2019 \\ \frac{2019 - k}{3}\mathbb{\in N} \\ \frac{k}{5}\mathbb{\in N} \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} k\mathbb{\in N} \\ 0 \leq k \leq 2019 \\ 673 - \frac{k}{3}\mathbb{\in N} \\ \frac{k}{5}\mathbb{\in N} \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} k\mathbb{\in N} \\ 0 \leq k \leq 2019 \\ k \vdots 15 \\ \end{matrix} ight..

    Ta có k \vdots 15 \Rightarrow k = 15m mà 0 \leq k \leq 2019 \Leftrightarrow 0 \leq 15m \leq 2019 \Leftrightarrow 0 \leq m \leq 134,6. Suy ra có 135 số hạng là số nguyên trong khai triển của biểu thức.

  • Câu 38: Thông hiểu

    Tìm n

    Trong khai triển \left( 3x^{2} + \frac{1}{x} ight)^{n}biết hệ số của x^{3} là 3^{4}C_{n}^{5}. Giá trị n có thể nhận là:

    Ta có \left( 3x^{2} + \frac{1}{x} ight)^{n} = \sum_{k = 0}^{n}{C_{n}^{k}\left( 3x^{2} ight)^{n - k}\left( \frac{1}{x} ight)^{k}} = \sum_{k = 0}^{n}{C_{n}^{k}3^{n - k}x^{2n - 3k}}.

    Biết hệ số của x^{3} là 3^{4}C_{n}^{5} nên \left\{ \begin{matrix} 2n - 3k = 3 \\ n - k = 4 \\ k = 5 \\ 0 \leq k \leq n,(k,n \in N) \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} k = 5 \\ n = 9 \\ \end{matrix} ight..

  • Câu 39: Nhận biết

    Tìm điểm thuộc đường thẳng

    Điểm nào sau đây thuộc đường thẳng d:\left\{ \begin{matrix} x = 1 + 2t \\ y = 3 - t \\ \end{matrix} ight. ?

    M(2;–1)\overset{x = 2,\ y = - 1 ightarrow d}{ightarrow}\left\{ \begin{matrix} 2 = 1 + 2t \\ - 1 = 3 - t \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} t = \frac{1}{2} \\ t = 4 \\ \end{matrix} ight.\ \ \ (VN) ightarrow M\boxed{\in}d.

    N(–7;0)\overset{x = - 7,\ y = 0 ightarrow d}{ightarrow}\left\{ \begin{matrix} - 7 = 1 + 2t \\ 0 = 3 - t \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} t = - 4 \\ t = 3 \\ \end{matrix} ight.\ \ (VN) ightarrow N\boxed{\in}d.

    P(3;5)\overset{x = 3,\ y = 5 ightarrow d}{ightarrow}\left\{ \begin{matrix} 3 = 1 + 2t \\ 5 = 3 - t \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} t = 1 \\ t = - 2 \\ \end{matrix} ight.\ \ (VN) ightarrow P\boxed{\in}d.

    Q(3;\ 2)\overset{x = 3,\ y = 2 \in d}{ightarrow}\left\{ \begin{matrix} 3 = 1 + 2t \\ 2 = 3 - t \\ \end{matrix} ight.\ \Leftrightarrow t = 1 ightarrow Q \in d.Chọn Q(3;\ 2).

  • Câu 40: Nhận biết

    Xét vị trí tương đối của hai đường thẳng

    Xét vị trí tương đối của hai đường thẳng d_{1}:\left\{ \begin{matrix} x = 4 + 2t \\ y = 1 - 5t \\ \end{matrix} ight. và d_{2}:5x + 2y - 14 = 0.

    \left. \ \begin{matrix} d_{1}:\left\{ \begin{matrix} x = 4 + 2t \\ y = 1 - 5t \\ \end{matrix} ight.\ ightarrow A(4;1) \in d_{1},\ \ {\overrightarrow{u}}_{1} = (2; - 5) \\ d_{2}:5x + 2y - 14 = 0 ightarrow \ \ {\overrightarrow{n}}_{2} = (5;2) ightarrow {\overrightarrow{u}}_{2} = (2; - 5) \\ \end{matrix} ight\} ightarrow \left\{ \begin{matrix} {\overrightarrow{u}}_{1} = {\overrightarrow{u}}_{2} \\ A\boxed{\in}d_{2} \\ \end{matrix} ight.\ ightarrow d_{1}||d_{2}.Chọn

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 3 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
  • Điểm thưởng: 0
Xem đáp án Làm lại
1
14 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 3
Thời gian còn lại 90:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Tìm bài trong mục này
🖼️

Toán 10 - Chân trời sáng tạo
Xem thêm