Hệ hai phương trình bậc nhất hai ẩn
Chuyên đề Toán học lớp 9: Hệ hai phương trình bậc nhất hai ẩn được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 9 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Hệ hai phương trình bậc nhất hai ẩn
I. KHÁI NIỆM VỀ HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Cho hai phương trình bậc nhất hai ẩn là ax + by = c và a'x + b' = c'. Khi đó ta có hệ phương trình bậc nhất hai ẩn là:
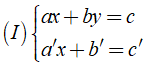
+ Nếu hai phương trình có nghiệm chung là (x0; y0) thì (x0; y0) được gọi là một nghiệm của hệ phương trình (I).
+ Nếu hai phương trình không có nghiệm chung thì hệ phương trình (I) vô nghiệm.
+ Giải hệ phương trình là tìm tất cả các nghiệm của nó.
II. MINH HỌA HÌNH HỌC TẬP NGHIỆM CỦA HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Cho hai phương trình bậc nhất hai ẩn là ax + by = c và a'x + b' = c'. Khi đó ta có hệ phương trình bậc nhất hai ẩn là:
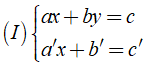
Gọi (d) và (d') là đồ thị hàm số của 2 hàm số rút ra từ 2 phương trình bậc nhất hai ấn của (I).
Đối với hệ phương trình (I), ta có:
Nếu (d) cắt (d') thì hệ (I) có một nghiệm duy nhất.
Nếu (d) song song với (d') thì hệ (I) vô nghiệm.
Nếu (d) trùng với (d') thì hệ (I) có vô số nghiệm.
Ví dụ: Xét hệ phương trình 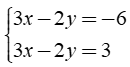
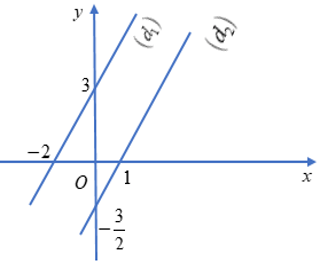
Do 3x - 2y = -6 ⇔ y = (3/2)x + 3 nên tập nghiệm của phương trình thứ nhất được biểu diễn bởi đường thẳng (d1): y = (3/2)x + 3.
Tương tự, tập nghiệm của phương trình thứ hai được biểu diễn bởi đường thẳng
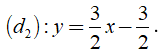
Hai đường thẳng (d1) và (d2) có tung độ gốc khác nhau và cùng hệ số góc là 3/2 nên song song với nhau, chung không có điểm chúng. Khi đó hệ đã cho vô nghiệm.
III. HỆ PHƯƠNG TRÌNH TƯƠNG ĐƯƠNG
Hai hệ phương trình được gọi là tương đương với nhau nếu chúng có cùng tập nghiệm.
Ta dùng kí hiệu "⇔" để chỉ sự tương đương của hai hệ phương trình.
Ví dụ: hai hệ phương trình tương đương là
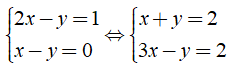
Bài lý thuyết: Hệ hai phương trình bậc nhất hai ẩn trên đây các bạn học sinh cùng quý thầy cô cần nắm vững kiến thức về khái niệm hệ phương trình bậc nhất hai ẩn, hệ phương trình tương đương...
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 9: Hệ hai phương trình bậc nhất hai ẩn. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 9, Giải bài tập Toán lớp 9 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc







