Biến đổi đơn giản biểu thức chứa căn thức bậc hai
Trong chương trình Toán học trung học cơ sở và trung học phổ thông, căn thức bậc hai là một phần kiến thức quan trọng và thường xuyên xuất hiện trong các bài kiểm tra, thi cử. Để giải các bài toán hiệu quả, việc biến đổi đơn giản biểu thức chứa căn thức bậc hai là kỹ năng cơ bản mà người học cần thành thạo. Bài viết này sẽ hướng dẫn bạn cách biến đổi căn thức sao cho biểu thức trở nên gọn gàng, dễ tính toán hơn, kèm theo ví dụ minh họa rõ ràng và dễ hiểu.
Chuyên đề: Biến đổi đơn giản biểu thức chứa căn thức bậc hai
I. Biến đổi biểu thức đơn giản chứa căn thức bậc hai
a) Đưa một thừa số ra ngoài dấu căn
Với hai biểu thức A, B mà B ≥ 0 ta có
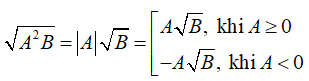
Ví dụ:
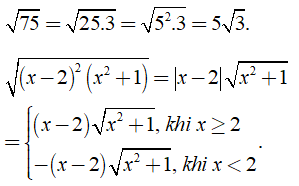
b) Đưa thừa số vào trong dấu căn
Với A ≥ 0, B ≥ 0 thì
Với A < 0, B ≥ 0 thì
Ví dụ:
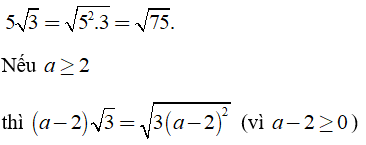
c) Khử mẫu của biểu thức dưới dấu căn
Với AB ≥ 0 và B ≠ 0 thì
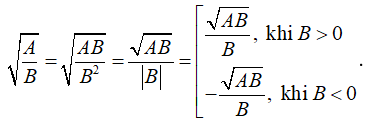
Ví dụ: 
\(\sqrt {\frac{7}{4}} = \sqrt {\frac{{7.4}}{{{4^2}}}} = \frac{{\sqrt {28} }}{4}\)
d) Trục căn thức ở mẫu
Trục căn thức ở mẫu số là biến đổi để biểu thức đó mất căn thức ở mẫu số
•Với các biểu thức A, B mà B > 0 ta có:
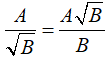
Ví dụ: \(\frac{2}{{\sqrt 3 }} = \frac{{2\sqrt 3 }}{3}\)
\(\frac{1}{{\sqrt {a + 2} }} = \frac{{\sqrt {a + 2} }}{{a + 2}};\left( {a > - 2} \right)\)
Với các biểu thức A, B, C mà A ≥ 0, A ≠ B2, ta có:
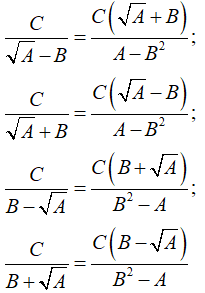
Ví dụ: \(\frac{5}{{\sqrt 3 + 2}} = \frac{{5\left( {\sqrt 3 - 2} \right)}}{{3 - 4}} = - 5\left( {\sqrt 3 - 2} \right)\)
Với các biểu thức A, B, C mà A ≥ 0, B ≥ 0, A ≠ B ta có:
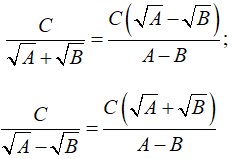
Ví dụ: \(\frac{2}{{\sqrt 3 + \sqrt 2 }} = \frac{{2\left( {\sqrt 3 - \sqrt 2 } \right)}}{{3 - 2}} = 2\left( {\sqrt 3 - \sqrt 2 } \right)\)
II. Rút gọn biểu thức chứa căn thức bậc hai
- Để rút gọn biểu thức chứa căn bậc hai, ta cần vận dụng phối hợp các phép tính và các phép biến đổi đã biết.
- Khi rút gọn một dãy các phép tính cộng, trừ, nhân, chia, lũy thừa và khai phương thì thứ tự thực hiện: khai căn trước rồi đến lũy thừa, sau đó đến nhân, chia, cộng, trừ
III. Bài tập trắc nghiệm có đáp án
Câu 1: Kết quả của biểu thức rút gọn C = √125 - 3√45 + 2√20?
| A. √5. | B. 0. | C. -√5. | D. 2√5. |
Hướng dẫn giải toán
Ta có:
\(C = \sqrt {125} - 3\sqrt {45} + 2\sqrt {20}\)
\(C = \sqrt {{5^2}.5} - 3\sqrt {{3^2}.5} + 2\sqrt {{2^2}.5}\)
\(C = 5\sqrt 5 - 9\sqrt 5 + 4\sqrt 5 = 0\)
Chọn đáp án B.
Câu 2: Kết quả so sánh nào sau đây đúng?
| A. \(2\sqrt 3 + \sqrt {27} > \sqrt {13}\) |
B. \(3\sqrt 5 > 4\sqrt 3\) |
| C. \(2\sqrt 6 = 6\sqrt {\frac{1}{2}}\) |
D. \(\frac{1}{3}\sqrt {15} < \frac{1}{4}\sqrt {20}\) |
Hướng dẫn giải toán
Ta có: \(2\sqrt 3 + \sqrt {27} = 2\sqrt 3 + 3\sqrt 3\) \(= 5\sqrt 3 = \sqrt {25.3} = \sqrt {75}\)
Mà \(75 > 13 \Rightarrow \sqrt {75} > \sqrt {13}\)
\(\Rightarrow 2\sqrt 3 + \sqrt {27} > \sqrt {13}\)
Chọn đáp án A.
Câu 3: Rút gọn biểu thức \(A = 2\sqrt a - a\sqrt{\frac{4}{a}} + {a^2}\sqrt {\frac{9}{{{a^3}}}}\) với a > 0?
| A. 3a | B. a√3 | C. 3√a | D. a/√3 |
Hướng dẫn giải toán
Khử mẫu của biểu thức dưới dấu căn
Ta có: \(A = 2\sqrt a - a\sqrt {\frac{4}{a}} + {a^2}\sqrt {\frac{9}{{{a^3}}}}\)
\(A = 2\sqrt a - \sqrt {\frac{{4{a^2}}}{a}} + \sqrt {\frac{{9{a^4}}}{{{a^3}}}}\)
\(A = 2\sqrt a - 2\sqrt a + 3\sqrt a = 3\sqrt a\)
Câu 4: Rút gọn biểu thức: \(P = \frac{1}{{\sqrt 2 - \sqrt 3 }} - \frac{1}{{\sqrt 3 - \sqrt 4 }} + \frac{1}{{\sqrt 4 - \sqrt 5 }} - ... + \frac{1}{{\sqrt {2n} - \sqrt {2n - 1} }}\)
| A. \(P = 1 - \sqrt {2n + 1}\) |
B.\(P = \sqrt {2n + 1} - \sqrt 2\) |
| C. \(P = - \left( {\sqrt 2 + \sqrt {2n + 1} } \right)\) |
D. \(P = \sqrt 2 + 1 + \sqrt {2n + 1}\) |
Hướng dẫn giải toán
Trục căn thức ở mẫu
Ta có: \(\frac{1}{{\sqrt a - \sqrt {a + 1} }} = \frac{{\sqrt a + \sqrt {a + 1} }}{{a - a - 1}} = - \left( {\sqrt a + \sqrt {a + 1} } \right)\)
Khi đó:
\(\frac{1}{{\sqrt 2 - \sqrt 3 }} = - \left( {\sqrt 2 + \sqrt 3 } \right)\)
...................................
\(\frac{1}{{\sqrt {2n} - \sqrt {2n + 1} }} = - \left( {\sqrt {2n} + \sqrt {2n + 1} } \right)\)
\(\begin{matrix}
\Rightarrow P = \dfrac{1}{{\sqrt 2 - \sqrt 3 }} - \dfrac{1}{{\sqrt 3 - \sqrt 4 }} + \dfrac{1}{{\sqrt 4 - \sqrt 5 }} - ... + \dfrac{1}{{\sqrt {2n} - \sqrt {2n - 1} }} \hfill \\
= - \left( {\sqrt 2 + \sqrt {2n + 1} } \right) \hfill \\
\end{matrix}\)
Chọn đáp án C.
Câu 5: Cho biểu thức:
\(A = \left( {1 - \frac{{a - 3\sqrt a }}{{a - 9}}} \right):\left( {\frac{{\sqrt a - 2}}{{\sqrt a + 3}} + \frac{{\sqrt a - 3}}{{2 - \sqrt a }} - \frac{{9 - a}}{{a + \sqrt a - 6}}} \right)\) với \(a \geqslant 0;a \ne 4;a \ne 9\)
Tìm giá trị của a để A - 1/A = 0?
| A. a = 5 | B. a = 3 | C. a = 36 | D. a = 25 |
Hướng dẫn giải toán
Ta có:
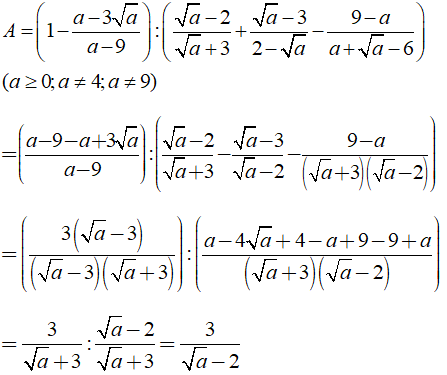
Ta có:
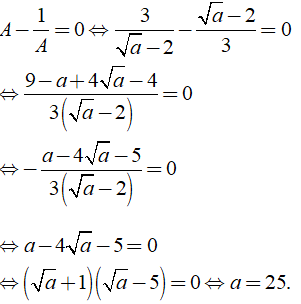
Chọn đáp án D.
IV. Bài tập tự luận có hướng dẫn chi tiết
Câu 1: Cho biểu thức
\(B = \left( {\frac{{x\sqrt x + x + \sqrt x }}{{x\sqrt x - 1}} - \frac{{\sqrt x + 3}}{{1 - \sqrt x }}} \right).\frac{{x - 1}}{{2x + \sqrt x - 1}}\) (với x ≥ 0; x ≠ 1 và x ≠ 1/4).
Tìm tất cả các giá trị của x để B < 0.
Ta có:
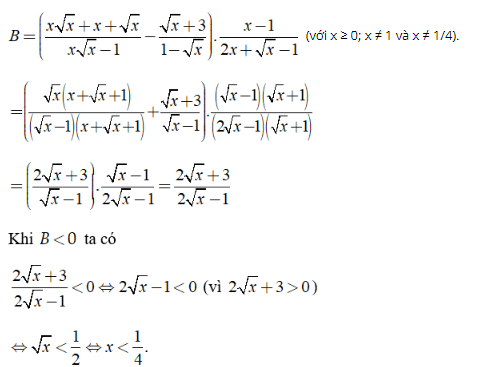
Kết hợp điều kiện ta có x ∈ [0; 1/4].
Câu 2: Giải các phương trình sau:
a. \(\sqrt {1 - x} + \sqrt {{x^2} - 3x + 2} + \left( {x - 2} \right)\sqrt {\frac{{x - 1}}{{x - 2}}} = 2\)
b.\(\left( {x + 1} \right)\left( {x + 4} \right) - 3\sqrt {{x^2} + 5x + 2} = 6\)
c. \(\frac{{6x - 3}}{{\sqrt x - \sqrt {1 - x} }} = 3 + 2\sqrt {x - {x^2}}\)
a) Điều kiện xác định:
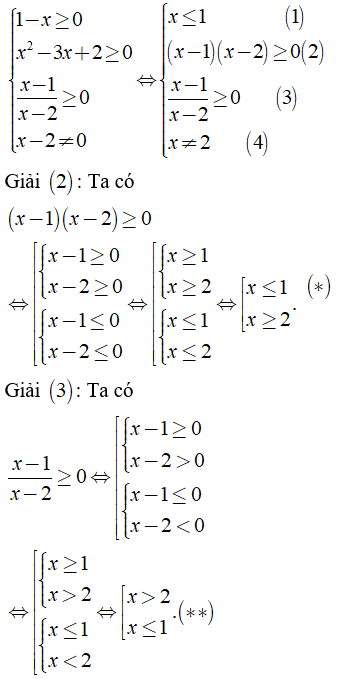
Kết hợp (1), (4), (*) và (**) ta có điều kiện xác định: x ≤ 1
Ta có
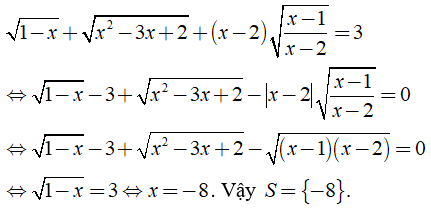
b) Điều kiện xác định: .
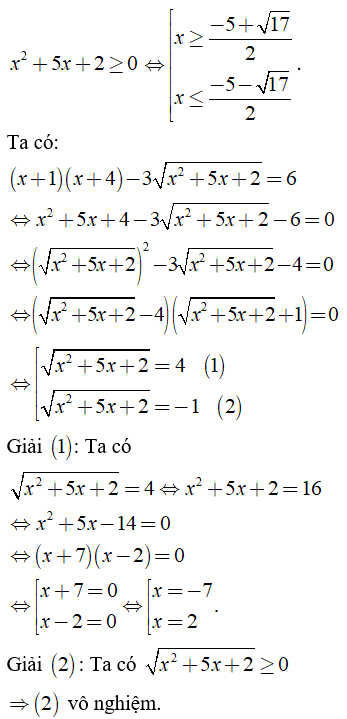
So sánh điều kiện ta có: x = -7; x = 2 (t/m). Vậy S = {-7; 2}.
c) Điều kiện xác định x ∈ [0; 1]\{1/2}.
Ta có:
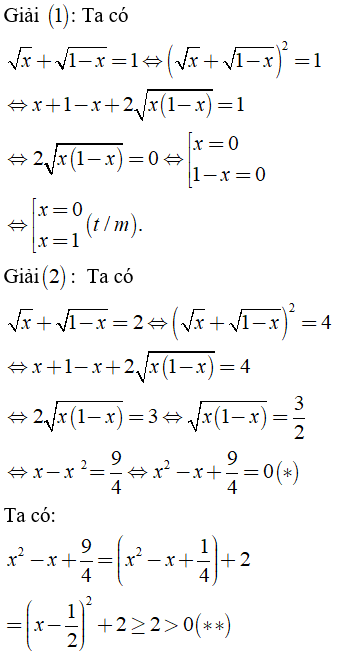
Từ (*) và (**) suy ra phương trình (2) vô nghiệm.
Vậy S = {0; 1}.
Câu 3: Rút gọn các biểu thức sau:
a. \(A = \frac{{\sqrt x - \sqrt y }}{{xy\sqrt {xy} }}:\left[ {\left( {\frac{1}{x} + \frac{1}{y}} \right).\frac{1}{{x + y + 2\sqrt {xy} }} + \frac{2}{{{{\left( {\sqrt x + \sqrt y } \right)}^3}}}.\left( {\frac{1}{{\sqrt x }} + \frac{1}{{\sqrt y }}} \right)} \right]\)
Với \(x = 2 - \sqrt 3 ;y = 2 + \sqrt 3\)
b. \(B = \frac{{2a\sqrt {1 + {x^2}} }}{{\sqrt {1 + {x^2}} - x}}\)
Với \(x = \frac{1}{2}\left( {\sqrt {\frac{{1 - a}}{a}} - \sqrt {\frac{a}{{1 - x}}} } \right);0 < a < 1\)
a) Ta có:
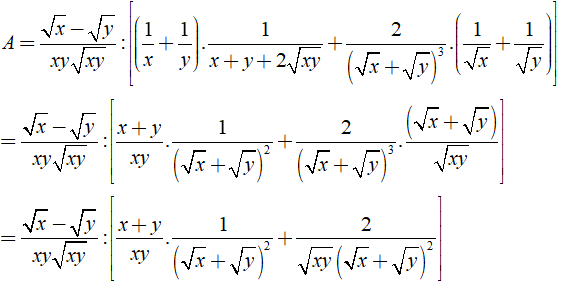
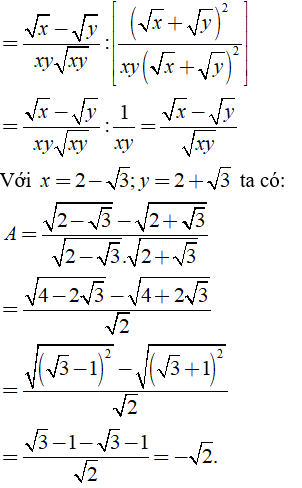
b) Ta có
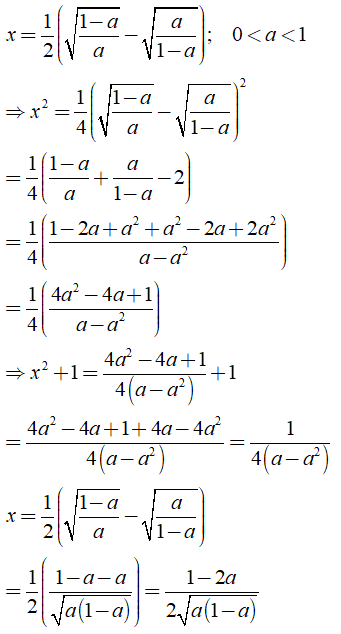
Khi đó: .
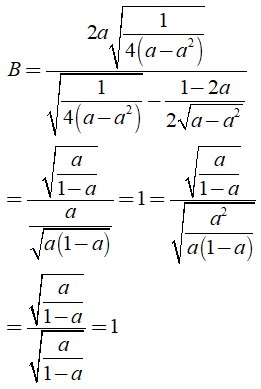
Câu 4: Chứng minh rằng:
\(2\sqrt n - 3 < \frac{1}{{\sqrt 2 }} + \frac{1}{{\sqrt 3 }} + ... + \frac{1}{{\sqrt n }} < 2\sqrt n - 2\) (Với n ∈ N; n ≥ 2)
\(A = \frac{1}{{\sqrt 2 }} + \frac{1}{{\sqrt 3 }} + .... + \frac{1}{{\sqrt n }}\)\(A > 2\sqrt n - 3\). Làm giảm mỗi số hạng của A.\(\frac{1}{{\sqrt k }} = \frac{2}{{\sqrt k + \sqrt k }} > \frac{2}{{\sqrt {k + 1} + \sqrt k }} = 2\left( {\sqrt {k + 1} - \sqrt k } \right)\)\(A > 2\left[ {\left( { - \sqrt 2 + \sqrt 3 } \right) + \left( { - \sqrt 3 + \sqrt 4 } \right) + ... + \left( { - \sqrt n + \sqrt {n + 1} } \right)} \right]\)\(= 2\left( {\sqrt {n + 1} - \sqrt 2 } \right) = 2\sqrt {n + 1} - 2\sqrt 2 > 2\sqrt {n + 1} - 3 > 2\sqrt n - 3\)\(A < 2\sqrt n - 2\)\(\frac{1}{{\sqrt k }} = \frac{2}{{\sqrt k + \sqrt k }} < \frac{2}{{\sqrt {k - 1} + \sqrt k }} = 2\left( {\sqrt k - \sqrt {k - 1} } \right)\)Do đó \(A < 2\left[ {\left( {\sqrt n - \sqrt {n - 1} } \right) + .... + \left( {\sqrt 3 - \sqrt 2 } \right) + \left( {\sqrt 2 - \sqrt 1 } \right)} \right]\)
\(= 2\left( {\sqrt {n + 1} - 2} \right)\)
\(\Rightarrow 2\sqrt n - 3 < \frac{1}{{\sqrt 2 }} + \frac{1}{{\sqrt 3 }} + ... + \frac{1}{{\sqrt n }} < 2\sqrt n - 2;\left( {n \in \mathbb{N},n \geqslant 2} \right)\)
V. Bài tập tự rèn luyện rút gọn biểu thức chứa căn
Câu 1: Cho biểu thức:
P = \(\sqrt{\ x}\ \ \ - \ \ \sqrt{\ x\
\ - \ \ 1}\ \ \ + \ \ \ \frac{1}{\sqrt{\ x\ \ - \ \ 1}\ \ \ - \ \
\sqrt{\ x}\ \ }\ \ \ + \ \ \ \frac{\sqrt{\ x^{3}}\ \ \ - \ \ \
x}{\sqrt{\ x}\ \ \ - \ \ \ 1}\)
a. Tìm điều kiện xác định và rút gọn biểu thức P.
b. Tìm giá trị của x khi P = 1.
Câu 2: Cho biểu thức: \(A = 1 - (\frac{2}{1
+ 2\sqrt{x}} - \frac{5\sqrt{x}}{4x - 1} - \frac{1}{1 -
2\sqrt{x}}):\frac{\sqrt{x} - 1}{4x + 4\sqrt{x} + 1}\)
a) Rút gọn biểu thức A;
b) Tìm giá trị nguyên của x để biểu thức A đạt giá trị nguyên;
c) Tính giá trị của biểu thức A với \(x = -
7\sqrt[3]{49(5 + 4\sqrt{2})(3 + 2\sqrt{1 + 2\sqrt{2}})(3 - 2\sqrt{1 +
2\sqrt{2}})}\).
Bài 3: Cho biểu thức: \(P = \frac{x^{2} -
\sqrt{x}}{x + \sqrt{x} + 1} - \frac{2x + \sqrt{x}}{\sqrt{x}} + \frac{2(x
- 1)}{\sqrt{x} - 1}.\)
a. Rút gọn biểu thức P.
b. Tìm giá trị nhỏ nhất của biểu thức P.
c. Xét biểu thức: \(Q =
\frac{2\sqrt{x}}{P},\) chứng tỏ 0 < Q < 2.
Bài 4: Cho biểu thức \(A = \frac{2\sqrt{x} - 9}{x -5\sqrt{x} + 6} + \frac{2\sqrt{x} + 1}{\sqrt{x} - 3} + \frac{\sqrt{x} +3}{2 - \sqrt{x}};(x \geq 0,x \neq 4,x \neq 9)\)
a) Rút gọn biểu thức A.
b) Tìm giá trị của x để A = \(-
\frac{1}{2}\).
Câu 5: Cho biểu thức: \(A = 1 - (\frac{2}{1
+ 2\sqrt{x}} - \frac{5\sqrt{x}}{4x - 1} - \frac{1}{1 -
2\sqrt{x}}):\frac{\sqrt{x} - 1}{4x + 4\sqrt{x} + 1}\)
a) Rút gọn biểu thức A;
b) Tìm giá trị nguyên của x để A đạt giá trị nguyên;
c) Tính giá trị của A với \(x = -
7\sqrt[3]{49(5 + 4\sqrt{2})(3 + 2\sqrt{1 + 2\sqrt{2}})(3 - 2\sqrt{1 +
2\sqrt{2}})}\).
Bài 6: Cho biểu thức \(A = 1 + (\frac{2x +\sqrt{x} - 1}{1 - x} - \frac{2x\sqrt{x} - \sqrt{x} + x}{1 -x\sqrt{x}}).\frac{x - \sqrt{x}}{2\sqrt{x} - 1}\).
a) Tìm các giá trị của x để \(A = \frac{6 -
\sqrt{6}}{5}\).
b) Chứng minh rằng \(A >
\frac{2}{3}\) với mọi x thoả mãn \(x
\geq 0,\ \ x \neq 1,\ x \neq \frac{1}{4}\).
Bài 7: Cho biểu thức:
\(P = \left( \frac{\sqrt{x}}{\sqrt{x} + 2}+ \frac{8\sqrt{x} + 8}{x + 2\sqrt{x}} - \frac{\sqrt{x} + 2}{\sqrt{x}}\right):\left( \frac{x + \sqrt{x} + 3}{x + 2\sqrt{x}} +\dfrac{1}{\sqrt{x}} \right)\)
a) Tìm x để P có nghĩa và chứng minh rằng P ≤ 1.
b) Tìm x thoả mãn: \(\left( \sqrt{x} + 1
\right).P = 1\)
Bài 8: Cho biểu thức:
\(P = \left( \frac{\sqrt{x} - 3}{2 -
\sqrt{x}} + \frac{\sqrt{x} + 2}{3 + \sqrt{x}} - \frac{9 - x}{x +
\sqrt{x} - 6} \right):\left( 1 - \frac{3\sqrt{x} - 9}{x - 9}
\right)\)
a) Rút gọn biểu thức P.
b) Tìm các giá trị nguyên của x để P nguyên.
---------------------------------------------------------------------
Việc biến đổi đơn giản biểu thức chứa căn thức bậc hai không chỉ giúp rút gọn các biểu thức phức tạp mà còn là bước đệm quan trọng để giải các bài toán nâng cao hơn trong chương trình học. Nắm vững các quy tắc và luyện tập thường xuyên sẽ giúp bạn tăng độ nhạy bén với các dạng bài đưa một thừa số ra ngoài dấu căn, đưa thừa số vào trong dấu căn, khử mẫu của biểu thức dưới dấu căn.... và giải toán nhanh chóng, chính xác hơn. Hy vọng bài viết đã giúp bạn hiểu rõ cách làm và vận dụng được vào thực tế học tập.
