Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
Chuyên đề Toán học lớp 9: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 9 hiệu quả hơn. Mời các bạn tham khảo.
Bài: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
1. Hình nón
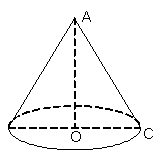
Khi quay tam giác vuông một vòng quanh cạnh OA cố định thì được một hình nón.
+ Điểm A được gọi đỉnh của hình nón.
+ Hình tròn (O) được gọi là đáy của hình nón.
+ Mỗi vị trí của AC được gọi là một đường sinh của hình nón.
+ Đoạn AO được gọi là đường cao của hình nón.
2. Diện tích – thể tích của hình nón
Đặt AC = l; l là đường sinh
Cho hình nón có bán kính đáy R và đường sinh l, chiều cao h.
+ Diện tích xung quanh: Sxq = πRl
+ Diện tích toàn phần: Stp = πRl + πR2
+ Thể tích: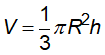
3. Hình nón cụt
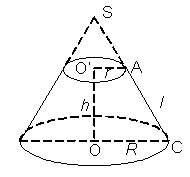
Khi cắt hình nón bởi một mặt phẳng song song với đáy thì phần hình nón nằm giữa mặt phẳng nói trên và mặt phẳng đáy được gọi là một hình nón cụt.
+ Hai hình tròn (O) và (O') được gọi là hai đáy.
+ Đoạn OO' được gọi là trục. Độ dài OO' là chiều cao.
+ Đoạn AC được gọi là đường sinh.
4. Diện tích – thể tích hình nón cụt
Cho hình nón cụt có các bán kính đáy R và r, chiều cao h, đường sinh l.
+ Diện tích xung qaunh: Sxq = π(R + r)l
+ Thể tích: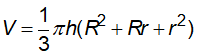
5. Ví dụ cụ thể
Câu 1: Một hình nón có bán kính đáy bằng và diện tích xung quanh là. Tính thể tích của hình nón đó.
Hướng dẫn:

Ta có Sxq = πRl. Theo giả thiết ta có: Sxq = 65π (cm2) ⇒ πRl = 65π (cm2)
Khi đó ta có:
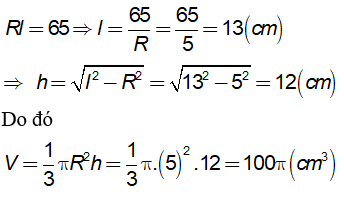
Bài lý thuyết: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt trên đây các bạn học sinh cùng quý thầy cô cần nắm vững kiến thức về khái niệm hình nón, công thức tính diện tích, thể tích của hình nón...







