Đề cương ôn tập học kì 1 Toán 6 Kết nối tri thức
Đề cương ôn tập Toán 6 Học kì 1 theo bộ sách Kết nối tri thức với cuộc sống được biên soạn tỉ mỉ, bám sát chương trình học của Học kì 1, giúp các em học sinh dễ dàng rà soát và nắm vững các chuyên đề trọng tâm của môn Toán 6. Đặc biệt, tài liệu không chỉ tóm tắt lý thuyết mà còn cung cấp một lượng lớn bài tập thực hành đa dạng, bao gồm cả bài tập trắc nghiệm để làm quen với hình thức thi và bài tập tự luận để rèn luyện kỹ năng giải toán chi tiết. Nhờ có đề cương này, học sinh có thể lên kế hoạch ôn tập khoa học, tập trung vào những phần kiến thức còn yếu, từ đó củng cố vững chắc nền tảng và tự tin đạt kết quả cao nhất trong bài thi cuối học kì 1 sắp tới. Mời các bạn tham khảo chi tiết nội dung để bắt đầu quá trình ôn luyện hiệu quả.
Đề cương ôn tập học kì 1 Toán 6
Trọn bộ đề cương ôn tập kì 1 Toán 6 sách mới:
- Đề cương ôn tập học kì 1 môn Toán lớp 6 sách mới
- Đề cương ôn tập Toán 6 học kì 1 sách Chân trời sáng tạo
- Đề cương ôn tập học kì 1 Toán 6 Cánh Diều
Đề tham khảo đầy đủ tài liệu ôn tập, các bạn kéo xuống dưới tải về.
Đề cương ôn tập Toán 6 học kì 1
A/ LÝ THUYẾT
Chương I. Tập hợp các số tự nhiên
- Tập hợp, mô tả một tập hợp
- Ghi số tự nhiên và thứ tự trong tập N.
- Cộng, trừ nhân, chia, lũy thừa trong tập N.
- Thực hiện phép tính, tính giá trị biểu thức số.
Chương II. Tính chia hết trong tập hợp các số tự nhiên
- Quan hệ chia hết và tính chất.
- Dấu hiệu chia hết cho 2, 3, 5, 9; số nguyên tố.
- Ước chung, ước chung lớn nhất; Bội chung, bội chung nhỏ nhất.
Chương III. Số nguyên
- Tập hợp các số nguyên; Cộng, trừ, nhân số nguyên.
- Phép chia hết. Ước và bội của một số nguyên.
- Qui tắc dấu ngoặc.
Chương IV. Một số hình phẳng trong thực tiễn
- Các hình phẳng: hình tam giác đều, hình vuông, hình lục giác đều, hình chữ nhật, hình thoi, hình bình hành, hình thang cân.
- Chu vi và diện tích của hình vuông, hình chữ nhật, hình thang, hình bình hành, hình thoi.
B/ Bài tập tự luận
Chương I. Tập hợp các số tự nhiên
Bài 1:
a) Viết tập hợp A các số tự nhiên lớn hơn 3 và không vượt quá 9 bằng hai cách.
b) Tập hợp B các số tự nhiên khác 0 và không vượt quá 11 bằng hai cách.
c) Viết tập hợp C các số tự nhiên lớn hơn hoặc bằng 15 và không vượt quá 50 bằng hai cách.
Bài 2: Viết Tập hợp các chữ số của các số:
a) 2021
b) 296351
c) 90000
Bài 3: Gọi S là tập hợp các số tự nhiên có hai chữ số. Trong các số 7; 15; 106; ; 99, số nào thuộc và số nào không thuộc tập S? Dùng kí hiệu để trả lời.
Bài 4: Cho hai tập hợp A = {a; b; c} và B = {x; y}. Trong các phần tử a, d, t, y, phần tử nào thuộc tập A, phần tử nào thuộc tập B? Phần tử nào không thuộc tập A, phần tử nào không thuộc tập B. Dùng kí hiệu để trả lời.
Bài 5: Một năm có bốn quý. Đặt tên và viết tập hợp các tháng (dương lịch) của quý Ba trong năm. Tập hợp này có bao nhiêu phần tử?
Bài 6: Cho tập hợp L = {n| n = 2k + 1 với k ∈ N}.
a) Nêu bốn số tự nhiên thuộc tập L và hai số tự nhiên không thuộc tập L;
b) Hãy mô tả tập L bằng cách nêu dấu hiệu đặc trưng theo một cách khác.
Bài 7: Một số tự nhiên có hai chữ số, trong đó chữ số hàng chục lớn hơn chữ số hàng đơn vị là 9. Đó là số nào?
Bài 8: a) Hãy viết số tự nhiên lớn nhất có 5 chữ số.
b) Số tự nhiên nào lớn nhất có 5 chữ số khác nhau?
c) Hãy vẽ tia số và biểu diễn các số 5 và 11 trên tia số đó.
d) Cho bốn tập hợp: A = {x ∈ N| x chẵn và x < 10}, B = {x ∈ N | x chẵn và x ≤ 10},
C = {x ∈ N* | x chẵn và x < 10} và D = {x ∈ N* | x chẵn và x ≤ 10}. Hãy mô tả các tập hợp đó bằng cách liệt kê các phần tử của chúng.
Bài 9: Viết tập hợp các số tự nhiên có ba chữ số mà tổng các chữ số của nó bằng 4.
Bài 10: Tính tổng:
a) 21 + 369 + 79; b) 154 + 87 + 246
c) 215 + 217 + 219 + 221 + 223; d) S = 2. 10 + 2. 12 + 2. 14 + … + 2. 20
Bài 11: Tìm số tự nhiên x biết:
a) x + 257 = 981; b) x – 546 = 35; c) 721 – x = 615
Bài 12: Tính hợp lí:
a) 5. 11. 18 + 9. 31. 10 + 4. 29. 45;
b) 37. 39 + 78. 14 + 13. 85 + 52. 55.
Bài 13:
13.1: Một hình chữ nhật có chiều dài bằng 16cm; diện tích bằng a cm2. Tính chiều rộng của hình chữ nhật (là một số tự nhiên) nếu biết a là một số tự nhiên từ 220 đến 228.
13.2: a) Viết các bình phương của hai mươi số tự nhiên đầu tiên thành một dãy theo thứ tự từ nhỏ đến lớn;
b) Viết các số sau thành bình phương của một số tự nhiên: 64; 100; 121; 169; 196; 289.
c) Viết gọn các tích sau bằng cách dùng lũy thừa: 2. 2. 2. 2. 2.2; 2. 3. 6. 6. 6 và 4. 4. 5. 5. 5.5
Bài 14: Tìm n, biết:
a) 5 4 = n
b) n 3 = 125
c) 11 n = 1331
Bài 15: Gọi P là tập hợp các số tự nhiên chẵn, lớn hơn 2 nhưng không lớn hơn 10.
a) Mô tả tập hợp P bằng hai cách;
b) Biểu diễn các phần tử của tập P trên cùng một tia số.
Bài 16: Lớp 6A có 42 học sinh. Trong đợt thi đua lập thành tích chào mừng Ngày Nhà giáo Việt Nam (20/11), học sinh nào trong lớp cũng được ít nhất một điểm 10. Hãy cho biết trong đợt thi đua đó, lớp 6A được tất cả bao nhiêu điểm 10, biết rằng trong lớp có 39 bạn được từ hai điểm 10 trở lên, 14 bạn được ba điểm 10 trở lên, 5 bạn được bốn điểm 10 và không ai được hơn bốn điểm 10.
Bài 18:
a) Tính S = 1 + 2 – 3 – 4 + 5 + 6 – 7 – 8 + 9 + 10 - … + 2 018 – 2 019 – 2 020 + 2 021
b) Trong một phép chia, số bị chia là 89, số dư là 12. Tìm số chia và thương.
Chương II. Tính chia hết trong tập hợp các số tự nhiên
Bài 19:
19.1. Không làm phép tính, hãy cho biết tổng nào sau đây chia hết cho 5.
a) 80 + 1 945 + 15; b) 1 930 + 100 + 2 021.
19.2. Áp dụng tính chất chia hết của một tổng, hãy tìm x thuộc tập {15; 17; 50; 23} sao cho x + 20 chia hết cho 5.
19.3. Áp dụng tính chất chia hết của một tổng, hãy tìm x thuộc tập {12; 19; 45; 70} sao cho x - 6 chia hết cho 3.
19.4. a) Tại sao tổng 22 + 23 + 24 + 25 chia hết cho 3?
b) Tại sao tổng 420+ 421 + 422 +423 chia hết cho 5?
19.5: Khi chia số tự nhiên a cho 12, ta được số dư là 6. Hỏi a có chia hết cho 2 không? Có chia hết cho 4 không?
Bài : Các tổng sau là số nguyên tố hay hợp số?
a) 2. 7. 12 + 49. 53; b) 3. 4. 5 + 2 020. 2 021. 2 022.
Bài 20: Thực hiện phép tính rồi phân tích kết quả ra thừa số nguyên tố:
a) 122 : 6 + 2.7; b) 5.42– 36 : 32
Bài 21: Số học sinh khối lớp 6 của một trường trong khoảng từ 200 đến 300 học sinh, khi xếp thành các hàng 10; 12 và 15 người đều thừa 5 em. Tính số học sinh khối lớp 6?
Bài 22: Cho A = 27 220 + 31 005 + 510. Không thực hiện phép tính, hãy xét xem A có:
a) chia hết cho 2 không? b) chia hết cho 5 không?
c) chia hết cho 3 không? d) chia hết cho 9 không?
Bài 23: Hai số có BCNN là 23.34.53 và ƯCLN là 32.5. Biết một trong hai số là 23.32.5, tìm số còn lại.
Bài 24:
a) Tìm các số tự nhiên n sao cho 6 ⁝ (n+1).
b)Biết hai số 23.3avà 2b.35 có ước chung lớn nhất là 22.35 và bội chung nhỏ nhất là 23.36. Hãy tìm giá trị của các số tự nhiên a và b.
II. BÀI TẬP TRẮC NGHIỆM
Bài 1: Khoanh tròn vào chữ cái trước câu trả lời đúng:
Câu 1: Ba số nào sau đây là ba số tự nhiên liên tiếp tăng dần:
A. b – 1; b; b + 1 ( b ∈ N).
B. b; b + 1; b + 2 ( b∈ N).
C. 2b; 3b; 4b ( b ∈ N).
D. b + 1; b; b - 1 (b ∈N)..
Câu 2: Giá trị của tổng ![]() \(M=1+3+5+7+\ldots+97+99\) là:
\(M=1+3+5+7+\ldots+97+99\) là:
A. 5050.
B. 2500.
C. 5000.
D. 2450.
Câu 3: Kết quả của phép tính ![]() \(5^{7} \cdot 18-5^{7} \cdot 13\)bằng:
\(5^{7} \cdot 18-5^{7} \cdot 13\)bằng:
A. 5.
B. 58
C. 57
D. 56
Câu 4: Biết ![]() \(\left[(x-3)^{2}+7\right] \cdot 2=14\). Vậy giá trị của là:
\(\left[(x-3)^{2}+7\right] \cdot 2=14\). Vậy giá trị của là:
A. x = 0.
B. x = 3.
C. x = 7.
D. x = 3 và x = 7.
Câu 5: Cho số ![]() \(M=\overline{16 * 0}\)chữ số thích hợp để M chia hết là:
\(M=\overline{16 * 0}\)chữ số thích hợp để M chia hết là:
A. 2.
B. 8.
C. 4.
D. 5.
Bài 2: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
|
Câu |
Khẳng định |
Đúng |
Sai |
| 1 |
Nếu mỗi số hạng của tổng chia hết cho 5 thì tổng chia hết cho 5 |
|
|
| 2 |
Nếu mỗi số hạng của tổng không chia hết cho 7 thì tổng không chia hết cho 7 |
|
|
| 3 |
Nếu tổng của hai số chia hết cho 7 và một trong hai số đó chia hết cho 7 thì số còn lại cũng chia hết cho 7 |
|
|
| 4 |
Nếu hiệu của hai số chia hết cho 5 và một trong hai số đó chia hết cho 5 thì số còn lại cũng chia hết cho 5 |
|
|
| 5 |
Số chia hết cho 7 là hợp số |
|
|
| 6 |
Số chẵn không là số nguyên tố |
|
|
| 7 |
Số nguyên tố lớn hơn 5 thì không chia hết cho 5 |
|
|
| 8 |
Ước chung lớn nhất của hai số lớn hơn 1 là số nguyên tố |
|
|
| 9 |
Số chia hết cho 9 thì chia hết cho 3 |
|
|
| 10 |
Số chia hết cho 3 thì chia hết cho 9 |
|
|
| 11 |
Nếu một thừa số của tích chia hết cho 7 thì tích chia hết cho 7 |
|
|
| 12 |
Tổng 673 + 957 chia hết cho 2 và 5 |
|
|
| 13 |
Số 97 là số nguyên tố |
|
|
| 14 |
Số (2.5.6 - 2.29) là hợp số |
|
|
| 15 |
ƯCLN (15,45,60) = 15 |
|
|
| 16 |
BC (4, 45, 60) = 15 |
|
|
| 17 |
Hai số 237 và 873 là hai số nguyên tố cùng nhau |
|
|
| 18 |
Mọi số nguyên tố lớn hơn 5 chỉ có thể tận cùng là 1; 3; 7; 9 |
|
|
| 19 |
Tổng của hai số nguyên đối nhau là 0 |
|
|
| 20 |
Tích của hai số nguyên âm là một số nguyên âm |
|
|
| 21 |
Nếu tích của hai số nguyên là một số nguyên dương thì hai số |
|
|
| 22 |
đó trái dấu nhau |
|
|
| 23 |
5 là uớc của 15 nhưng -5 không phải là ước của 15. |
|
|
Bài 3: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
|
Câu |
Khẳng định |
Đúng |
Sai |
| 1 |
Tam giác đều là tam giác có ba cạnh bằng nhau. |
|
|
| 2 |
Hình thoi có bốn góc bằng nhau. |
|
|
| 3 |
Giao điểm hai đường chéo của hình bình hành cắt nhau tại trung điểm của mỗi đường. |
|
|
| 4 |
Hình vuông có hai đường chéo vuông góc với nhau. |
|
|
BÀI TẬP TỰ ÔN
SỐ HỌC
Dạng 1. Thực hiện phép tính:
Bài 5: Thực hiện các phép tính sau (tính hợp lí nếu có thể)
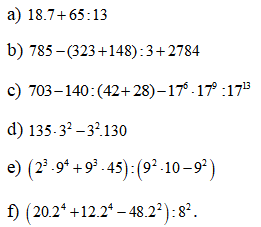
Bài 6: Thực hiện các phép tính sau:
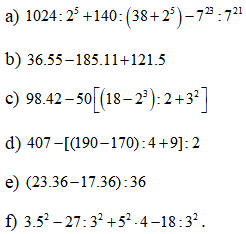
Tài liệu vẫn còn dài, mời các bạn tải về để xem trọn bộ
Đề thi học kì 1 lớp 6 sách mới
- Đề thi học kì 1 lớp 6 môn Toán sách mới
- Đề thi học kì 1 môn Toán lớp 6 Chân trời sáng tạo
- Đề thi học kì 1 Toán 6 Kết nối tri thức với cuộc sống
- Đề thi học kì 1 Toán 6 sách Cánh Diều









