Đề thi học kì 1 Toán 6 Cánh diều Số 2

Đề thi học kì 1 môn Toán lớp 6 (Số 2) được biên soạn chất lượng, bám sát chương trình học theo bộ sách Cánh Diều, là tài liệu ôn tập không thể thiếu cho kì thi cuối học kì I.

Đề thi bao gồm đầy đủ cả phần trắc nghiệm và tự luận, giúp học sinh rèn luyện kỹ năng làm bài và làm quen với cấu trúc đề thi chính thức. Đặc biệt, đề thi được cung cấp dưới cả hai định dạng file Word và PDF, rất thuận tiện cho quý thầy cô giáo tham khảo ra đề, chỉnh sửa và ôn tập cho học sinh. Đồng thời, đây cũng là nguồn tài liệu hay và hữu ích để các em học sinh tự luyện tập và củng cố kiến thức để đạt kết quả cao nhất trong kì thi sắp tới.

Đề thi học kì 1 lớp 6 môn Toán 

Dưới đây là một phần của đề thi học kì 1 môn Toán lớp 6, mời xem thử. Tải về xem trọn bộ.

I. Phần trắc nghiệm (2 điểm)

Câu 1: Cho tập hợp M = {a, b, c}. Cách viết nào sau đây là đúng?

A) b ∈ M

B) d ∈ M

C) {a} ∈ M

D) c ∉ M

..................

Câu 4: Đối với các phép toán có dấu ngoặc, thứ tự thực hiện phép tính là

A) {} → [] → ()

B) () → [] → {}

C) {} → () → []

D) [] → () → {}

II. Tự luận

Bài 1 (3 điểm): Thực hiện phép tính

a) 27.16 + 81.21 + 9.21.3

b) 36.13 + 65.37 + 9.4.87 + 65.9.7

c) 2².85 + 15.2² - 2020⁰

d) 123.456 + 456.321 - 256.444

..................

Bài 4 (0,5 điểm): Cho hình chữ nhật ABCD. Gọi E, H, G lần lượt là trung điểm của AB, CD, EB. Tính tỉ số diện tích của diện tích hình thang GBCH và diện tích hình thang AGHD.

***************
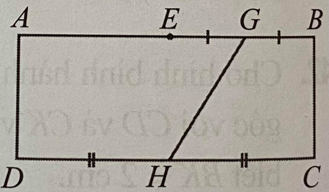