Đề cương ôn tập học kì 1 Toán 8 Kết nối tri thức năm 2024 - 2025

VnDoc giới thiệu Đề cương ôn tập học kì 1 Toán 8 Kết nối tri thức cho các em tham khảo và luyện tập. Đây không chỉ là tài liệu hay cho các em ôn luyện trước kỳ thi mà còn là tài liệu cho thầy cô tham khảo ra đề. Sau đây là nội dung đề cương ôn thi Toán 8, mời thầy cô và các em tham khảo.

1. Tóm tắt kiến thức

CÁC HẰNG ĐẲNG THỨC ĐÁNG NHỚ VÀ ỨNG DỤNG.

Rút gọn biểu thức. Hằng đẳng thức lập phương của một tổng, một hiệu, tổng và hiệu hai lập phương, tính giá trị biểu thức, tìm x.

* Nhận biết:

– Nhận biết được các khái niệm: đồng nhất thức, hằng đẳng thức.

* Thông hiểu:

– Mô tả được các hằng đẳng thức: bình phương của tổng và hiệu; hiệu hai bình phương; lập phương của tổng và hiệu; tổng và hiệu hai lập phương.
Phân tích đa thức thành nhân tử.

* Vận dụng:

– Vận dụng được các hằng đẳng thức để phân tích đa thức thành nhân tử ở dạng: vận dụng trực tiếp hằng đẳng thức.

– Vận dụng hằng đẳng thức thông qua nhóm hạng tử và đặt nhân tử chung.

2. ĐỊNH LÍ THALÈS TRONG TAM GIÁC.

Định lí Thalès trong tam giác.

*  Nhận biết:

– Nhận biết được định nghĩa đường trung bình của tam giác.

* Thông hiểu:

– Giải thích được tính chất đường trung bình của tam giác (đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh đó).

– Giải thích được định lí Thalès trong tam giác (định lí thuận và đảo).

– Giải thích được tính chất đường phân giác trong của tam giác.

* Vận dụng:

– Tính được độ dài đoạn thẳng bằng cách sử dụng định lí Thalès.

– Giải quyết được một số vấn đề thực tiễn (đơn giản, quen thuộc) gắn với việc vận dụng định lí Thalès (ví dụ: tính khoảng cách giữa hai vị trí).

* Vận dụng cao:

– Giải quyết được một số vấn đề thực tiễn (phức hợp, không quen thuộc) gắn với việc vận dụng định lí Thalès.

3. DỮ LIỆU VÀ BIỂU ĐỒ.

Thu thập, phân loại, tổ chức dữ liệu theo các tiêu chí cho trước.

* Vận dụng:

– Thực hiện và lí giải được việc thu thập, phân loại dữ liệu theo các tiêu chí cho trước từ nhiều nguồn khác nhau: văn bản; bảng biểu; kiến thức trong các lĩnh vực giáo dục khác (Địa lí, Lịch sử, Giáo dục môi trường, Giáo dục tài chính, …); phỏng vấn, truyền thông, Internet; thực tiễn (môi trường, tài chính, y tế, giá cả thị trường, …).

– Chứng tỏ được tính hợp lí của dữ liệu theo các tiêu chí toán học đơn giản (ví dụ: tính hợp lí trong các số liệu điều tra; tính hợp lí của các quảng cáo, …).

* Nhận biết:

– Nhận biết được mối liên hệ toán học đơn giản giữa các số liệu đã được biểu diễn. Từ đó, nhận biết được số liệu không chính xác trong những ví dụ đơn giản.

* Thông hiểu:

– Mô tả được cách chuyển dữ liệu từ dạng biểu diễn này sang dạng biểu diễn khác.

Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ.

* Vận dụng:

– Lựa chọn và biểu diễn được dữ liệu vào bảng, biểu đồ thích hợp ở dạng: bảng thống kê; biểu đồ tranh; biểu đồ dạng cột/cột kép (column chart), biểu liệu và biểu đồ thống kê đã có đồ hình quạt tròn (cho sẵn) (pie chart); biểu đồ đoạn thẳng (line graph).

– So sánh được các dạng biểu diễn khác nhau cho một tập dữ liệu.

Bài tập ôn tập học kì 1 Toán 8

I. Phần trắc nghiệm

Câu 1: Tính giá trị biểu thức \(B = 5{x^2} - 3x - 18\) tại \(\left| x \right| = 3\).

A. \(B = 18\).

B. \(B = 18\) hoặc \(B = 36\).

C. \(B = 36\).

D. \(B = - 18\) hoặc \(B = 36\).

Câu 2: Cho \(A = 4{x^4} + 2{y^2}x - 3{z^3} + 5\) và \(B = - 4{z^3} + 8 + 3{y^2}x - 5{x^4}\). Kết quả của \(A - B\) là:

A. \(9{x^4} + {y^2}x + {z^3} - 3\).

B. \(- {x^4} + 5{y^2}x + {z^3} + 13\).

C. \(9{x^4} - {y^2}x + {z^3} - 3\).

D. \(9{x^4} - {y^2}x + {z^3} + 3\).

Câu 3: Thương \(\left( { - 12{x^4}y + 4{x^3} - 8{x^2}{y^2}} \right):\left( { - 4{x^2}} \right)\) bằng

A. \(- 3{x^2}y + x - 2{y^2}\).

B. \(3{x^4}y + {x^3} - 2{x^2}{y^2}\).

C. \(- 12{x^2}y + 4x - 2{y^2}\).

D. \(3{x^2}y - x + 2{y^2}\).

Câu 4: Kết quả của tích \(\left( {2x + y} \right)\left( {2x - y} \right)\) là:

A. \(4x - y\).

B. \(4x + y\).

C. \(4{x^2} - {y^2}\).

D. \(4{x^2} + {y^2}\).

Câu 5: Kết quả \(8{x^3} + 12{x^2}y + 6x{y^2} + {y^3}\) là:

A. \({\left( {2{x^3} + y} \right)^3}\).

B. \({\left( {2x + {y^3}} \right)^3}\).

C. \({\left( {2x + y} \right)^3}\).

D. \({\left( {2x - y} \right)^3}\).

Câu 6: Điền đơn thức vào chỗ trống: \(\left( {3x + y} \right)\left( {....... - 3xy + {y^2}} \right) = 27{x^3} + {y^3}\)

A. \(9x\).

B. \(6{x^2}\).

C. \(9xy\).

D. \(9{x^2}\).

Câu 7: Đa thức \(12x - 9 - 4{x^2}\) được phân tích thành

A. \(\left( {2x - 3} \right)\left( {2x + 3} \right)\).

B. \(- {\left( {2x - 3} \right)^2}\).

C. \({\left( {3 - 2x} \right)^2}\).

D. \(- {\left( {2x + 3} \right)^2}\).

Câu 8: Cho \(ab\left( {x - 5} \right) - {a^2}\left( {5 - x} \right) = a\left( {x - 5} \right)\left( {...} \right)\). Biểu thức thích hợp điền vào dấu … là

A. 2a + b.

B. 1 + b.

C. a2 + ab.

D. a + b.

Câu 9: Hình bình hành là tứ giác có

A. hai cạnh song song.

B. các cạnh đối song song.

C. các góc bằng nhau.

D. các góc đối bù nhau.

Câu 10: Hai đường chéo của hình chữ nhật

A. song song với nhau.

B. bằng nhau.

C. vuông góc với nhau.

D. là các đường phân giác của các góc.

Câu 11: Một tứ giác là hình vuông nếu nó

A. có ba góc vuông.

B. là hình thoi có một góc vuông.

C. là hình bình hành có một góc vuông.

D. là hình thang có hai góc vuông.

Câu 12: Hình thang cân là hình thang

A. có hai cạnh bên bằng nhau.

B. có hai cạnh đáy bằng nhau.

C. có hai góc kề một cạnh bên bù nhau.

D. có hai góc kề một đáy bằng nhau.

Câu 13: Khẳng định nào sau đây là sai?

A. Hình thang cân có một góc vuông là hình chữ nhật.

B. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

C. Hình bình hành có hai đường chéo vuông góc với nhau là hình chữ nhật.

D. Tứ giác có bốn góc bằng nhau là hình chữ nhật.

Câu 14: Cho tam giác ABC có AM là đường trung tuyến, ta có:

A. \({S_{\Delta ABM}} = 2{S_{\Delta ABC}}\).

B. \({S_{\Delta ABM}} = {S_{\Delta ABC}}\).

C. \({S_{\Delta AMC}} = 2{S_{\Delta ABC}}\).

D. \({S_{\Delta ABC}} = 2{S_{\Delta ABM}}\).

Câu 15: Cho tam giác ABC, qua điểm D thuộc cạnh BC, kẻ các đường thẳng song song với AB và AC, cắt AC và AB theo thứ tự tại E và F. Tam giác ABC cần thêm điều kiện gì để AEDF là hình chữ nhật?

A. cân tại A.

B. vuông tại A.

C. \(\widehat B = {60^o}\).

D. \(\widehat B = {30^0}\).

Câu 16: Cho tam giác ABC, D là trung điểm của BC. Qua D kẻ các đường thẳng song song với AB và AC, cắt AC và AB theo thứ tự ở E và F. Tam giác ABC cần thêm điều kiện gì để AEDF là hình vuông?

A. cân tại A.

B. vuông tại A.

C. vuông cân tại A.

D. \(\widehat A = {60^0}\).

Câu 17: Hình bình hành cần thêm điều kiện gì để trở thành hình vuông?

A. Hai đường chéo bằng nhau.

B. Hai đường chéo cắt nhau tại trung điểm mỗi đường.

C. Hai cạnh kề bằng nhau.

D. Có một góc vuông và hai đường chéo vuông góc với nhau.

Câu 18: Cho tam giác ABC có ba đường trung tuyến AI, BD, CE đồng quy tại G. Gọi M và N lần lượt là trung điểm của GC và GB. Khi đó tứ giác MNED là hình gì?

A. Hình chữ nhật.

B. Hình bình hành.

C. Hình thang cân.

D. Hình thang vuông.

Câu 19: Viết tỉ số cặp đoạn thẳng có độ dài như sau: AB = 4dm, CD = 20dm.

A. \(\frac{{AB}}{{CD}} = \frac{1}{4}\).

B. \(\frac{{AB}}{{CD}} = \frac{1}{5}\).

C. \(\frac{{AB}}{{CD}} = \frac{1}{6}\).

D. \(\frac{{AB}}{{CD}} = \frac{1}{7}\).

Câu 20: Cho \(\Delta ABC\) có AB = 9 cm; D \(\in\) AB sao cho AD = 6cm. Kẻ DE // BC (E \(\in\) AC); EF // CD (F \(\in\) AB). Tính độ dài AF.

A. 6cm.

B. 5cm.

C. 4cm.

D. 7cm.

Câu 21: Cho hình thang ABCD (AB // CD); BC = 15cm, E \(\in\) AD; \(\frac{{AE}}{{AD}} = \frac{1}{3}\). Qua E kẻ đường thẳng song song với CD cắt BC tại F. Tính độ dài BF.

A. 15cm.

B. 5cm.

C. 10cm.

D. 7cm.

Câu 22: Cho \(\Delta ABC\), AC = 2AB, AD là tia phân giác của tam giác ABC, khi đó \(\frac{{BD}}{{CD}} = ?\)

A. \(\frac{{BD}}{{CD}} = 1\).

B. \(\frac{{BD}}{{CD}} = \frac{1}{3}\).

C. \(\frac{{BD}}{{CD}} = \frac{1}{4}\).

D. \(\frac{{BD}}{{CD}} = \frac{1}{2}\).

Câu 23: Cho \(\Delta ABC\) có chu vi 80cm. Gọi D, E, F là trung điểm của các cạnh AB, AC, BC. Chu vi của \(\Delta DEF\) là:

A. 40cm.

B. 160cm.

C. 80cm.

D. 20cm.

Câu 24: Cho \(\Delta ABC\) có D, E lần lượt là trung điểm của AB, AC và DE = 4cm. Biết đường cao AH = 6cm. Diện tích tam giác ABC là

A. \(S = 24c{m^2}\).

B. \(S = 48c{m^2}\).

C. \(S = 12c{m^2}\).

D. \(S = 32c{m^2}\).

Câu 25: Cho \(\Delta ABC\), các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K lần lượt là trung điểm của GB và GC. Tính EI, DK biết AG = 4cm.

A. EI = DK = 3cm.

B. EI = 3cm, DK = 2cm.

C. EI = DK = 2cm.

D. EI = 1cm, DK = 2cm.

Câu 26: Trong các dữ liệu sau dữ liệu nào là dữ liệu định tính?

A. Số huy chương vàng mà các động viên đã đạt được.

B. Danh sách các động viên tham dự Olympic 2021: Nguyễn Văn Hoàng,……

C. Số học sinh nữ của các tổ trong lớp 7A.

D. Năm sinh của các thành viên trong gia đình em.

II. Phần tự luận

Bài 1. Thực hiện các phép tính:

a) \(\left( {x + 3} \right)\left( {x - 3} \right)\).

b) \(\frac{1}{2}x{y^2}.\left( {6xy + \frac{3}{2}{x^3}y - 1} \right)\).

c) \(\left( {2x - y} \right)\left( {4{x^2} + 2xy + {y^2}} \right)\).

d) \(\left( {6{x^5}{y^2} - 9{x^4}{y^3} + 15{x^3}{y^4}} \right):3{x^3}{y^2}\).

Bài 2. Rút gọn các biểu thức:

a) \({\left( {x + y} \right)^2} - {\left( {x - y} \right)^2}\)

b) \(\left( {x + 3} \right)\left( {x + 7} \right) - \left( {x + 1} \right)\left( {x - 1} \right)\)

Bài 3. Phân tích các đa thức sau thành nhân tử:

a) \({x^2} - {y^2} - 2x + 2y\)

b) \({x^2} - 25 + {y^2} + 2xy\)

c) \({x^2}\left( {x - 1} \right) + 16\left( {1 - x} \right)\)

d) \({x^2} + 8x + 15\)

e) \({x^2} - x - 12\)

f) \({\left( {{x^2} + x} \right)^2} + 3\left( {{x^2} + x} \right) + 2\)

Bài 4. Tìm x, biết:

a) \(2x\left( {x - 5} \right) - x\left( {3 + 2x} \right) = 26\)

b) \(\left( {4x - 1} \right)\left( {x + 3} \right) - {\left( {2x - 1} \right)^2} = 0\)

c) \(5x\left( {x - 1} \right) = x - 1\)

d) \(2\left( {x + 5} \right) - {x^2} - 5x = 0\)

e) \({\left( {2x - 3} \right)^2} - {\left( {x + 5} \right)^2} = 0\)

f) \(3{x^3} - 48x = 0\)

Bài 5. Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến.

a) \(A = 2xy + \frac{1}{2}x.\left( {2x - 4y + 4} \right) - x\left( {x + 2} \right)\)

b) \(B = {\left( {x + 2} \right)^2} - {\left( {x - 3} \right)^2} - 10x\)

Bài 6. Biểu đồ hình quạt tròn ở hình bên biểu diễn tỉ lệ các yếu tố ảnh hưởng đến sinh trưởng của cây trồng như: Phân bón; Nước tưới; Giống; Kiểm soát dịch hại; Kiểm soát cỏ dại; Yếu tố khác.

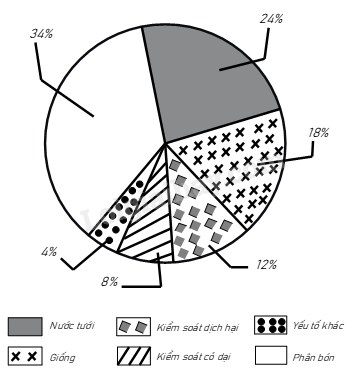
a) Cho biết yếu tố nào ảnh hưởng đến sinh trưởng của cây trồng nhiều nhất?

b) Trong các yếu tố ảnh hưởng đến sinh trưởng của cây thì yếu tố kiểm soát dịch hại gấp mấy lần yếu tố khác?

Bài 7. Cho hình thang ABCD (AB // CD), M là trung điểm của CD. Gọi E là giao điểm của AC và BM, F là giao điểm của BD và AM. Đường thẳng EF cắt BC và AD lần lượt tại G và H.

a) Chứng minh rằng \(\frac{{EA}}{{EC}} = \frac{{2AB}}{{CD}}\).

b) Chứng minh rằng EF // CD.

c) Chứng minh rằng GE = EF = FH.

Bài 8. Cho hình bình hành ABCD, M là trung điểm của AB. Gọi G là giao điểm của AC và DM. Lấy điểm E thuộc đoạn thẳng AM. Các đường thẳng GE và CD cắt nhau tại F.

a) Chứng minh rằng G là trọng tâm của tam giác ABD.

b) Chứng minh rằng GC = 2GA.

c) Kẻ đường thẳng qua G cắt các cạnh AD và BC lần lượt tại I và K. Chứng minh rằng EI // KF.

d) Gọi N là trung điểm của AD. Chứng minh rằng BF = 2EN.

Bài 9. Cho hình vuông ABCD có tâm O, gọi E là trung điểm của AB, DE cắt AC tại F, BF cắt CD tại I.

a) Chứng minh D là trung điểm của IC.

b) Chứng minh ABDI là hình bình hành.

c) Gọi H là trung điểm của AI, CH cắt BD tại L. Chứng minh L là trung điểm của OD.

Bài 10*. Tính GTNN của biểu thức \(B = {x^2} + 2{y^2} + 3{z^2} - 2xy + 2xz - 2x - 2y - 8z + 2000\).

Bài 11*. Cho a + b = 1. Tính giá trị của biểu thức sau:

\(M = {a^3} + {b^3} + 3ab\left( {{a^2} + {b^2}} \right) + 6{a^2}{b^2}\left( {a + b} \right)\).