Đường thẳng vuông góc với mặt phẳng Kết nối tri thức
Bộ tài liệu Lí thuyết Toán 11 Kết nối tri thức: Đường thẳng vuông góc với mặt phẳng bao gồm định nghĩa, tính chất của đường thẳng vuông góc với mặt phẳng và liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng. Ngoài ra có các bài tập ứng dụng có hướng dẫn chi tiết, được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 11 KNTT giúp các em dễ dàng ôn tập củng cố.
1. Đường thẳng vuông góc với mặt phẳng
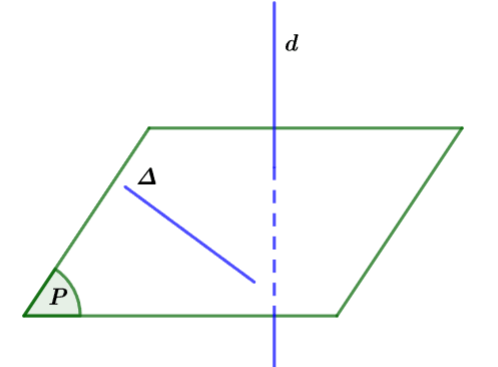
Đường thẳng 
\(∆\) được gọi là vuông góc với mặt phẳng \((P)\) nếu \(∆\) vuông góc với đường thẳng nằm trong \((P)\).
Hình vẽ minh họa
Chú ý: Khi \(∆\) vuông góc với \((P)\) ta còn nói \((P)\) vuông góc với \(∆\) hoặc \(∆\) và \((P)\) vuông góc với nhau, kí hiệu là \(\Delta \bot \left( P \right)\).
Định lí: Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.
| \(\left\{ {\begin{array}{*{20}{l}}
{a,{\text{ }}b \subset \left( \alpha \right)} \\
{a{\text{ }} \cap {\text{ }}b = O} \\
{d \bot a} \\
{d \bot b}
\end{array}} \right. \Rightarrow d \bot \left( \alpha \right)\) |
 |
Ví dụ: Cho hình chóp \(S.ABCD\) có đáy là một hình vuông và SA vuông góc với mặt phẳng đáy. Chứng minh:
a) \(BC \bot \left( {SAB} \right)\)
b) \(BD \bot \left( {SAC} \right)\)
Hướng dẫn giải
Hình vẽ minh họa
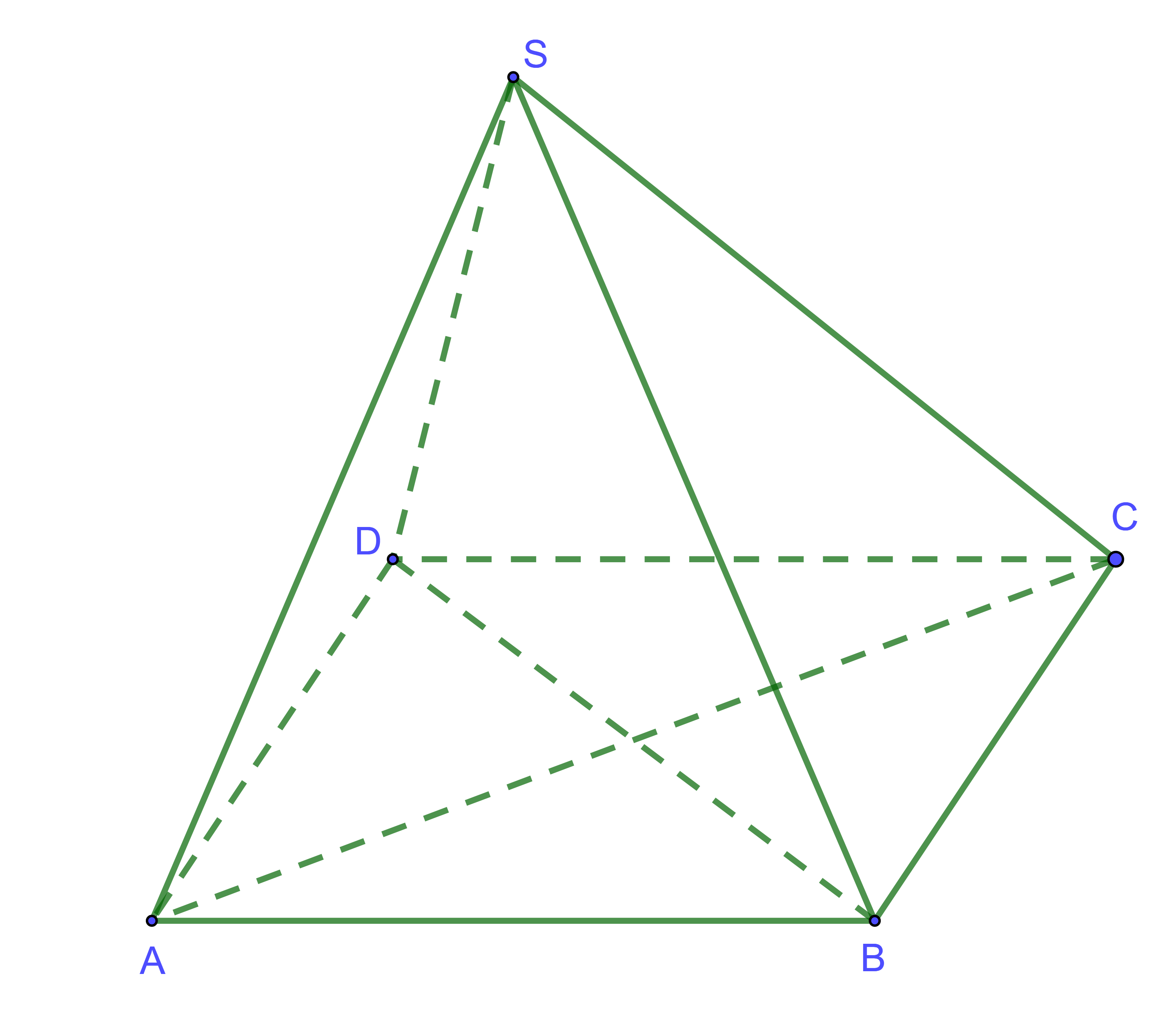
Theo bài ra: SA vuông góc với mặt phẳng đáy hay \(SA \bot \left( {ABCD} \right)\)
a) Ta có: \(\left\{ \begin{gathered}
SA \bot \left( {ABCD} \right) \hfill \\
BC \subset \left( {ABCD} \right) \hfill \\
\end{gathered} \right. \Rightarrow SA \bot BC\)
Mà \(BC \bot AB\)
Khi đó ta có: \(\left\{ \begin{gathered}
BC \bot AB \hfill \\
SA \bot BC \hfill \\
SA \cap AB = \left\{ A \right\} \hfill \\
\end{gathered} \right. \Rightarrow BC \bot \left( {SAB} \right)\)
b) Ta có: \(\left\{ \begin{gathered}
SA \bot \left( {ABCD} \right) \hfill \\
BD \subset \left( {ABCD} \right) \hfill \\
\end{gathered} \right. \Rightarrow SA \bot BD\)
Mà \(BD \bot AC\)
Khi đó ta có: \(\left\{ \begin{gathered}
BD \bot AC \hfill \\
SA \bot BD \hfill \\
SA \cap AC = \left\{ A \right\} \hfill \\
\end{gathered} \right. \Rightarrow BD \bot \left( {SAC} \right)\)
Hệ quả: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó cũng vuông góc với cạnh thứ ba của tam giác đó.
2. Tính chất
Tính chất 1: Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
Hình vẽ minh họa
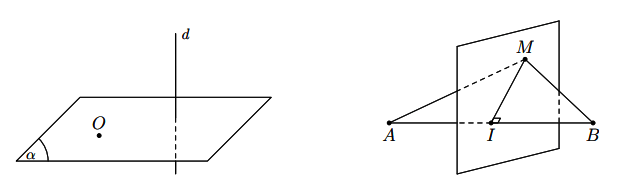
Chú ý: Mặt phẳng đi qua trung điểm của AB và vuông góc với đường thẳng AB được gọi là mặt phẳng trung trực của đoạn thẳng AB. Mặt phẳng trung trực của đoạn thẳng AB là tập hợp các điểm cách đều hai điểm A và B.
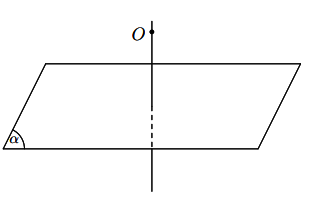
Tính chất 2: Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Hình vẽ minh họa
3. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng
Tính chất 1:
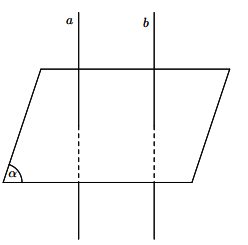
- Nếu đường thẳng a vuông góc với mặt phẳng \((P)\) thì các đường thẳng song song với a cũng vuông góc với \((P)\).
- Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Hình vẽ minh họa
Tính chất 2:
- Nếu đường thẳng \(∆\) vuông góc với mặt phẳng \((P)\) thì \(∆\) cũng vuông góc với các mặt phẳng song song với \((P)\).
- Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
Hình vẽ minh họa
Ví dụ: Cho hình hộp \(ABCD.A’B’C’D’\) có \(ABCD\) là hình thoi, \(AA' \bot \left( {ABCD} \right)\). Chứng minh rằng: \(BB' \bot \left( {A'B'C'D'} \right)\)
Hướng dẫn giải
Hình vẽ minh họa
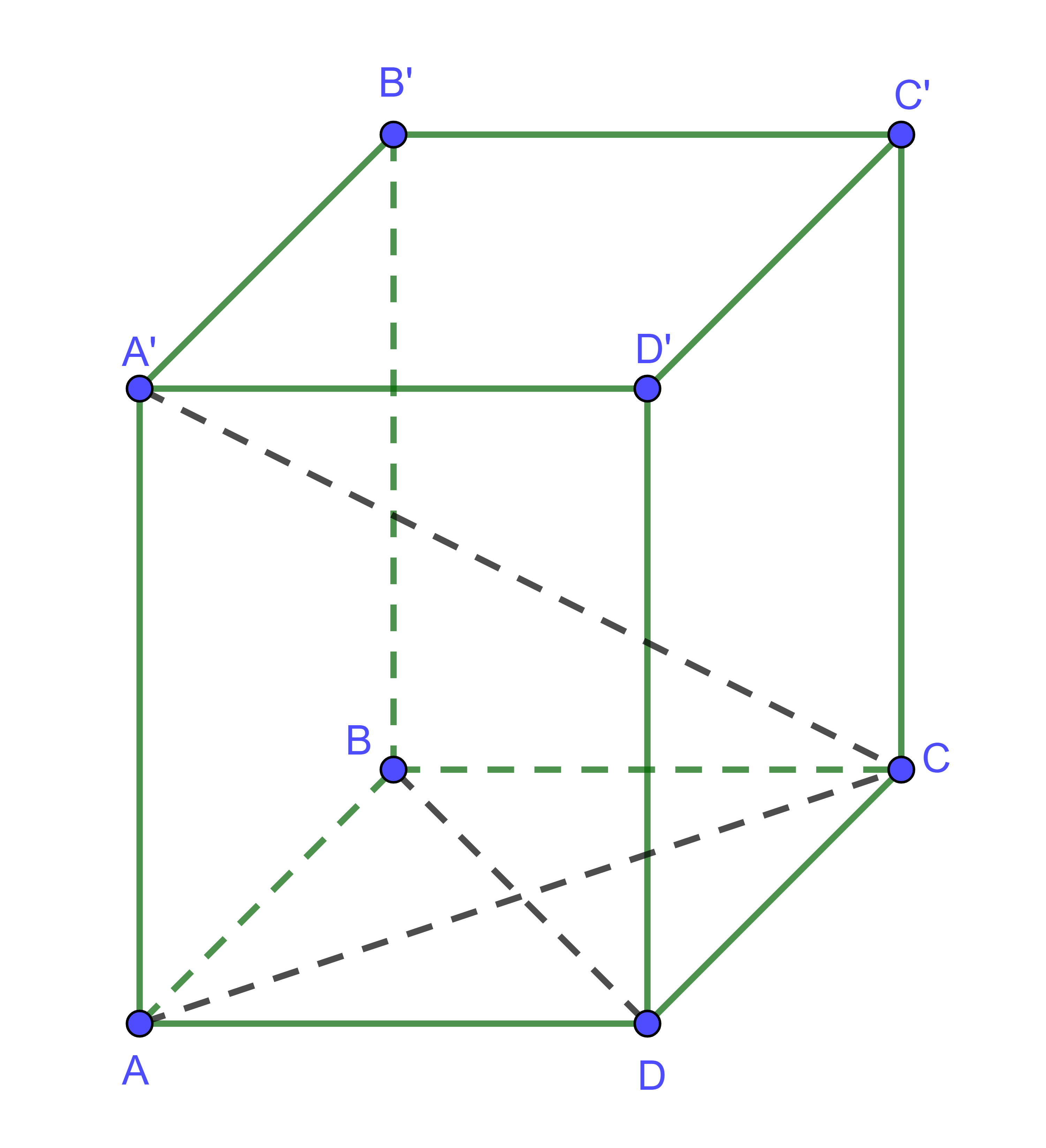
Vì ABCD.A’B’C’D’ là hình hộp nên \(AA’//BB’\)
Mà \(AA' \bot \left( {ABCD} \right) \Rightarrow BB' \bot \left( {ABCD} \right)\)
Ngoài ra ta cũng có \(\left( {ABCD} \right)//\left( {A'B'C'D'} \right)\) nên \(BB' \bot \left( {A'B'C'D'} \right)\).
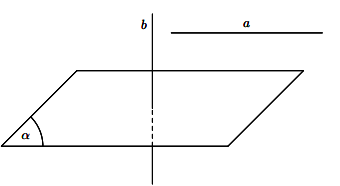
Tính chất 3:
- Nếu đường thẳng \(∆\) vuông góc với mặt phẳng \((P)\) thì \(∆\) vuông góc với mọi đường thẳng song song với \((P)\).
- Nếu đường thẳng a và mặt phẳng \((P)\) cùng vuông góc với một đường thẳng \(∆\) thì a nằm trong \((P)\) hoặc song song với \((P)\).
Hình vẽ minh họa
Ví dụ: Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng đáy \(\left( {ABC} \right)\). Gọi \(M,N,P\) lần lượt là trọng tâm của ba tam giác \(SAB;SBC;SCA\). Chứng minh rằng: \(SA \bot \left( {MNP} \right)\).
Hướng dẫn giải
Hình vẽ minh họa
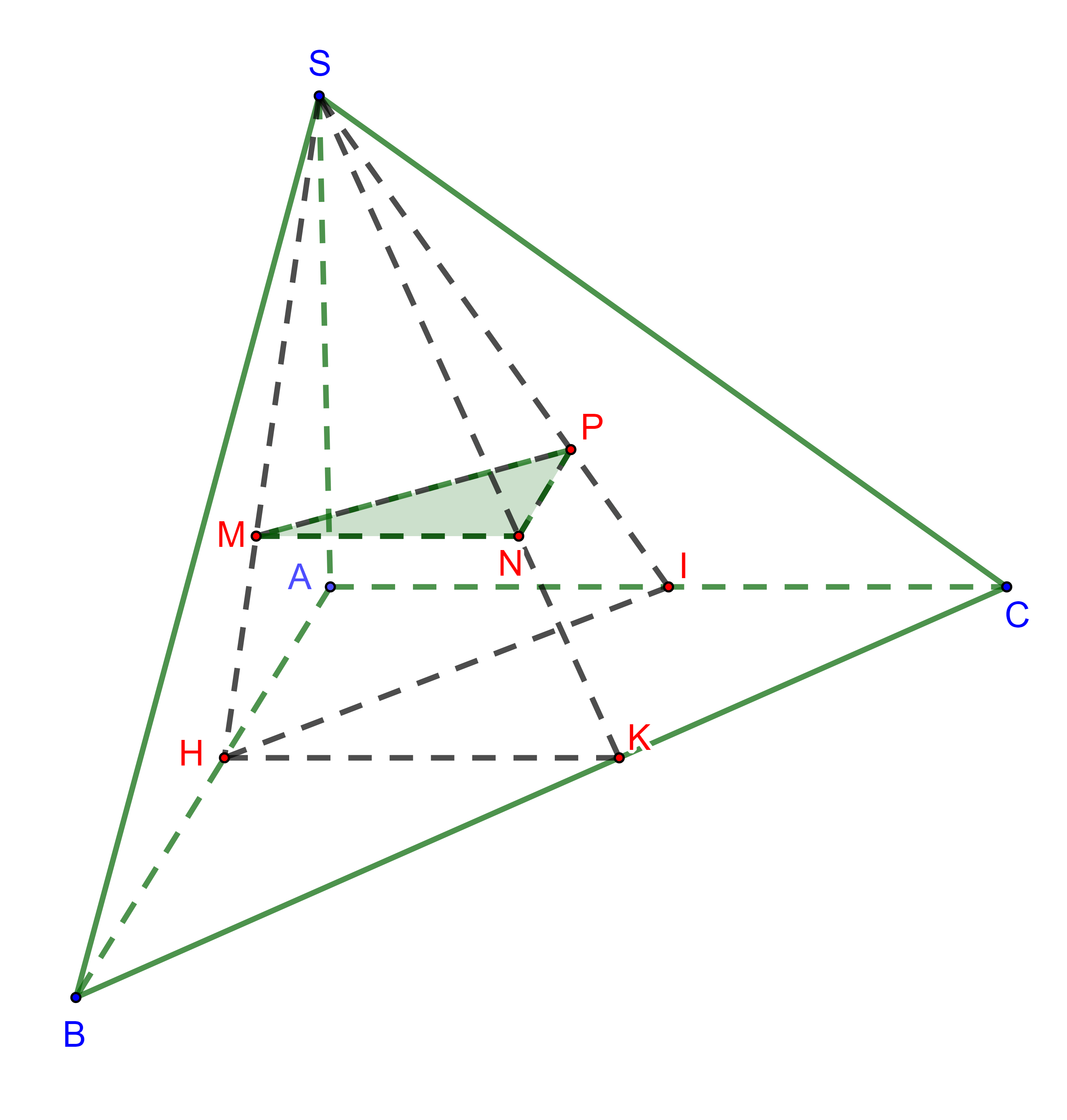
Gọi \(H, I, K\) lần lượt là trung điểm các cạnh \(AB, BC, AC\).
Theo giả thiết ta có: \(\frac{{SM}}{{SH}} = \frac{{SN}}{{SK}} = \frac{{SP}}{{SI}} = \frac{2}{3}\)
Do đó trong tam giác SHK có \(MN//HK\), trong tam giác SHI có \(MP//HI\).
Mà \(\left\{ \begin{gathered}
HK \subset \left( {ABC} \right) \hfill \\
HI \subset \left( {ABC} \right) \hfill \\
\end{gathered} \right.\)
\(\Rightarrow MN//\left( {ABC} \right);MP//\left( {ABC} \right)\)
Ngoài ra, MN và MP cắt nhau trong mặt phẳng (MNP) nê\((MNP) / /(ABC )\).
Mà \(SA \bot \left( {ABC} \right)\)
Vậy \(SA \bot \left( {MNP} \right)\).
